CBSE 12th exams are going on and your Mathematics paper is on 9th March 2024. You have only a few days left for the Mathematics exam.
Therefore, we have introduced students to the best last minute revision tool – the important Topic-Wise Most Important Questions!
This article is for you for CBSE Class 12 Mathematics (Multiple Choice, Assertion-Reason, Case-Based Question, Conceptual Question, Short/Long Question) 4 or 5 marks questions are long answer type questions where students have to answer in the final. A detailed answer with additional information is required to score correctly.
👉 Read Also - CBSE Class 12 Mathematics Exam 2024 : Preparation Tips & Complete Strategy to Score 95+ Marks
The important questions given to you here are essential from the point of view of CBSE Class 12 Board Exam 2024 and hence all the prospective candidates of the exam should practice these questions. We have mentioned all the authentic sources to get the most important questions from each chapter.
👉 Read Also - CBSE Mathematics 12th Exam 2024 : Most Important Chapter-Wise Short Answer Type Questions; Download PDF
In this, every important question has been sorted and collected, which is very important for your paper, so that the student can score good marks in less time. Answers to all the questions are given together.
CBSE Class 12th Mathematics Important Questions 2023-24
Multiple Choice Question
1. A relation R in set A = {1, 2, 3) is defined as R = {(1, 1), (1, 2), (2, 2), (3, 3)). Which of the following ordered pair in R shall be removed to make it an equivalence relation in A?
(a) (1, 1)
(b) (1,2)
(c) (2,2)
(d) (3,3)
Ans. (b) (1,2)
2. Let the relation R in the set A= {xe Z: 0 ≤ x ≤ 12), given R= ((a, b): |a-b is a multiple of 4). Then [1], the equivalence class containing 1, is [CBSE Sample Paper (2021-22) (Term-1)]
(d) A
(a) (1,5,9)
(b) (0,1,2,5)
(c)ø
Ans. (d) A
3. Consider the non-empty set consisting of children in a family and a relation R defined as aRb if a is brother of b, then R is
(a) symmetric but not transitive
(b) transitive but not symmetric
(c) neither symmetric nor transitive
(d) both symmetric and transitive
Ans. (b) transitive but not symmetric
4. The number of equivalence relations in the set {1, 2, 3) containing the elements (1, 2) and (2, 1) is
(a) 0
(b) 1
(c) 2
(d) 3
Ans. (c) 2
5. Let R be a relation on A = {a, b, c) such that R = {(a, a), (b, b), (c, c)}, then R is
(a) Reflexive
(b) Symmetric only
(c) Non-transitive
(d) Equivalence
Ans. (d) Equivalence
6.

Ans. (a)
7.

Ans. (d)
8.

Ans. (b)
9. If A and B are matrices of same order, then (AB' - BA') is a
(a) skew-symmetric matrix
(b) null matrix
(c) symmetric matrix
(d) unit matrix
Ans. (a) skew-symmetric matrix
10.
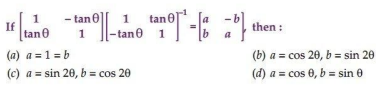
Ans. (b)
11.

Ans. (a)
12.

Ans. (a)
13. The function f(x) = |x|is
(a) continuous and differentiable everywhere.
(b) continuous and differentiable nowhere.
(c) continuous everywhere, but differentiable everywhere except at x = 0.
(d) continuous everywhere, but differentiable nowhere.
Ans. (c) continuous everywhere, but differentiable everywhere except at x = 0.
14. The function f(x) = x|x| is
(a) continuous and differentiable at x = 0.
(b) continuous but not differentiable at x = 0.
(c) differentiable but not continuous at x=0.
(d) neither differentiable nor continuous at x = 0.
Ans. (a) continuous and differentiable at x = 0.
15. The function f: R R given by f(x) = -|r-1| is
(a) continuous as well as differentiable at x = 1
(b) not continuous but differentiable at x = 1
(c) continuous but not differentiable at x = 1
(d) neither continuous nor differentiable at x=1
Ans. (c) continuous but not differentiable at x = 1
16. If x is real, the minimum value of x² - 8x + 17 is
(a) -1
(b) 0
(c) 1
(d) 2
Ans. (c) 1
17. The rate of change of the area of a circle with respect to its radius r at r = 6 cm is
(a) 10л
(b) 12π
(c) 8π
(d) 11л
Ans. (b) 12π
18. A wire of length 20 cm is bent in the form of a sector of a circle. The maximum area that can be enclosed by the wire is:
(a) 20 sq cm
(b) 25 sq cm
(c) 10 sq cm
(d) 30 sq cm
Ans. (b) 25 sq cm
19. The value of b for which the function f(x) = x + cos x + b is strictly decreasing over R is
(a) b<1
(b) No value of b exists
(c) b≤1
(d) b≥1
Ans. (b) No value of b exists
20.
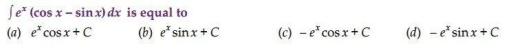
Ans. (a)
21.

Ans. (d)
22.
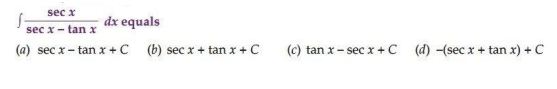
Ans. (b)
23.

Ans. (c)
24. The area of the curve y = sin x between 0 and it is
(a) 2 sq units
(b) 4 sq units
(c) 12 sq units
(d) 14 sq units
Ans. (a) 2 sq units
25. The area of the region bounded by the curves y = x and y = x + 6 and x = 0 is
(a) 7 sq units
(b) 6 sq units
(c) 10 sq units
(d) 14 sq units
Ans. (c) 10 sq units
26. Area of the region bounded by the curve y = cos x between x=0 and x = is
(a) 2 sq units
(b) 4 sq units
(c) 3 sq units
(d) 1 sq unit
Ans. (a) 2 sq units
27.

Ans. (a)
28.

Ans. (d)
29. The co-ordinates of the foot of the perpendicular drawn from the point (2, -3, 4) on the y-axis is
(a) (2, 3, 4)
(b) (-2,-3,-4)
(c) (0, -3, 0)
(d) (2,0,4)
Ans. (c) (0, -3, 0)
30. If the corner points of the feasible region of an LPP are (0,3), (3, 2) and (0,5), then the minimum value of Z = 11x + 7y is
(a) 21
(b) 33
(c) 14
(d) 35
Ans. (a) 21
Assertion-Reason Question
The following questions consist of two statements-Assertion(A) and Reason(R). Answer these questions selecting the appropriate option given below:
(a) Both A and R are true and R is the correct explanation for A.
(b) Both A and R are true but R is not the correct explanation for A.
(c) A is true but R is false.
(d) A is false but R is true.
1. Assertion (A): Let R be the relation on the set of integers Z given by R = ((a, b): 2 divides (a - b)} is an equivalence relation.
Reason (R): A relation R in a set A is said to be an equivalence relation if R is reflexive, symmetric and transitive.
Ans. (a) Both A and R are true and R is the correct explanation for A.
2. Assertion (A): The number of all onto functions from the set (1, 2, 3, 4, 5) to itself is 5!.
Reason (R) Total number of all onto functions from the set (1, 2, 3,...,n) to itself is n!.
Ans. (a) Both A and R are true and R is the correct explanation for A.
3. Assertion (A): Let A = {1, 2, 3) then define a relation on A as R = {(1, 2), (2, 1)), R is not transitive relation.
Reason (R): A relation R defined on a non-empty set A is said to be transitive relation if (a, b), (b, c) eR (a, c) e R.
Ans. (a) Both A and R are true and R is the correct explanation for A.
4. Assertion (A): Function f: R→ R given by f(x) = sin x is not a bijection.
Reason (R): A function f: A → B is said to be bijection if it is one-one and onto.
Ans. (a) Both A and R are true and R is the correct explanation for A.
5. Assertion (A): All trigonometric functions have their inverses over their respective domains.
Reason (R): The inverse of tan¹ x exists for some x = R.
Ans. (c) A is true but R is false.
6. Assertion (A): If A and B are symmetric matrices of same order then AB - BA is also a symmetric matrix.
Reason (R): Any square matrix A is said to be skew-symmetric matrix if A = -AT, where A is the transpose of matrix A.
Ans. (d) A is false but R is true.
7. Assertion (A): Determinant is a number associated with a square matrix.
Reason (R) Determinant is a square matrix.
Ans. (c) A is true but R is false.
8. Assertion (A): If A is an invertible square matrix, then A is invertible.
Reason (R): Inverse of invertible symmetric matrix is a symmetric matrix.
Ans. (b) Both A and R are true but R is not the correct explanation for A.
9.

Ans. (a) Both A and R are true and R is the correct explanation for A.
10.
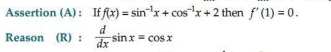
Ans. (d) A is false but R is true.
11.
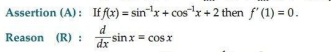
Ans. (b) Both A and R are true but R is not the correct explanation for A.
12. Assertion (A): [sinx | is a continuous function.
Reason (R): If f(x) and g(x) both are continuous functions, then gof(x) is also a continuous function.
Ans. (a) Both A and R are true and R is the correct explanation for A.
13.

Ans. (a) Both A and R are true and R is the correct explanation for A.
14.
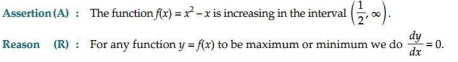
Ans. (b) Both A and R are true but R is not the correct explanation for A.
15.
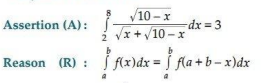
Ans. (a) Both A and R are true and R is the correct explanation for A.
16.
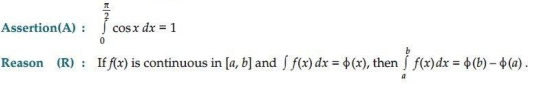
Ans. (a) Both A and R are true and R is the correct explanation for A.
17.
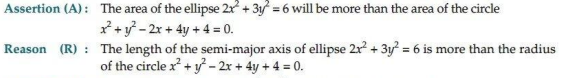
Ans. (b) Both A and R are true but R is not the correct explanation for A.
18.
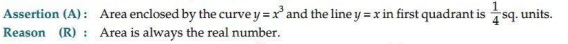
Ans. (b) Both A and R are true but R is not the correct explanation for A.
19.

Ans. (b) Both A and R are true but R is not the correct explanation for A.
20.
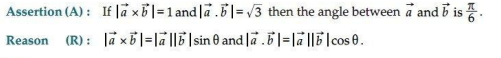
Ans. (a) Both A and R are true and R is the correct explanation for A.
Case-Based Question
1.

Ans.

2.
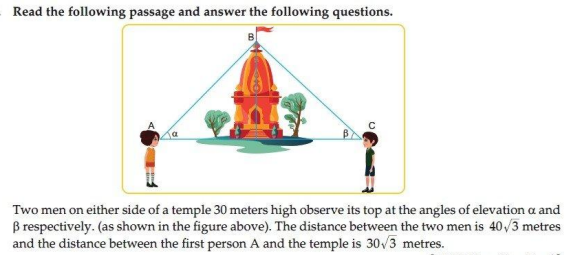

Ans.

3.
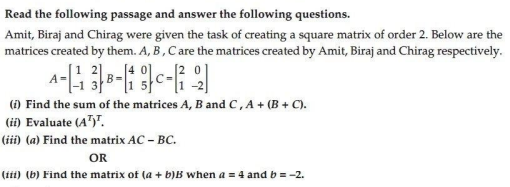
Ans.

4.

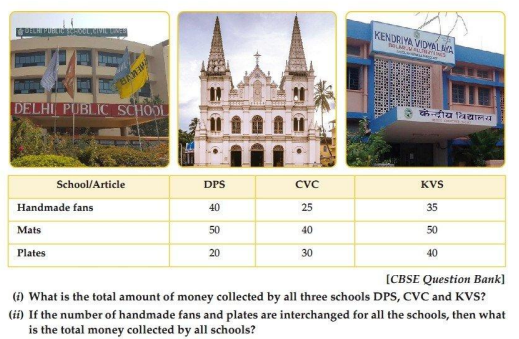
Ans.
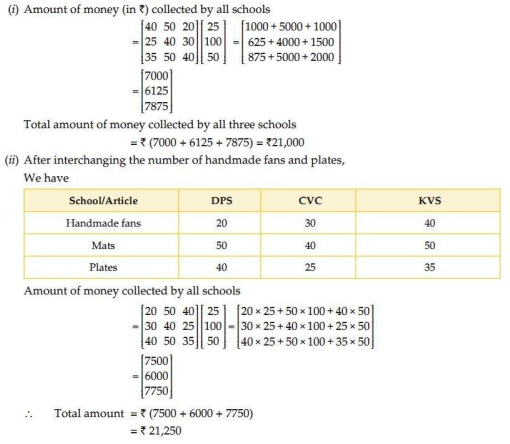
5.

Ans.

6.
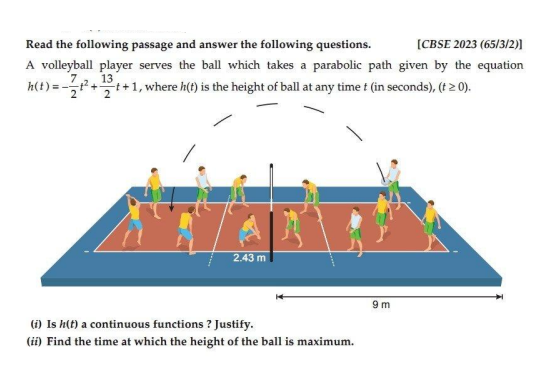
Ans.

7.


Ans.

8.
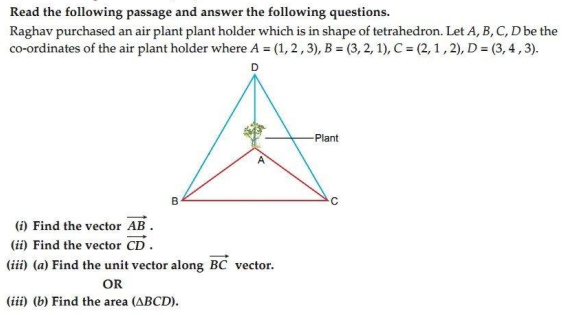
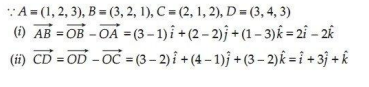
Ans.

9.
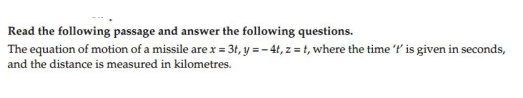

Ans.

10.

Ans.

Very Short Answer Question
1. A function f: A → B defined as f(x) = 2x is both one-one and onto. If A = {1, 2, 3, 4), then find the set B.
Ans. Given a function f: A → B defined as f(x) = 2x is both one-one and onto.
if A = {1, 2, 3, 4)
f(1) = 2x1=2, f(2) = 2 x 2 = 4, f(3) = 2 x 3 = 6 and f(4) = 2x4 = 8
B = (2, 4, 6, 8)
2. Write the inverse relation corresponding to the relation R given by R = {(x, y): xe N, x <5, y = 3). Also write the domain and range of inverse relation.
Ans. Given, R= {(x, y): xe N, x<5,y=3}
=> R={(1, 3), (2, 3), (3, 3), (4, 3)}
Hence, required inverse relation is
R-1= ((3, 1), (3, 2), (3, 3), (3, 4))
.. Domain of R-¹= (3) and
Range of R-¹ = {1, 2, 3, 4)
3.
Ans.
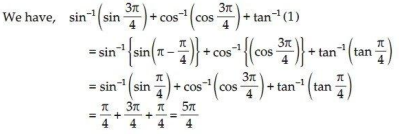
4.
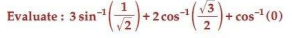
Ans.
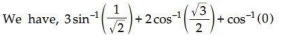
5.
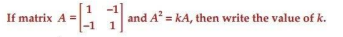
Ans.
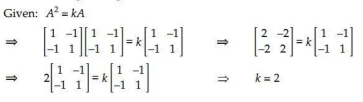
6.
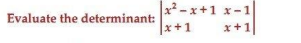
Ans.
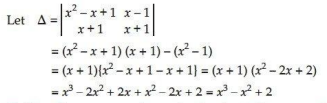
7.
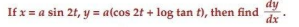
Ans.
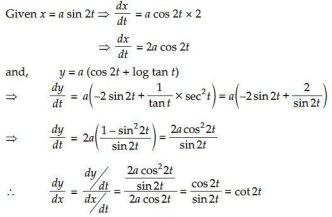
8.
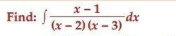
Ans.
9.

Ans.
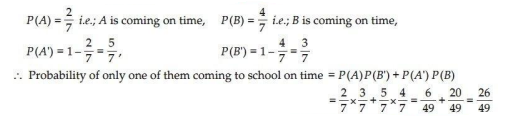
10.

Ans.

Long Answer Question
1.

Ans.

2.

Ans.

3.
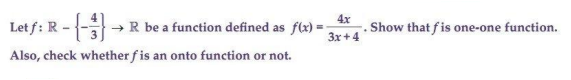
Ans.

4.

Ans.

5.

Ans.

6. Sum of two numbers is 5. If the sum of the cubes of these numbers is least, then find the sum of the squares of these numbers.
Ans.

7.

Ans.
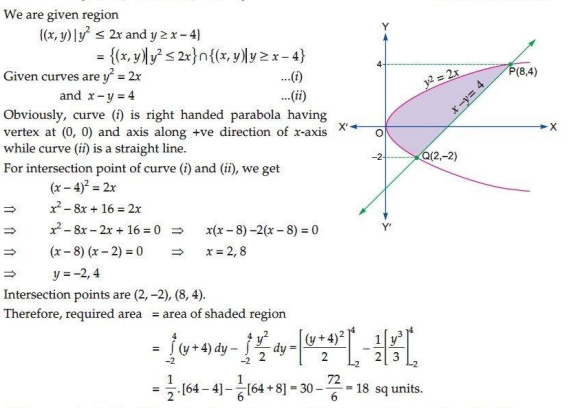
8.

Ans.

9.
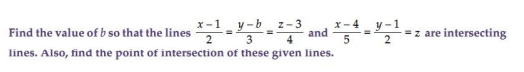
Ans.

10. There are three coins. One is two headed coin (having head on both faces), another is a biased coin that comes up head 75% of the times and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin?
Ans.

Read Also
CBSE Class 10 & 12 Exam 2024: Last-Minute Preparation Tips to Help You Secure High Score
Don't Follow These Fake Social Media Handles During 2024 Board Exams – CBSE Shares List
CBSE 10th, 12th Exam 2024 : 30 Days Study Plan & Day Wise Study Schedule; Check Here
CBSE Board Class 10, 12 Exam 2024 : Common Writing Mistakes, Students Must Avoid For High Scores
Read Also -
CBSE Physics 12th Exam 2024 : Most Important Chapter-Wise Short Answer Type Questions; Download PDF
CBSE Biology 12th Exam 2024 : Most Important Chapter-Wise Short Answer Type Questions; Download PDF
CBSE Class 12 Study Materials
| CBSE Class 12 Syllabus 2023-24 | CBSE Class 12 Previous Year Papers |
| NCERT Books For Class 12 Books | NCERT Class 12 Solutions |
| CBSE Class 12 Full Study Material | CBSE Class 12 Sample Paper 2023-24 |
--







 Profile
Profile Signout
Signout








 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










