As the CBSE Class 12 board exams get closer, it’s important for students to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.
This article explores Chapter 3 Matrices It highlights key competency-based questions and provides answers to help students succeed.
Understanding Competency-Based Questions in Chapter 3 Matrices
Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.
These questions are different from regular memorization. They encourage students to think critically and solve problems, helping them understand the concepts in Chapter 3 Matrices better.
CBSE Class 12 Maths Chapter 3 Matrices Important Competency-Based Questions
Q.1
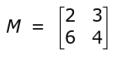
Given below are two statements in relation with the above matrix- one labelled Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
Assertion (A) : The matrix M cannot be expressed as the sum of a symmetric and a skew-symmetric matrix.
Reason (R) : The matrix M is neither a symmetric matrix nor a skew-symmetric matrix.
1. Both (A) and (R) are true and (R) is the correct explanation for (A).
2. Both (A) and (R) are true but (R) is not the correct explanation for (A).
3. (A) is false but (R) is true.
4. Both (A) and (R) are false.
Answer. 3
Q.2 The following are two non-zero matrices M and N:
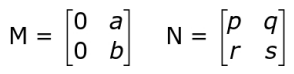
What is the necessary condition for their product to be a zero matrix? Show your work and give valid reason.
Answer. Writes the product of the matrices M and N as follows:
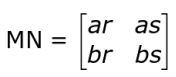
Writes that the necessary condition for MN to be a zero matrix is that the values of r 0.5 and s must always be 0 because a and b cannot be zero as M is a non-zero matrix.
Q.3 Shown below is matrix P.
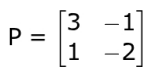
Find one such matrix Q such that (P + Q) is a skew-symmetric matrix. Show your work.
Answer. Represents the matrix (P + Q) as shown below:
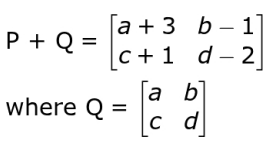
Uses the skew-symmetric relation (P + Q) = -(P + Q)' to write the equation as:
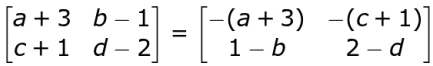
Finds the value of a as (-3), d as 2 and the relation b = - c using the equality of 1 matrices in the above step and solve the following equations:
a + 3 = -( a + 3)
d - 2 = 2 - d
and
b - 1 = -( c + 1)
Finds the matrix Q as shown below where the numerical values of b and c are such 0.5 that c = - b :
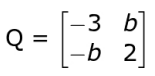
| Download PDF | |
| CBSE Class 12 Maths Chapter 1: Relations and Functions Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 2 : Inverse Trigonometric Functions Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 3 : Matrices Important Competency-Based Questions | Click Here |
Q.4 Drona is solving a bank robbery. He has a note from one of his informants, Arjun, which contains the robber's name in the form of an encoded matrix N.
♦ The decoded name is stored in the form of a matrix M with numbers representing letters, such that 1 = A, 2 = B, 3 = C, and so on until 26 = Z.
♦ The entries are to be read column-wise.
♦ Arjun's notes to Drona are encoded using an encoder matrix, E.
♦ Matrix E is multiplied with Matrix M, to get the matrix in the note, N.
Matrices N and E are given below.
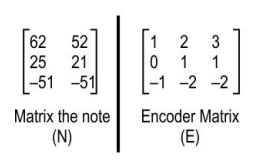
Find the key to decode the matrix N, and use it to find the robber's name. Show your work.
Answer. Notes that the determinant of Matrix E ≠ 0.
Writes that, since EM = N, we can multiply both sides by E -1 to get E -1 EM = E -1 N. Simplifies the above expression to get M = E -1 N.
Finds the inverse of matrix E using elementary row operations.
The solution may look as follows:
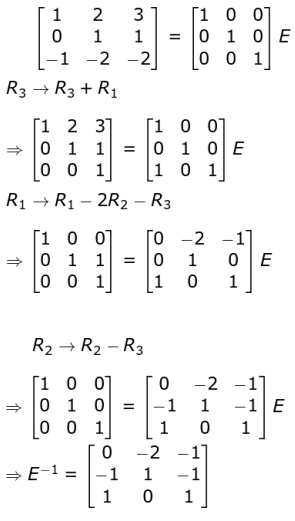
(Award full marks if inverse is found using adj(E) ÷ det(E). )
Multiplies E 1.5 -1 with N as follows to get M:
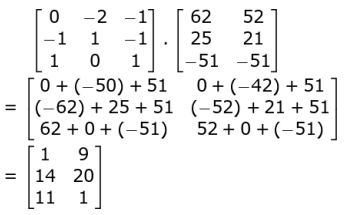
Decodes the letters representing the numbers and reads them column-wise to g the robber's name as ANKITA.
Q.5 As part of an architecture project, Henry needs to create a miniature model of the Clifton Bridge, located in Bristol, UK. In order to do this, he must first find the equation of a parabola equivalent to the one made in Clifton Bridge.
He found a picture of the Clifton bridge, and placed it on a coordinate grid, as shown below. He noted that the parabola crossed the points (10, 3), (26, 3) and (30, 4) on the grid.
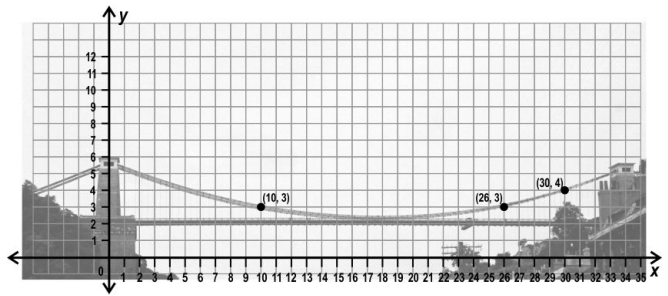
If the required parabola is of the form y = ax 2 + bx + c , then help Henry by finding a, b and c, and hence finding the equation of the parabola. Show your work.
Answer. Writes the system of equations as:
0.5 100 a + 10 b + c = 3
676 a + 26 b + c = 3
900 a + 30 b + c = 4
Writes the above system of equations in the form AX = B as follows:
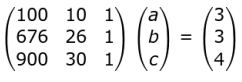
Finds |A| as 1(20280 - 23400) - 1(3000 - 9000) + 1(2600 - 6760) = -1280. Writes that A -1 exists as |A| ≠ 0.
Finds A 2 -1 as:
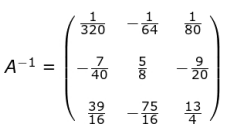
(Award 1 mark if only all the cofactors are found correctly.)
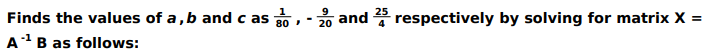
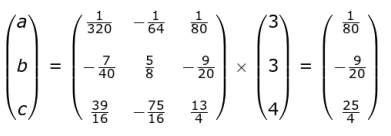
Writes that the equation of a parabola equivalent to that of the Clifton bridge is
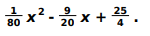
Q.6 T is a matrix given by:
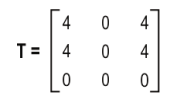
On performing which of the following individual operations, will the matrix T remain the same?
i) C₁→ C3
ii) R₂→ R₂+99R3
iii) C₂ → (-1)C₂
1. only (i) and (ii)
2. only (ii) and (iii)
3. only (i) and (iii)
4. all (i), (ii) and (iii)
Answer. 4
Q.7 A teacher gave the following problem to his students.
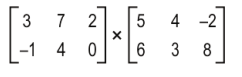
Three students' solutions are shown below.
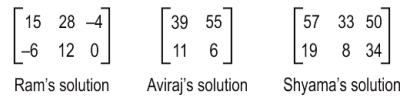
Who gave the correct answer?
1. only Ram
2. only Aviraj
3. only Shyama
4. none of them
Answer. 4
Q.8
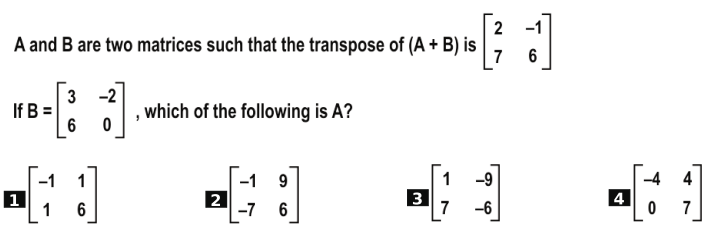
Answer. 2
Q. 9 In an online advertisement (ad) campaign, there are two options for publicity: picture ads and video ads.
The cost per ad (in Rs) is given by the matrix:

The number of ads run by two companies X and Y is given by the matrix:

To find the total cost of ads for the two companies, Nahush performs the matrix operation A x B while Divyesh performs the matrix operation B x A. Who is correct?
1. Only Nahush
3. Both Nahush and Divyesh
2. Only Divyesh
4. Neither Nahush nor Divyesh
Answer. 2
Q.10 A and B are two matrices such that both products, AB and BA, exist.
Write a condition on the order of the matrices A and B for the above statement to be true.
Answer. Writes that the above statement will be true if the orders of matrices A and B are of the form m x n and n x m respectively, where m and n are positive integers.
(Award 0.5 marks if the condition 'both the matrices A and B are square matrices of the same order' is written.)
OR
(Award 0.5 marks if particular orders are written instead. For example, 2 x 3 and 3 x 2.)
Q.11 Identify if the statement below is true or false. If true, give a reason. If false, give a counter-example.
"If A is a non-zero matrix such that A x K is a zero matrix, then K is definitely a zero matrix."
Answer. Writes False(F).
Gives a counterexample. For example:
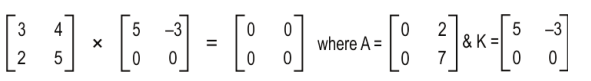
Q.12 A is a 4 x 3 matrix, which when multiplied by matrix B, results in a 4 x 2 matrix, C.
How many rows and columns does matrix B have? Justify your answer.
Answer. Writes that B has 3 rows and 2 columns.
Gives reason that, since A is a 4 x 3 matrix, B must have 3 rows. Further, since the product C is a 4 x 2 matrix, B must have 2 columns.
Q.13 If B is a symmetric matrix, prove that BB' is a symmetric matrix.
Answer. Writes that, since B is a symmetric matrix, B = B'.
Proves that BB' is a symmetric matrix as:
(BB')' (B')' x B' = BB'
(Award 0.5 marks if only an example is written instead of a proof.)
Q.14 D is a matrix of order 3 which is both symmetric and skew symmetric.
Find D. Show your work.
Answer. Writes that D' = D as D is a symmetric matrix.
Writes that D' = -D as D is a skew symmetric matrix.
Uses the above steps to conclude that D is a null matrix of order 3. The working may look as follows:
D = -D
⇒ 2D = 0
⇒ D = 0
(Award 0.5 marks if the correct conclusion is written without any working.)
Q. 15 5 K1, is the new key matrix obtained by performing the elementary row operation R₂-> R₂+ R1 on K, where R1, and R2, denote rows 1 and 2 respectively.
Find K₁'
Answer.
Finds K, as:
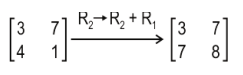
----
👉 Read Also - CBSE Class 12 Half-Yearly/Mid Term 2024-25 : Most Important Questions with Answers; PDF Download (All Subjects)
👉 Read Also - How CBSE’s New Exam Pattern Will Impact Class 11 and 12 Students
👉 CBSE Class 12 Study Materials
| CBSE Class 12 Syllabus 2024-25 | CBSE Class 12 Previous Year Papers |
| NCERT Books For Class 12 Books | NCERT Class 12 Solutions |
| CBSE Class 12 Full Study Material | CBSE Class 12 Sample Paper 2023-24 |







 Profile
Profile Signout
Signout








 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










