CBSE Class 12 Maths 2025: Top 50 MCQs with Answers for Last-Minute Revision

CBSE 12th exams are underway and your CBSE 12th Maths exam is scheduled for 8th march, 2025. You have just a few hours left for CBSE 12th Maths exam.

We have prepared Top 50 MCQs with answers covering all the important topics of CBSE Class 12 Maths syllabus.

Make sure to solve these MCQs and refer to the solutions to ensure that you are well prepared to score high in CBSE Class 12 Maths exam 2025.

CBSE 12th Maths 2025: Top 50 MCQs with Answers

1.Let A = {1, 2, 3} and consider the relation R = {1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1,3)}. Then R is

(a) reflexive but not symmetric

(b) reflexive but not transitive

(d) neither symmetric, nor transitive

Answer - (b) Reflexive but not transitive

2. The function f : R → R defined by f(x) = 3 – 4x is

(a) Onto

(b) Not onto

(d) None of these

Answer - (a) Onto

3. How many distinct relations can be defined on the set A = {1,2,3}?

(a) 29

(b) 23

(d) 26

Answer - (a) 2⁹ = 512

4. If f: R → R be given by f(x) = (3 – x3)1/3, then fof(x) is

(a) x1/3

(b) x3

(d) (3 – x3)

Answer - (c) x

5. Which of the following is the principal value of sin-1(1)?

a) π/2

b) π/4

c) π

c) 0

Answer - (a) π/2

👉 CBSE Class 12 Study Materials

CBSE Class 12 Syllabus 2024-25	CBSE Class 12 Previous Year Papers
NCERT Books For Class 12 Books	NCERT Class 12 Solutions
CBSE Class 12 Full Study Material	CBSE Class 12 Sample Paper 2024-25

6. The domain of the function f(x) = sin-1(x) is:

a) [-1, 1]

b) (-∞, ∞)

c) [0, 1]

c) [0, π/2]

Answer - (a) [-1, 1]

7. The value of tan-1(√3) is:

a) π/4

b) π/3

c) π/6

c) 2π/3

Answer - (b) π/3

8. The value of sin(cos-1(1/2)) is:

a) √3/2

b) 1/√3

c) 2/√3

c) 1/2

Answer - (d) 1/2

9. Matrices A and B will be inverse of each other only if:

(a) AB = BA

(b) AB-BA = 0

(d) AB = BA = I

Answer - (d) AB = BA = I

10. If A and B are two matrices of the order 3 × m and 3 × n, respectively, and m = n, then the order of matrix (5A – 2B) is

(a) m x 3

(b) 3 x 3

(d) 3 x n

Answer - (d) 3 × n

11. Which of the following is correct?

(a) Determinant is a square matrix.

(b) Determinant is a number associated with a matrix.

(d) None of these

Answer - (c) Determinant is a number associated with a square matrix

12. If A is an invertible matrix of order 2, then det (A–1) is equal to

(a) det (A)

(b) 1/det (A)

(d) 0

Answer -(b) 1/det(A)

13. The function f(x) = [ln(1+ax)-ln(1-bx)]/x, not defined at x=0. The value should be assigned to f at x=0, so that it is continuous at x =0, is

(a) a+b

(b) a-b

(d) ln a+ ln b

Answer -(b) a - b

14. If x sin(a+y) = sin y, then dy/dx is equal to

(a) [sin²(a+y)]/sin a

(b) sin a /[sin²(a+y)]

(d) sin a /[sin(a+y)]

Answer - (b) sin a / sin²(a + y)

14. The value of c in Rolle’s theorem for the function, f(x) = sin 2x in [0, π/2] is

(a) π/4

(b) π/6

(d) π/3

Answer - (a) π/4

15. If f(x) = 3x⁴ - 4x² + 5, then the interval for which f(x) satisfy all the conditions of Rolle’s theorem, is

(a) (0, 2)
(b) (-1, 1)
(c) (-1, 0)
(d) (-1, 2)

Answer -(b) (-1,1)

16. The function f(x) = x⁵ – 5x⁴ + 5x³ – 1 has

(a) one minima and two maxima

(b) two minima and one maxima

(d) one minima and one maxima

Answer -(a) One minima and two maxima

17. If x increases at the rate of 2 m/sec at the instant when x = 3 m, y = 1 m, at what rate must y be changing in order that the function 2xy - 3x²y shall be neither increasing nor decreasing?

(a) 32/21 m/sec; increasing

(b) 32/21 m/sec; decreasing

(d) 8/21 m/sec; decreasing

Answer -(b) 32/21 m/sec; decreasing

18. ∫ 2^x dx = f(x) + C, then f(x) is

(a) 2^x

(b) 2^xlog_e2

(d) 2^x+1/x+1

Answer -(c) 2x / logₑ2

19. f a is such that ₀∫^a x d x ≤ a + 4, then

(a) 0 ≤ a ≤ 4

(b) -2 ≤ a ≤ 0

(d) -2 ≤ a ≤ 4

Answer -(d) -2 ≤ a ≤ 4

20. If ∫dx/[(x+2)(x²+1)] = a log |1 + x²| + b tan–1x + (1/5) log |x + 2| + C, then

(a) a = -1/10, b = -2/5

(b) a = 1/10, b = -2/5

(d) a = 1/10, b = 2/5

Answer -(c) a = -1/10, b = 2/5

21. The area of the region bounded by the curve x² = 4y and the straight line x = 4y – 2 is

(a) 3/8 sq. units

(b) 5/8 sq. units

(d) 9/8 sq. units

Answer -

22. The area of the region bounded by the curve y = √16-x² and x-axis is

(a) 8π sq. units

(b) 20π sq. units

(d) 256 sq. units

Answer -(c) 16π sq. units

23. The area bounded by the lines y = |x| - 1 and y = -|x| + 1 is

(a) 1 sq. unit

(b) 2 sq. unit

(d) 4 sq. unit

Answer - (b) 2 sq. unit

24. The area bounded by the curves y=cosx, y=sinx, Y-axis and 0⩽x ⩽π/4 is _____ .

(a) 2(√2-1)

(b) √2-1

(d) √2

Answer - (b) √2 - 1

25. Solution of differential equation xdy – ydx = Q represents

(a) a rectangular hyperbola

(b) parabola whose vertex is at origin

(d) a circle whose centre is at origin

Answer - (c) Straight line passing through origin

26. What is the degree of differential equation (y’’’)² + (y’’)³ + (y’)⁴+ y⁵= 0?

(a) 2

(b) 3

(d) 5

Answer - (c) 4

27. The solution of (x+ logy)dy +ydx =0 where y(0) =1 is

(a) y(x−(A)) + ylogy = 0

(b) y(x−1+logy) + 1 = 0

(d) None of these

Answer - (c) xy + y log y + 1 = 0

28. What is the differential equation of the family of circles touching the y-axis at the origin?

(a) 2xyy’ + x² = y²

(b) 2xyy’’ + x’ = y²

(d) xyy’ + x² = y²

Answer - (c) 2xyy' - x² = y²

29. The scalar product of 5i + j – 3k and 3i – 4j + 7k is:

(a) 15

(b) -15

(d) -10

Answer - (b) -15

30. The magnitude of the vector 6i + 2j + 3k is equal to:

(a) 5

(b) 1

(d) 12

Answer - (c) 7

30. If vectors |A.B|=|A×B|, then angle between A and B is

(a) 60^o

(b) 30^o

(d) 45^o

Answer - (c) 90°

31.

Answer -

32.

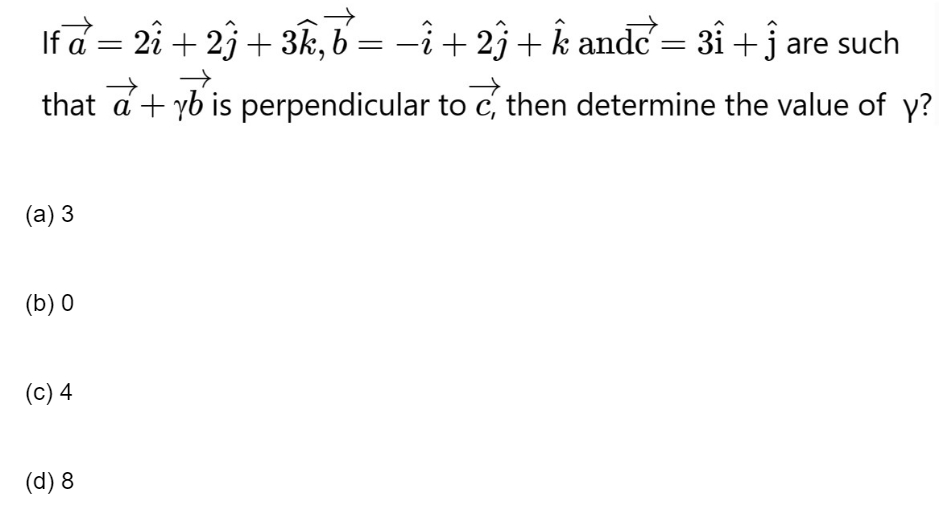Answer -

33. If the direction cosines of a line are k/3,k/3,k/3, then value of k is

(a) k > 0

(b) 0 < k < 1.

(d) k = ±3

Answer - (d) k = ±3

34. Find the equation of the plane passing through the points P(1, 1, 1), Q(3, -1, 2), R(-3, 5, -4).

(a) x + 2y = 0

(b) x – y – 2 = 0

(d) x + y – 2 = 0

Answer - (c) -x + 2y - 2 = 0

35. The vector equation for the line passing through the points (–1, 0, 2) and (3, 4, 6) is:

(a) i +2k + λ(4i + 4j + 4k)

(b) i –2k + λ(4i + 4j + 4k)

(d) -i+2k+ λ(4i – 4j – 4k)

Answer - (c) -i + 2k + λ(4i + 4j + 4k)

36. If l, m, n are the direction cosines of a line, then;

(a) l²+ m²+ 2n² = 1

(b) l²+ 2m2+ n² = 1

(d) l²+ m²+ n² = 1

Answer - (d) l² + m² + n² = 1

37. If a line has direction ratios 2, – 1, – 2, determine its direction cosines:

(a) ⅓, ⅔, -⅓

(b) ⅔, -⅓, -⅔

(d) None of the above

Answer - (b) ⅔, -⅓, -⅔

38. Maximize Z = 3x + 5y, subject to constraints: x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0

(a) 20 at (1, 0)

(b) 30 at (0, 6)

(d) 33 at (6, 3)

Answer - (c) 37 at (4,5)

39. Minimize Z = 20x1 + 9x2, subject to x1 ≥ 0, x2 ≥ 0, 2x1 + 2x2 ≥ 36, 6x1 + x2 ≥ 60.

(a) 360 at (18, 0)

(b) 336 at (6, 4)

(d) 0 at (0, 0)

Answer - (b) 336 at (6,4)

40. In solving the LPP: minimize f = 6x + 10y subject to constraints x ≥ 6, y ≥ 2, 2x + y ≥ 10, x ≥ 0, y ≥ 0 redundant constraints are

(a) x ≥ 6

(b) 2x + y ≥ 10, x ≥ 0, y ≥ 0

(d) None of these

Answer - (c) x ≥ 6, y ≥ 2

41. The maximum value of Z = 3x + 4y subjected to constraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0, y ≥ 0 is

(a) 130

(b) 120

(d) 140

Answer - (b) 120

42. Find P(E|F), where E: no tail appears, F: no head appears when two coins are tossed in the air.

(a) 0

(b) ½

(d) None of the above

Answer - (a) 0

43. If P(a) = 0,4, P(b) = 0.8 and P(B|A) = 0.6 then P(A∪B) is equal to

(a) 0.24

(b) 0.3

(d) 0.96

Answer - (d) 0.96

44. If A and B are two independent events, then the probability of occurrence of at least one of A and B is given by:

(a) 1+ P(A′) P (B′)

(b) 1− P(A′) P (B′)

(d) 1− P(A′) – P (B′)

Answer - (b) 1 - P(A') P(B')

45. If P(A ∩ B) = 70% and P(B) = 85%, then P(A/B) is equal to:

(a) 17/14

(b) 14/17

(d) ⅛

Answer - (b) 14/17

46. A person writes 4 letters and addresses 4 envelopes. If the letters are placed in the envelopes at random, then the probability that all letters are not placed in the right envelopes, is

(a) 23/24

(b) 15/24

(d) 1/4

Answer - (a) 23/24

47. If E and F are independent events, then;

(a) P(E ∩ F) = P(E)/ P(F)

(b) P(E ∩ F) = P(E) + P(F)

(d) None of the above

Answer - (c) P(E ∩ F) = P(E) * P(F)

48. A police officer fires three bullets at a thief. The probability that the thief will be killed by one bullet is 0.8. Find the probability of the thief being still alive?

(a) 0.008

(b) 0.0016

(d) None of the above

Answer - (b) 0.0016

49. The mean and the variance of a binomial distribution are 4 and 2 respectively. Then the probability of 2 success is

(a) 28/256

(b) 219/256

(d) 37/256

Answer - (a) 28/256

50. The probability of a student getting 1, 2, 3 division in an examination are 1/10, 3/5 and 1/4 respectively. The probability that the student fails in the examination is

(a) 27/100

(b) 83/100

(d) 197/200

Answer - (a) 27/100