The CBSE Class 12 pre-board exams for 2024-25 are an important step in your exam preparation. These exams help you check how well you’re prepared for the final board exams.
To help you study better, we’ve created a list of the most important Mathematics questions with answers. This Maths question focuses on essential topics to help you perform well.
The CBSE Pre-board Exam Mathematics questions cover key topics. They include objective, short/long answer, and competency-based questions, all matching the latest exam pattern.
👉 Read Also - CBSE Class 12 Pre-Board Exam 2024-25: Chemistry Important Questions with Answers – Free PDF Download
👉 Read Also - CBSE Class 12 Pre-Board Exam 2024-25: Biology Important Questions with Answers – Free PDF Download
👉 Read Also - CBSE Class 12 Pre-Board Exam 2024-25: Physics Most Important Questions with Answers – Free PDF Download
CBSE 12 Pre-board Exam 2024-25 Maths Most Important Questions
1. A function f : R+ → R (where R+ is the set of all non-negative real numbers) defined by f(x) = 4x + 3 is :
(A) one-one but not onto
(B) onto but not one-one
(C) both one-one and onto
(D) neither one-one nor onto
Ans. (A) one-one but not onto
2. If a matrix has 36 elements, the number of possible orders it can have, is :
(A) 13
(B) 3
(C) 5
(D) 9
Ans. (D) 9
3. Which of the following statements is true for the function
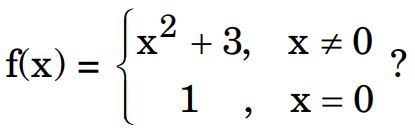
(A) f(x) is continuous and differentiable ∀ x ∈ ℝ
(B) f(x) is continuous ∀ x ∈ ℝ
(C) f(x) is continuous and differentiable ∀ x ∈ ℝ – {0}
(D) f(x) is discontinuous at infinitely many points
Ans. (C) f(x) is continuous and differentiable ∀ x ∈ ℝ – {0}
| Download PDF | |
| CBSE 12 Pre-board Exam 2024-25 Mathematics Most Important Questions | Click Here |
4. Let f(x) be a continuous function on [a, b] and differentiable on (a, b). Then, this function f(x) is strictly increasing in (a, b) if
(A) f'(x) < 0, ∀ x ∈ (a, b)
(B) f'(x) > 0, ∀ x ∈ (a, b)
(C) f'(x) = 0, ∀ x ∈ (a, b)
(D) f(x) > 0, ∀ x ∈ (a, b)
Ans. (B) f'(x) > 0, ∀ x ∈ (a, b)
5.
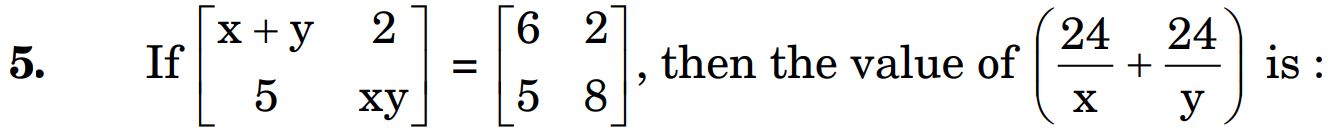
(A) 7
(B) 6
(C) 8
(D) 18
Ans. (D) 18
6.
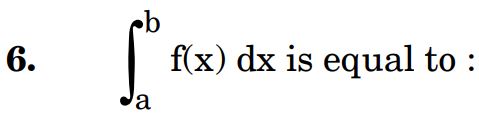

Ans. (b)
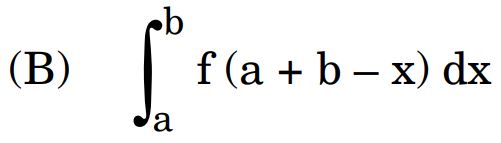
7.


Ans.
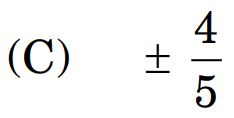
8. The integrating factor of the differential equation (1 – x2) dy/dx + xy = ax, – 1 < x < 1, is :

Ans.
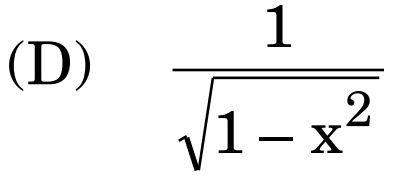
9. If the direction cosines of a line are √3k, √3k, √3k, then the value of k is :

Ans.
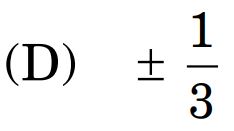
10. A linear programming problem deals with the optimization of a/an :
(A) logarithmic function
(B) linear function
(C) quadratic function
(D) exponential function
Ans. (B) linear function
11. If P(A|B) = P(A'|B), then which of the following statements is true ?
(A) P(A) = P(A')
(B) P(A) = 2 P(B)
(C) P(A ∩ B) = 1/2 P(B)
(D) P(A ∩ B) = 2 P(B)
Ans. (C) P(A ∩ B) = 1/2 P(B)
12.
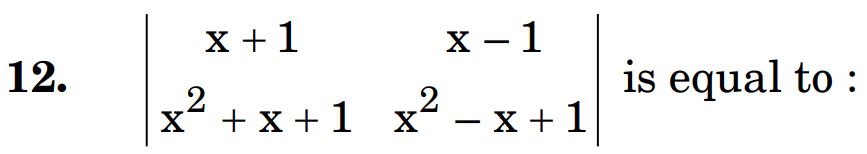
(A) 2x3
(B) 2
(C) 0
(D) 2x3 – 2
Ans. (B) 2
13. The derivative of sin (x2) w.r.t. x, at x = √Π is :
(A) 1
(B) – 1
(C) – 2 √Π
(D) 2 √Π
Ans. (C) – 2 √Π
14. The order and degree of the differential equation
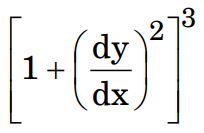
= d2y/dx2 respectively are :
(A) 1, 2
(B) 2, 3
(C) 2, 1
(D) 2, 6
Ans. (C) 2, 1
15. The vector with terminal point A (2, – 3, 5) and initial point B (3, – 4, 7) is :

Ans.
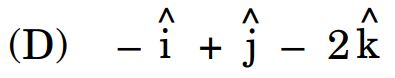
16. The distance of point P(a, b, c) from y-axis is :

Ans.
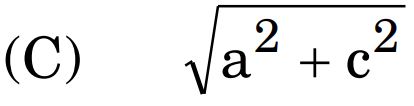
17. The number of corner points of the feasible region determined by constraints x ≥ 0, y ≥ 0, x + y ≥ 4 is :
(A) 0
(B) 1
(C) 2
(D) 3
Ans. (C) 2
18. If A and B are two non-zero square matrices of same order such that (A + B)2 = A2 + B2, then :
(A) AB = O
(B) AB = – BA
(C) BA = O
(D) AB = BA
Ans. (B) AB = – BA
Questions number 19 and 20 are Assertion and Reason based questions. Two statements are given, one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer from the codes (A), (B), (C) and (D) as given below.
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
(B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
(C) Assertion (A) is true, but Reason (R) is false.
(D) Assertion (A) is false, but Reason (R) is true.
19. Assertion (A) : For matrix A =
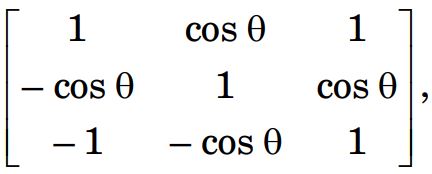
where θ ∊ [0, 2Π], |A| ∊ [2, 4].
Reason (R) : cos θ ∊ [– 1, 1], ∀ θ ∊ [0, 2Π].
Ans. (A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
20. Assertion (A) : A line in space cannot be drawn perpendicular to x, y and z axes simultaneously.
Reason (R) : For any line making angles, α, β, γ with the positive directions of x, y and z axes respectively, cos2 α + cos2 β + cos2 γ = 1.
Ans. (A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
21. (a) Check whether the function f(x) = x2 |x| is differentiable at x = 0 or not.
Ans.
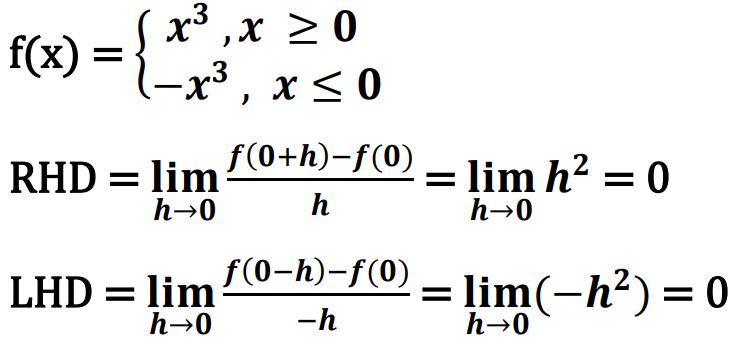
∵ 𝑹𝑯𝑫 = 𝑳𝑯𝑫 = 𝟎, 𝑺𝒐 𝒇(𝒙) 𝒊𝒔 𝒅𝒊𝒇𝒇𝒆𝒓𝒆𝒏𝒕𝒊𝒂𝒃𝒍𝒆 𝒂𝒕 𝒙 = 0
OR
21. (b)
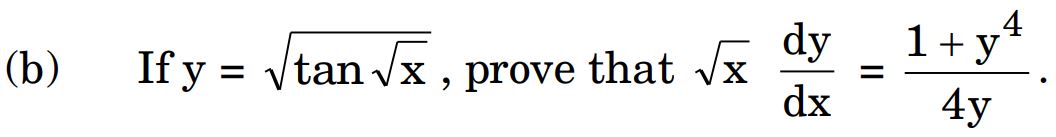
Ans.
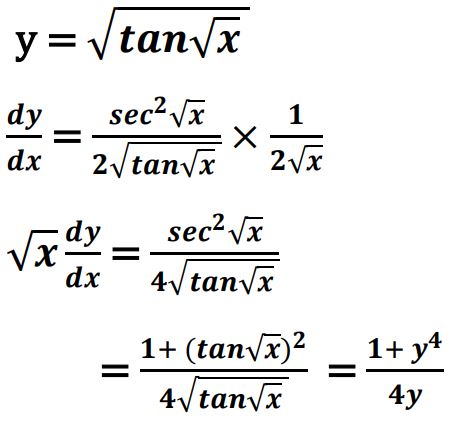
22. Show that the function f(x) = 4𝒙3 – 18𝒙2 + 27𝒙 – 7 has neither maxima nor minima.
Ans. f′ (x) = 12𝒙2 − 36𝒙 + 27
= 3 (2 x -3)2 ≥ 0 for all 𝒙 ∈ R
∴ f is increasing on R .
Hence f(x) does not have maxima or minima.
23. (a) Find :
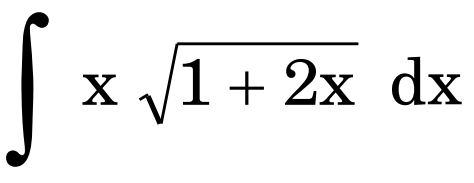
Ans. 1 + 2𝒙 = 𝒕𝟐
2 𝒅𝒙 = 2𝒕 𝒅𝒕
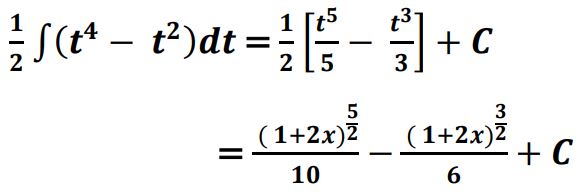
OR
(b) Evaluate :
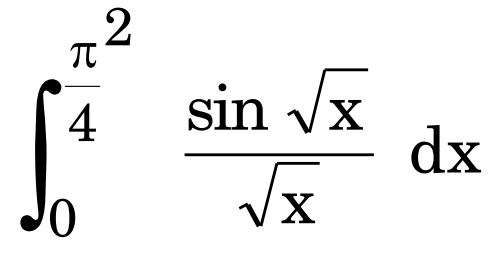
Ans.
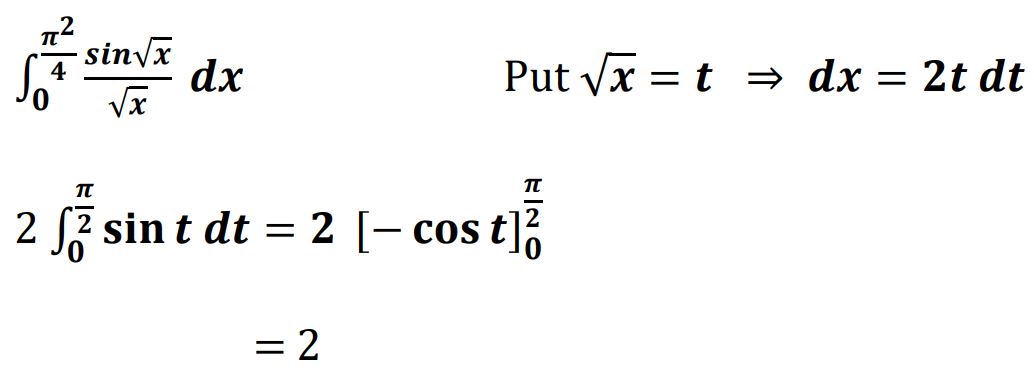
24.
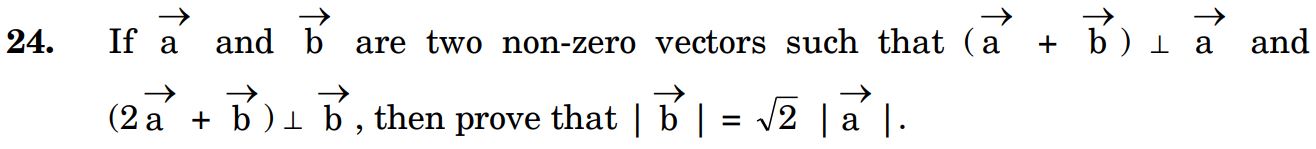
Ans.
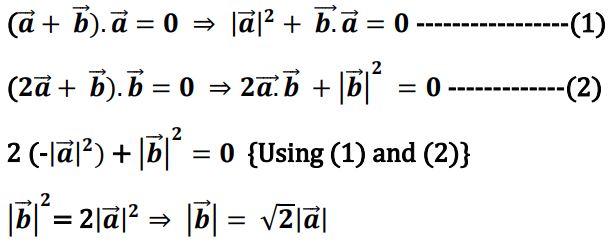
25.
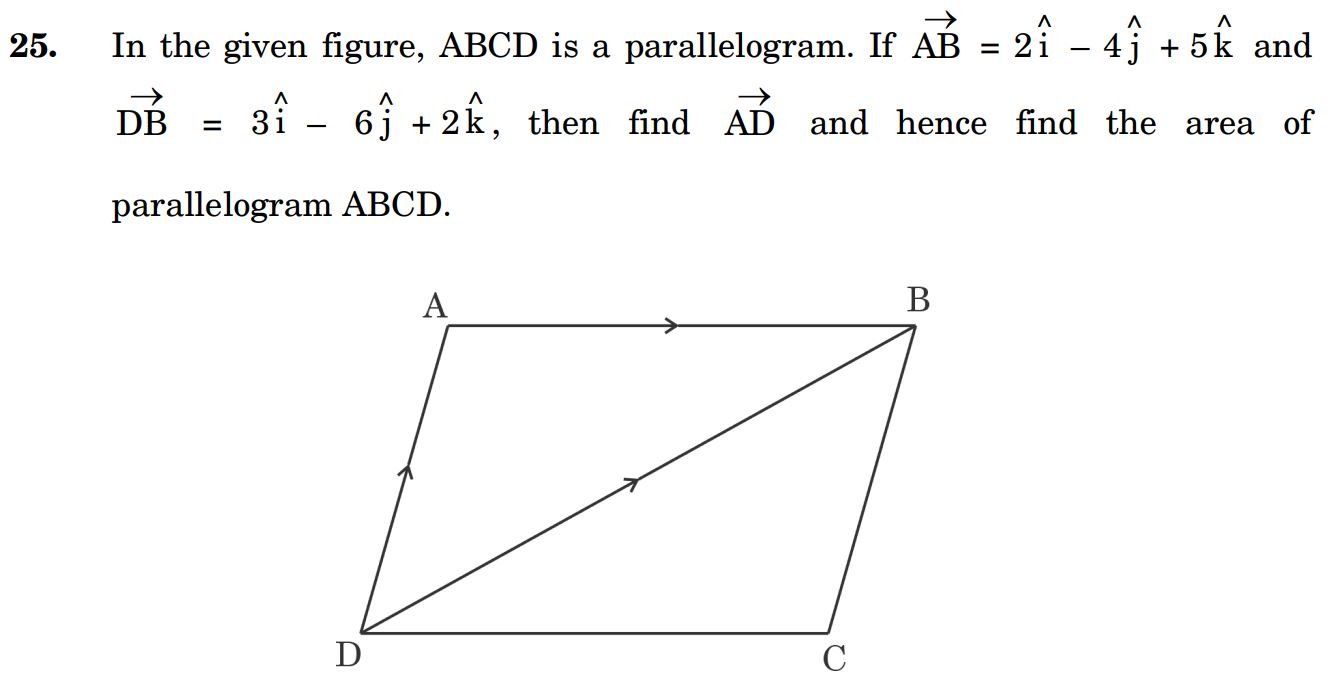
Ans.
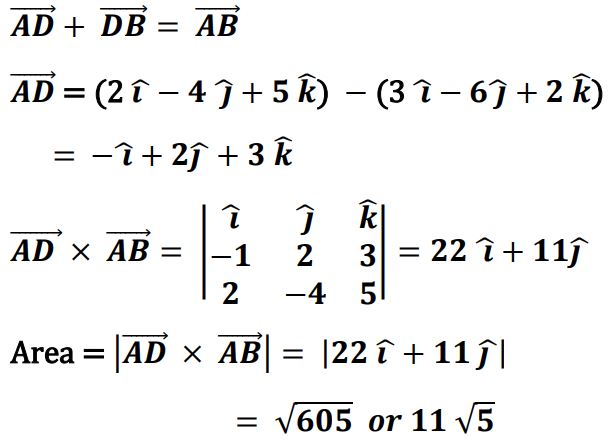
26. (a) A relation R on set A = {1, 2, 3, 4, 5} is defined as R = {(x, y) : |x2 – y2| < 8}. Check whether the relation R is reflexive, symmetric and transitive.
Ans. (a) Reflexive:
∵ |𝒙2 − 𝒙2| < 𝟖 ∀ 𝒙 ∈ 𝑨 ⇒ (𝒙, 𝒙) ∈ 𝑹 ∴ 𝑹 is reflexive.
(b) Symmetric:
Let (x,y) ∈ 𝑹 for some x,y ∈ A
∴ |𝒙2 − 𝒚2| < 𝟖 ⇒ |𝒚2 − 𝒙2| < 𝟖 ⇒ (𝒚, 𝒙) ∈ 𝑹
Hence R is symmetric.
(c) Transitive:
(1,2) , (2,3) ∈ 𝑹 as |𝟏2 − 𝟐2| < 𝟖 , |𝟐2 − 𝟑2| < 𝟖 respectively
But |𝟏2 − 𝟑2| ≮ 𝟖 ⇒ (𝟏, 𝟑) ∉ 𝑹
Hence 𝑹 is not transitive
OR
(b) A function f is defined from R → R as f(x) = ax + b, such that f(1) = 1 and f(2) = 3. Find function f(x). Hence, check whether function f(x) is one-one and onto or not.
Ans. f(x) = ax + b
Solving a + b = 1 and 2a + b = 3 to get a = 2 , b = −1
f(x) = 2x – 1
Let f (x𝟏) = f (x2) for some x𝟏, x2 ∈ 𝑹
2 x𝟏 − 𝟏 = 2 x2 − 𝟏 ⇒ x𝟏 = x2
Hence f is one – one.
Let y = 2x -1, y ∈ 𝑹 (Codomain)
⇒ x = 𝒚+1/2 ∈ 𝑹 (domain)
Also, f(x) = f(𝒚+1/2) = y
∴ f is onto.
27.
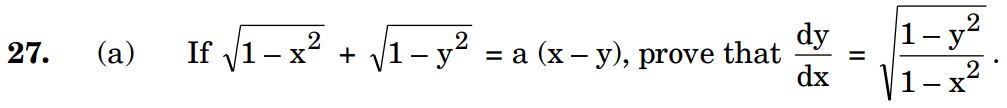
Ans.
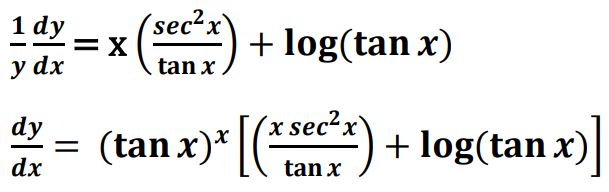
OR
(b) If y = (tan x)x, then find dy/dx.
Ans. y = (tan x)x
log y = x log (tan x)
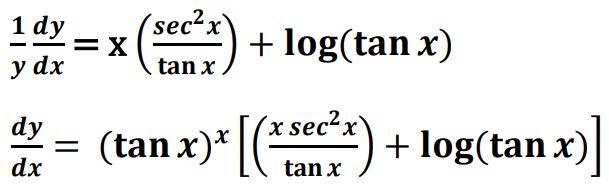
28. (a) Find :
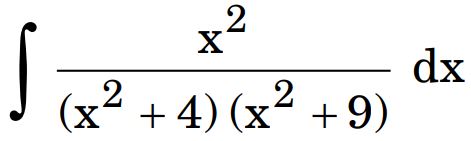
Ans.
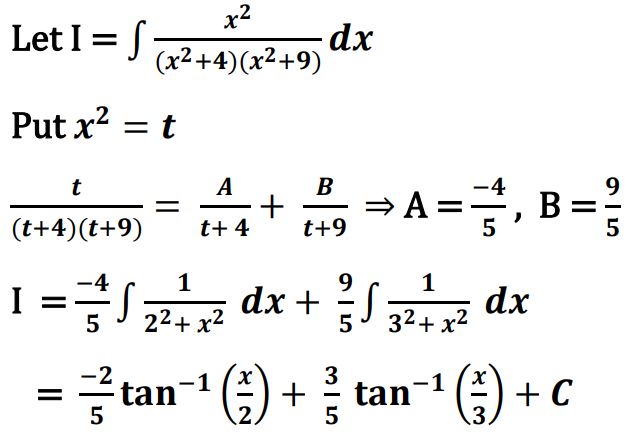
OR
(b) Evaluate :
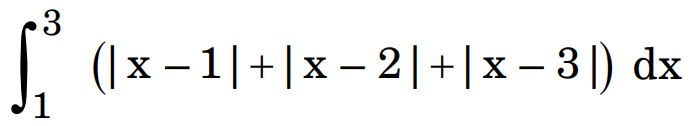
Ans.
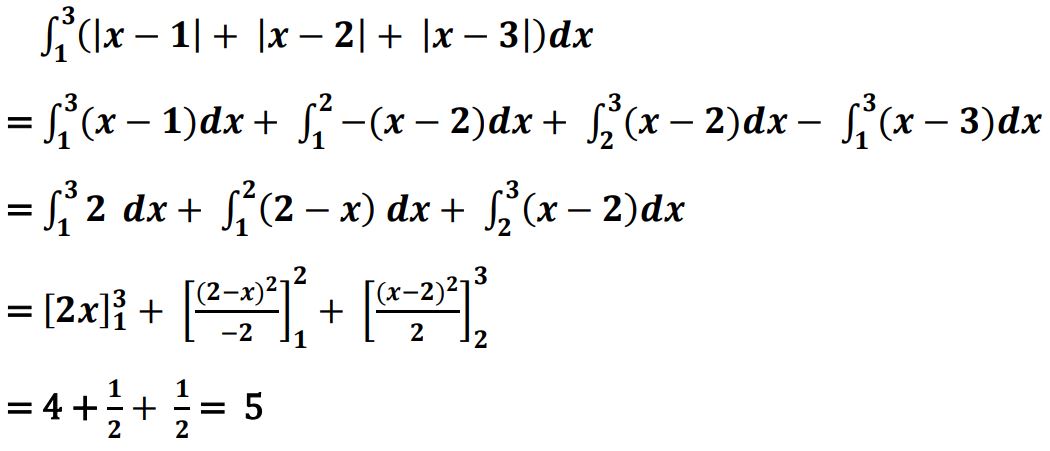
29. Find the particular solution of the differential equation given by x2 dy/dx – xy = x2 cos2 (y/2x) , given that when x = 1, y = Π/2.
Ans.
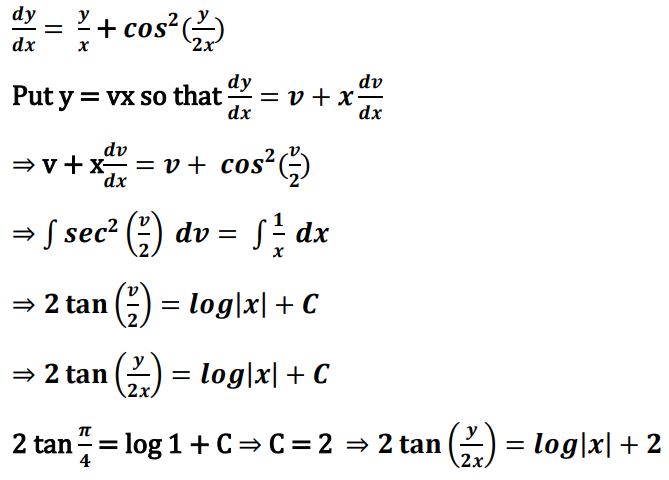
30. Solve the following linear programming problem graphically :
Maximise z = 500x + 300y,
subject to constraints
x + 2y ≤ 12
2x + y ≤ 12
4x + 5y ≥ 20
x ≥ 0, y ≥ 0
Ans. Max z = 500x + 300y
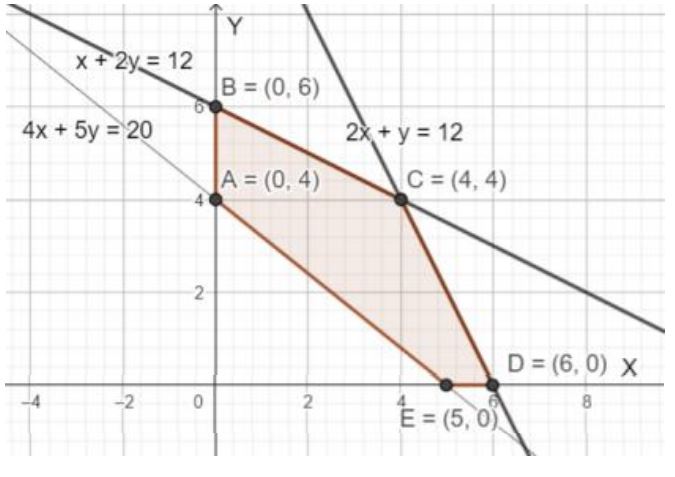
| Corner Point | Z |
| A (0,4) | 1200 |
| B (0,6) | 1800 |
| C (4,4) | 3200 |
| D (6,0) | 3000 |
| E (5,0) | 2500 |
Max z = 3200 at x = 4, y = 4
31.

Ans.
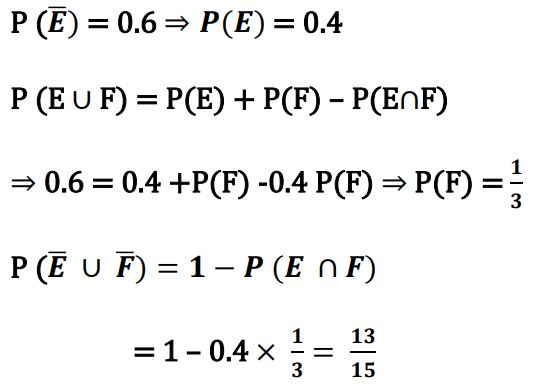
32.
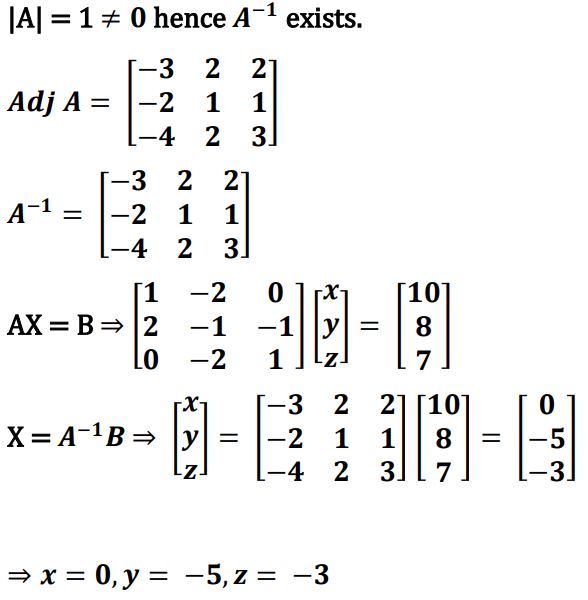
Ans.
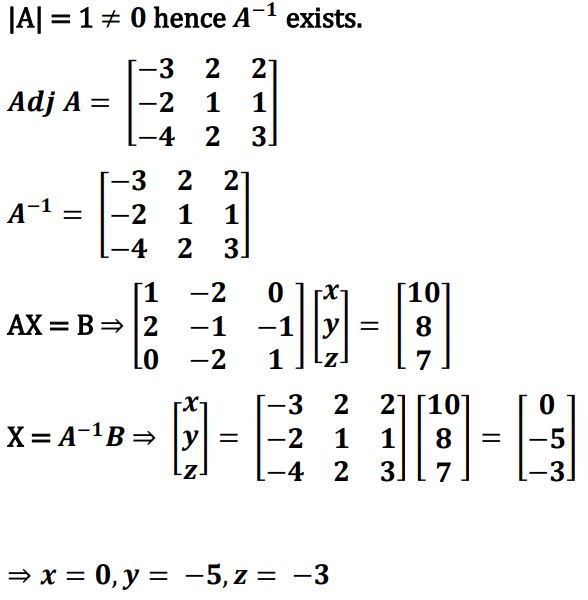
OR
33. (a) Evaluate :
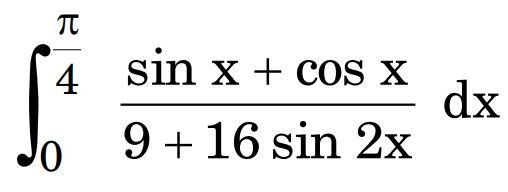
Ans.
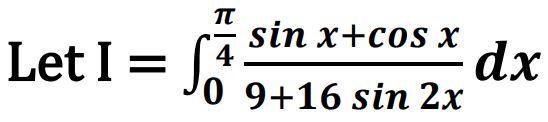
OR
(b) Evaluate :
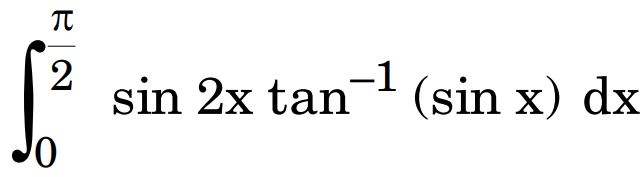
Ans.
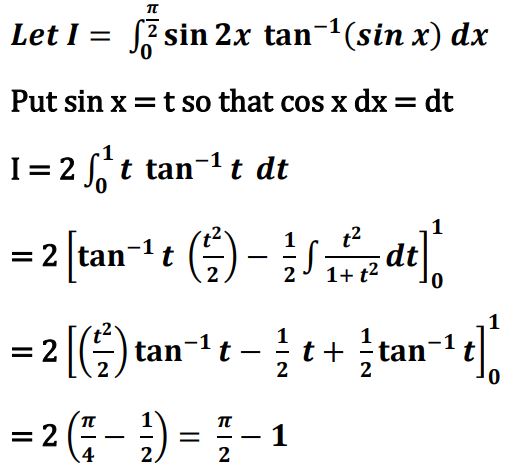
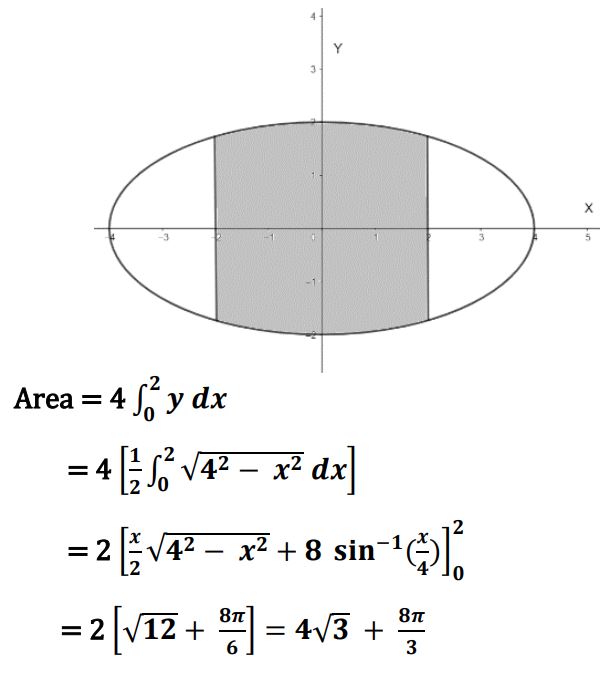
34. Using integration, find the area of the ellipse x2/16 + y2/4 = 1, included between the lines x = – 2 and x = 2.
Ans.
35. The image of point P(x, y, z) with respect to line x/1 = y – 1/2 = z – 2/3 is P' (1, 0, 7). Find the coordinates of point P.
Ans. Let foot of the perpendicular on the given line from point P be M (𝝀, 𝟐𝝀 + 𝟏, 𝟑𝝀 + 𝟐)
D. ratios of P𝑷′ are 𝝀 − 𝟏, 𝟐𝝀 + 𝟏, 𝟑𝝀 − 𝟓
1(𝝀 -1) + 2 (2𝝀 + 𝟏) + 3 (3𝝀 -5) = 0
⇒ 𝝀 = 𝟏
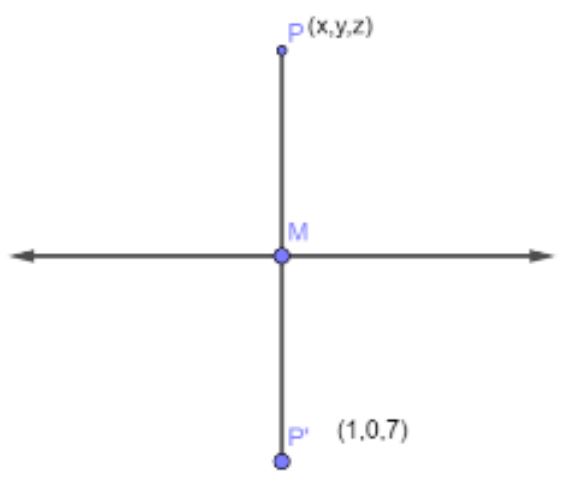
Coordinates of M(1,3,5)
𝒙+1/2 = 𝟏, 𝒚+0/2 = 𝟑, 𝒛+7/2 = 5
⇒ 𝒙 = 𝟏, 𝒚 = 𝟔, 𝒛 = 𝟑 ⇒ 𝑷(𝟏, 𝟔, 𝟑)
Case Study – 1
36. The traffic police has installed Over Speed Violation Detection (OSVD) system at various locations in a city. These cameras can capture a
speeding vehicle from a distance of 300 m and even function in the dark.
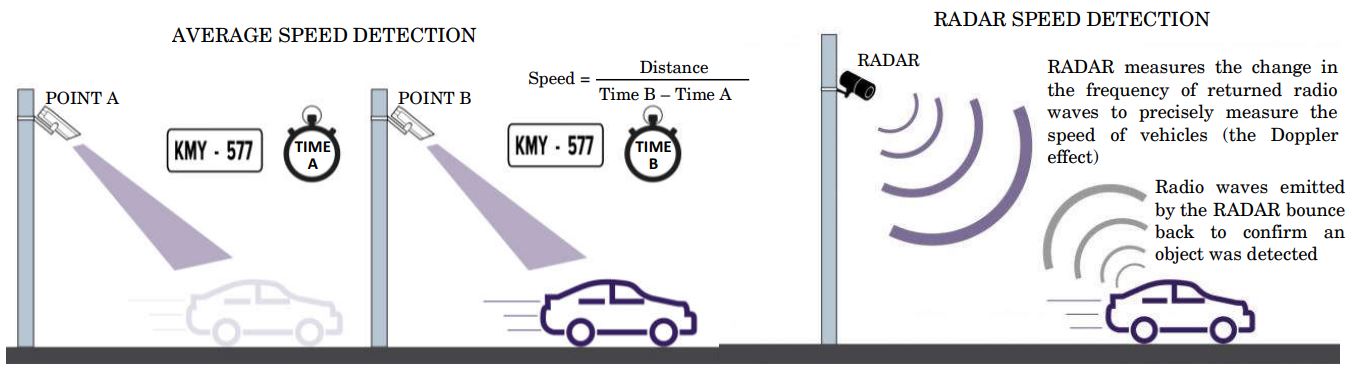
A camera is installed on a pole at the height of 5 m. It detects a car travelling away from the pole at the speed of 20 m/s. At any point, x m away from the base of the pole, the angle of elevation of the speed camera from the car C is θ.
On the basis of the above information, answer the following questions :
(i) Express θ in terms of height of the camera installed on the pole and x.
(ii) Find dθ/dx.
(iii) (a) Find the rate of change of angle of elevation with respect to time at an instant when the car is 50 m away from the pole.
Ans.
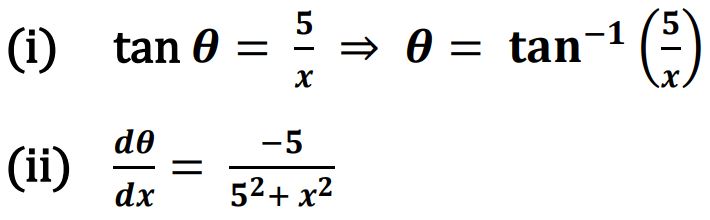
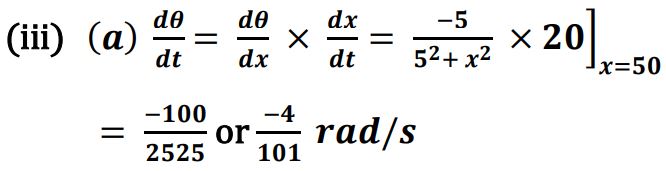
OR
(iii) (b) If the rate of change of angle of elevation with respect to time of another car at a distance of 50 m from the base of the pole is 3/101 rad/s, then find the speed of the car.
Ans.
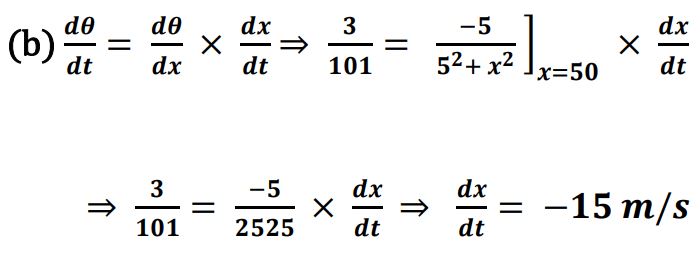
Hence the speed is 15 m/s
37. According to recent research, air turbulence has increased in various regions around the world due to climate change. Turbulence makes flights bumpy and often delays the flights.
Assume that, an airplane observes severe turbulence, moderate turbulence or light turbulence with equal probabilities. Further, the chance of an airplane reaching late to the destination are 55%, 37% and 17% due to severe, moderate and light turbulence respectively.

On the basis of the above information, answer the following questions :
(i) Find the probability that an airplane reached its destination late.
Ans. Let A denote the event of airplane reaching its destination late
E𝟏= severe turbulence
E𝟐 = moderate turbulence
E𝟑 = light turbulence
P(A) = P (E𝟏) 𝑷( 𝑨|E𝟏) + 𝑷(E𝟐)𝑷(𝑨|E𝟐) + 𝑷(E𝟑)𝑷(𝑨|E𝟑)
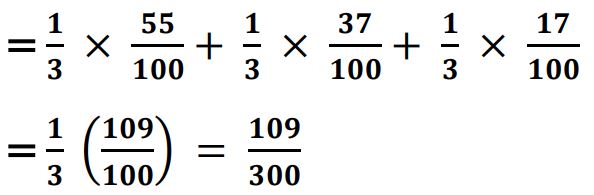
(ii) If the airplane reached its destination late, find the probability that it was due to moderate turbulence.
Ans. P (𝑬𝟐|𝑨) = 𝑷(𝑬𝟐)𝑷(𝑨|𝑬𝟐)/𝑷(𝑨)
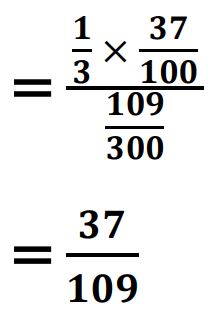
38. If a function f : X → Y defined as f(x) = y is one-one and onto, then we can define a unique function g : Y → X such that g(y) = x, where x ∈ X and y = f(x), y ∈ Y. Function g is called the inverse of function f.
The domain of sine function is R and function sine : R → R is neither one-one nor onto. The following graph shows the sine function.
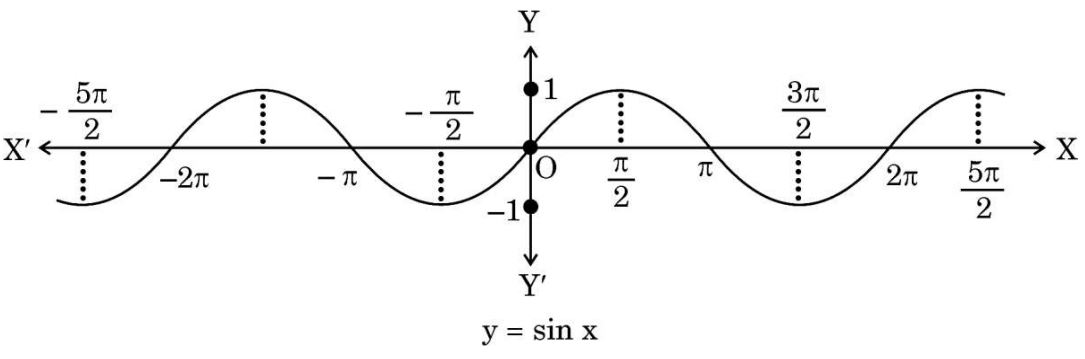
Let sine function be defined from set A to [– 1, 1] such that inverse of sine function exists, i.e., sin–1 x is defined from [– 1, 1] to A.
On the basis of the above information, answer the following questions :
(i) If A is the interval other than principal value branch, give an example of one such interval.
(ii) If sin–1 (x) is defined from [– 1, 1] to its principal value branch, find the value of sin–1 (-1/2) – sin–1 (1).
(iii) (a) Draw the graph of sin–1 x from [– 1, 1] to its principal value branch.
Ans.

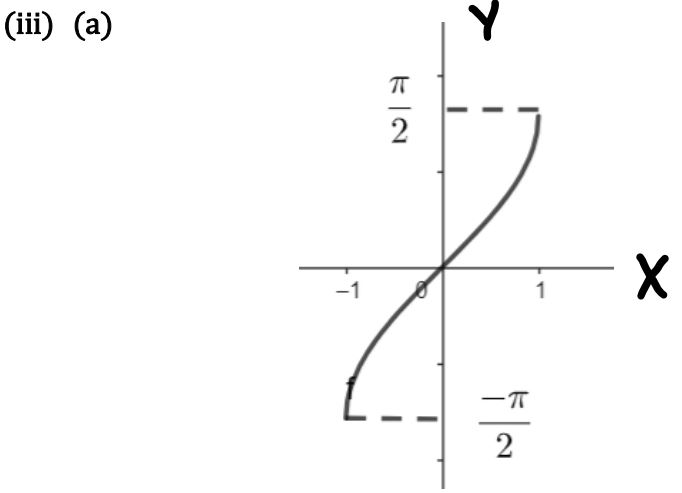
OR
(iii) (b) Find the domain and range of f(x) = 2 sin–1 (1 – x).
Ans.
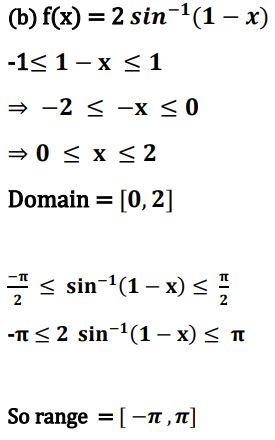
-
👉 Read Also - CBSE Class 12 Half-Yearly/Mid Term 2024-25 : Most Important Questions with Answers; PDF Download (All Subjects)
👉 Read Also - How CBSE’s New Exam Pattern Will Impact Class 11 and 12 Students
👉 CBSE Class 12 Study Materials
| CBSE Class 12 Syllabus 2024-25 | CBSE Class 12 Previous Year Papers |
| NCERT Books For Class 12 Books | NCERT Class 12 Solutions |
| CBSE Class 12 Full Study Material | CBSE Class 12 Sample Paper 2024-25 |







 Profile
Profile Signout
Signout








 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










