Physics Test

Result

Physics Test - 50

Score
-
out of -
Rank
-
out of -

TIME Taken - -

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Weekly Quiz Competition

Question 1
1 / -0

A pendulum bob is suspended on a flat car that moves with velocity v_o.The flat car is stopped by a bumper

(i) What is the angle through which the pendulum swings.

(ii) If the swing angle is$\theta=60^{\circ}$ and $l=10 \mathrm{m}$what was the initial speed of the flat car?

A
$2 \sin ^{-1}\left(\frac{v_{0}}{3 \sqrt{\mathrm{g}^{\prime}}}\right) 5 \mathrm{m} / \mathrm{s}$

B
$2 \sin ^{-1}\left(\frac{v_{0}}{2 \sqrt{\mathrm{g}} t}\right) 10 \mathrm{m} / \mathrm{s}$

C
$3 \sin ^{-1}\left(\frac{v_{0}}{4 \sqrt{\mathrm{g}^{l}}}\right) 15 \mathrm{m} / \mathrm{s}$

D
$4 \sin ^{-1}\left(\frac{v_{0}}{2 \sqrt{g l}}\right) 20 \mathrm{m} / \mathrm{s}$

Solution

By definition of bulk modulus,

$\begin{aligned} \mathrm{B}_{\mathrm{W}} &=-\mathrm{V} \frac{\Delta \mathrm{p}}{\Delta \mathrm{v}}=-100 \times \frac{\left(100 \times 1.013 \times 10^{5}\right)}{(99.5-100)} \\ &=2.026 \times 10^{9} \mathrm{N} / \mathrm{m}^{2} \end{aligned}$

Now as isothermal elasticity of a gas is equal to its pressure,

$\mathrm{B}_{\mathrm{A}}=\mathrm{E}_{\theta}=\mathrm{p}_{0}=1.013 \times 10^{5} \mathrm{N} / \mathrm{m}^{2}$

So that $\frac{B u}{B_{A}}=\frac{C_{A}}{C_{W}}=\frac{2.026 \times 10^{9}}{1.013 \times 10^{5}}=2 \times 10^{4} \quad\left[\right.$ as $\left.C=\frac{1}{B}\right]$

i.e., bulk modulus of water is very large as compared to air. This means that air is about 20,000 times more compressive than water, i.e., the average distance between air molecules is much larger than between water molecules.

Hence, the correct option is (B)
Question 2
1 / -0

A balloon is moving upwards with a speed of 20 m/s. When it is at a height of 14 m from ground in front of a plane mirror in as shown in figure, a boy drops himself from the balloon. Find the time duration for which he will see the image of source S placed symmetrically before plane mirror during free fall.

A
1.7 s

B
1.9 s

C
2.6 s

D
2.1 s

Solution

$\begin{aligned} \frac{\mathrm{PQ}}{\mathrm{BP}} &=\frac{\mathrm{IH}}{\mathrm{BH}}=\frac{\mathrm{HS}}{\mathrm{BH}} \\ \therefore \quad \mathrm{FQ} &=(\mathrm{BF})\left(\frac{\mathrm{HS}}{\mathrm{BH}}\right) \\=&(5)\left(\frac{1.0}{0.5}\right) \\=& 10 \mathrm{m} \\ \mathrm{FC} &=2+10=12 \mathrm{m} \end{aligned}$

The boy has dropped himself at point $F$. So, his velocity is $20 \mathrm{m} / \mathrm{s}$ in upward direction. Let us first find the time to move from $F$ to topmost point and then from topmost point to point $C$. From

\[
\begin{aligned}
\mathrm{s} &=\mathrm{ut}+\frac{1}{2} \mathrm{at}^{2} \text { we have } \\
-12 &=(20 t)+\frac{1}{2}(-10) \mathrm{t}^{2}
\end{aligned}
\]
Solving this equation we get, $t_{1}=4.53 \mathrm{s}$ Velocity of boy at point $Q$.
$v=\sqrt{(20)^{2}-2 \times 10 \times 10}=14.14 \mathrm{m} / \mathrm{s} \quad\left(v^{2}=u^{2}-2 \mathrm{gh}\right)$
Time taken to move the boy from $Q$ to topmost point and then from topmost point to $Q$ will be
$t_{2}=\frac{2 v}{\mathrm{g}}=2.83 \mathrm{s}$
$\therefore$ Time required time is $: t=t_{1}-t_{2}=1.7 \mathrm{s}$
Hence, the correct option is (A)
Question 3
1 / -0

The peak emission from a body at a certain temperature occurs at a wavelength of $9000 Å .$ On increasing its temperature the total radiation emitted is increased to 81 times. At the initial temperature when the peak radiation from the black body is incident on a metal surface it does not cause any photoemission from the surface. After the increase of temperature the peak radiation from the black body causes photoemission. To bring these photoelectrons to rest, potential equivalent to the excitation energy between the n = 2 to n = 3 Bohr levels of hydrogen atom is required. Find the work function of the metal. [h = 6.62 × 10^-34 J-s and c = 3 × 10⁸ m/s]

A
2.25 eV

B
4.47 eV

C
7.72 eV

D
9.65 eV

Solution

Let $T_{1}$ be the initial tamprature and $T_{2}$ be the increased tamprature of the black body.
According to Stefan's law:
$\left(\frac{T_{2}}{T_{2}}\right)=81=(3)^{4}$
$T_{2}=3 T_{1}$
Also $\lambda_{1} T_{1}=i_{2} T_{2}$

$\lambda_{2}=\frac{\lambda_{1 \times I_{1}}}{T_{2}}=\frac{9000 \times T_{1}}{3 T_{1}}=3000$ A

Now $\frac{h v}{\lambda_{2}}-W=e V_{0}$ or $\frac{h v}{\lambda_{2}}-W=13.6\left(\frac{1}{2^{2}}-\frac{1}{3^{2}}\right)$
Solving we get $, W=2.25 \mathrm{eV}$

Hence optioon A is the correct answer.
Question 4
1 / -0

Q charge is uniformly distributed over the curve surface of a right circular cone of semi-vertical angle θ and height h. The cone is uniformly rotated about its axis at angular velocity ω. Calculated associated magnetic dipole moment.(H>R)

A
$\frac{q \omega h^{2} \tan ^{2} \theta}{4}$

B
$\frac{\tan ^{2} \theta q \omega h^{2}}{2}$

C
$\frac{\tan ^{2} \theta q \omega h^{2}}{3}$

D
$\frac{\tan ^{2} \theta q \omega h^{2}}{1}$

Solution

$A=$ Surface area of cone
$=\pi R \sqrt{R^{2}+h^{2}}$
$d A=2 \pi y d x$

$\tan \theta=\frac{y}{x}$
$y=x \tan \theta$
$d q=\frac{q}{A} d A$
$d i=d q \frac{\omega}{2 \pi}$
$=\frac{q}{\pi R \sqrt{R^{2}+h^{2}}} \frac{\omega}{2 \pi} \times 2 \pi y d x$
$d m=d i A$
$=\frac{q \omega}{\pi R \sqrt{R^{2}+h^{2}}} x \tan \theta d x \times \pi y^{2}$
$=\frac{q \omega}{\pi R \sqrt{R^{2}+h^{2}}} x \tan \theta d x \times \pi \times x^{2} \tan ^{2} \theta$
$\int d m=\frac{q \omega}{R \sqrt{R^{2}+h^{2}}} \int_{x=0}^{x=h} x^{3} \tan ^{3} \theta d x$
$=\frac{q \omega}{R \sqrt{R^{2}+h^{2}}} \times \frac{h^{4}}{4} \tan ^{3} \theta$
$=\frac{q \omega h^{4} \tan ^{4} \theta}{4 R \sqrt{R^{2}+h^{2}}}$
$=\frac{q \omega h^{4} \tan ^{3} \theta}{4 R h}(\because h>>R)$
$=\frac{q \omega h^{2} \tan ^{2} \theta}{4}$
key concept
Magnetic dipole and dipole moment
Magnetic Dipole Moment
From the expression for the torque on a current loop, the characteristics of the current loop are summarized in its magnetic moment

If there are $\mathrm{N}$ loops, then $\mu=\mathrm{NIA}$
The magnetic moment can be considered to be a vector quantity with direction perpendicular to the current loop in the right-hand-rule direction.
Hence, the correct option is (A)
Question 5
1 / -0

A beam of ultraviolet radiation having wavelength between 100 nm and 200 nm is incident on a sample of atomic hydrogen gas. Assuming that the atoms are in ground state, which wavelengths will have low intensity in the transmitted beam ?

A
104 nm

B
103 nm

C
105 nm

D
100 nm

Solution

The energy of a photon corresponding to $\lambda=100 \mathrm{nm}$ is
\frac{1242 \mathrm{eV} \mathrm{nm}}{100 \mathrm{nm}}=12 \cdot 42 \mathrm{eV}
and the corresponding to $\lambda=200 \mathrm{nm}$ is $6.21 \mathrm{eV}$. The energy needed to take the atom from the ground state to the first excited state is
\mathrm{E}_{2}-\mathrm{E}_{1}=13.6 \mathrm{eV}-3.4 \mathrm{eV}=10.2 \mathrm{eV}
to the second excited state is
\mathrm{E}_{3}-\mathrm{E}_{1}=13.6 \mathrm{eV}-1.5 \mathrm{eV}=12.1 \mathrm{eV}
to the third excited state is
\mathrm{E}_{4}-\mathrm{E}_{1}=13.6 \mathrm{eV}-0.85 \mathrm{eV}=12.75 \mathrm{eV}, \text { etc. }
Thus, $10.2 \mathrm{eV}$ photons and $12.1 \mathrm{eV}$ photons have large probability of being absorbed from the given range $6.21 \mathrm{eV}$ to $12.42 \mathrm{eV} .$ The corresponding wavelengths are
and
\begin{array}{c}
\lambda_{1}=\frac{1242 \mathrm{eV} \mathrm{nm}}{10 \cdot 2 \mathrm{eV}}=122 \mathrm{nm} \\
\lambda_{2}=\frac{1242 \mathrm{eV}}{12 \cdot 1 \mathrm{eV}}=103 \mathrm{nm}
\end{array}
These wavelengths will have low intensity in the transmitted beam.
Concepts:
Main Concept:
Bohr's PostulatesBohr Model:
Niels Bohr applied classical mechanics, electromagnetism and Planck's quantum theory to modify the Rutherford's model and proposed his atomic model in 1913 . His model gives satisfactory explanation of stable atomic structure and emission of line spectra by hydrogen atom. He presented his theory in the form of 3 postulates:
Postulate 1: The electron in a hydrogen atom revolves in circular orbit around the nucleus with nucleus at the centre of orbit. The necessary centripetal force for circular motion is provided by electrostatic force of attraction between the positively charged nucleus and negatively charged electron.
Hydrogen atom consists of only one electron and the nucleus. Let an electron of mass $\mathrm{m}$ revolves with speed $\mathrm{v}$ in an orbit of radius r. the charge on nucleus must be te to make atom electrically neutral.

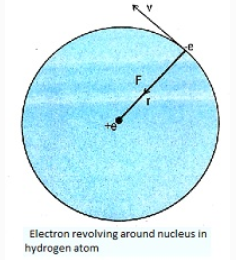
The force of attraction between electron and nucleus is given by Coulomb's law:
Postulate 2 :
The electron revolves around the nucleus only in those orbits for which the angular momentum is equal to an integral multiple of $\mathrm{h} / 2 \pi,$ where $\mathrm{h}$ is Planck's constant. These orbits are called stable or stationary (or permitted or quantized or Bohr orbits) and electron does not radiate energy whole revolving in these orbits i.e. its energy remains constant and hence stability of atomic structure. The force of attraction between electron and nucleus is given by Coulomb's law:
$\mathrm{F}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\rho^{2}}{\mathrm{r}^{2}}$
The centripetal force is given by $\frac{\mathrm{mv}^{2}}{\mathrm{r}}$
$\therefore$ Centripetal force $=$ Electrostatic force of attraction.
$\frac{\mathrm{mv}^{2}}{\mathrm{r}}=\frac{1}{\pi \varepsilon_{0}} \frac{\mathrm{e}^{2}}{\mathrm{r}^{2}}$
That is electrons revolve in only those orbits that satisfies the equation. The integer 'n' is called principal quantum number. It also designates the orbit number.
Hence, the correct option is (B)
Question 6
1 / -0

A large tank filled with water to a height 'h' is to be emptied through a small hole at the bottom. The ratio of times taken for the level of water to fall from $\mathrm{h}$ to $\frac{\mathrm{h}}{2}$ and from $\frac{\mathrm{h}}{2}$ to zero is :

A
$\sqrt{2}$

B
$\frac{1}{\sqrt{2}}$

C
$\sqrt{2} - 1$

D
$\frac{1}{\sqrt{2} - 1}$

Solution

Time taken for the level to fall from $\mathrm{H}$ to $\mathrm{H}^{\prime}$
$\mathrm{t}=\frac{\mathrm{A}}{\mathrm{A}_{0}} \quad \sqrt{\frac{2}{\mathrm{g}}}\left[\sqrt{\mathrm{H}}-\sqrt{\mathrm{H}^{\prime}}\right]$
According to problem the time taken for the level to fall from h to $\frac{h}{2}$
$t_{1}=\frac{A}{A_{0}} \quad \sqrt{\frac{2}{g}}\left[\sqrt{h}-\sqrt{\frac{h}{2}}\right]$
and similarly time taken for the level to fall from $\frac{h}{2}$
$t_{2}=\frac{A}{A_{0}} \quad \sqrt{\frac{2}{g}}\left[\sqrt{\frac{h}{2}}-0\right]$
$\therefore \frac{t_{1}}{t_{2}}=\frac{1-\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{2}}-0}=\sqrt{2}-1$
Hence, the correct option is (C)
Question 7
1 / -0

Initially car A is 10.5 m ahead of car B. Both start moving at time t = 0 in the same direction along a straight line. The velocity time graph of two cars is shown in figure. The time when the car B will catch the car A, will be :

A
t = 21 sec

B
t=2 $\sqrt{5}$ sec

C
t = 20 sec

D
t = 1 sec

Solution

$\mathrm{x}_{\mathrm{A}}=\mathrm{x}_{\mathrm{B}}$
$10.5+10 \mathrm{t}=\frac{1}{2} \mathrm{at}^{2} \quad\left[\mathrm{a}=\tan 45^{0}\right]$
$\mathrm{t}^{2}-20 \mathrm{t}-21=0$
$\mathrm{t}=\frac{20 \pm \sqrt{400+84}}{2}$
$\mathrm{t}=21 \mathrm{sec}$
Hence, the correct option is (A)
Question 8
1 / -0

The intensity of the light coming from one of the slits in YDSE is double the intensity from the other slit. Find the ratio of maximum intensity to minimum intensity in the interference fringe pattern observed.

A
32

B
36

C
38

D
34

Solution

When the flat car collides with the bumper, due to inertia of motion the bob swings forward No work is done by tension of string on the bob therefore energy is conserved

$\mathrm{KE}_{\mathrm{A}}+\mathrm{PE}_{\mathrm{A}}=\mathrm{KE}_{\mathrm{B}}+\mathrm{PE}_{\mathrm{B}}$

$v_{0}^{2}=2 \mathrm{g} l(1-\cos \theta)$

$v_{0}^{2}=4 \mathrm{g} l \sin ^{2} \theta / 2$

$\therefore \theta=2 \sin ^{-1}\left(\frac{w_{0}}{2 \sqrt{g l}}\right)$

For,

$\theta=60^{\circ}, l=10 \mathrm{m}, \mathrm{g}=10 \mathrm{m} / \mathrm{s}^{2}$

$v_{0}^{2}=4 \times 10 \times 10 \sin ^{2}(30)=100$

$v_{0}=10 \mathrm{m} / \mathrm{s}$
Hence, the correct option is (D)
Question 9
1 / -0

A truck starts from origin, accelerating with 'a' m/sec² in positive x - axis direction. After 2 seconds a man standing at the starting point of the truck projected a ball at an angle 30⁰ with velocity 'v' m/s. Find the relation between 'a' and 'v' such that ball hits the truck. (assume truck is moving on horizontal plane and man projected the ball from the same horizontal level of truck).

A

$\nu=2 \mathrm{g}\left[\frac{\sqrt{\frac{\mathrm{a}}{\mathrm{B} \sqrt{3}}}}{1-\sqrt{\frac{\mathrm{s}}{\mathrm{g} \sqrt{3}}}}\right]$

B

$\nu=2 \mathrm{g}\left[\frac{\sqrt{\frac{\mathrm{a}}{\mathrm{g}}}}{1-\sqrt{\frac{\mathrm{a}}{\mathrm{g}}}}\right]$

C

$\nu=g\left[\frac{\sqrt{\frac{a}{g \sqrt{3}}}}{1-\sqrt{\frac{a}{g \sqrt{3}}}}\right]$

D
$\nu=g\left[\frac{\sqrt{\frac{a}{8}}}{1-\sqrt{\frac{a}{g}}}\right]$

Solution

$\nu \sin 30^{\circ}(t-2)-\frac{1}{2} g(t-2)^{2}=0$
$\nu \cos 30^{\circ}(t-2)=\frac{1}{2} a t^{2}$
$\tan 30^{\circ}=\frac{\mathrm{g}(\mathrm{t}-2)^{2}}{\mathrm{at}^{2}} \Rightarrow \frac{\mathrm{t}-2}{\mathrm{t}}=\sqrt{\frac{\mathrm{a}}{\mathrm{g} \sqrt{3}}}$
$\Rightarrow t\left(1-\sqrt{\frac{a}{g \sqrt{3}}}\right)=2$
$\Rightarrow t=\frac{2}{1-\sqrt{\frac{3}{8 \sqrt{3}}}}$
$\Rightarrow \nu=\frac{g(t-2)}{2 \sin 30^{\circ}}$
$\Rightarrow g\left[\frac{2}{1-\sqrt{\frac{2}{8 \sqrt{3}}}}-2\right]$
$\nu=2 \mathrm{g}\left[\frac{\sqrt{\frac{0}{8 \sqrt{3}}}}{1-\sqrt{\frac{2}{8 \sqrt{3}}}}\right]$
Hence, the correct option is (A)
Question 10
1 / -0

A battery is supplying power to a tape-recorder by cable of resistance of 0.2 $Ω$ . If the battery is generating 50 W power at 5V, then power received by tape-recorder is :

A
50 W

B
45 W

C
30 W

D
48 W

Solution

P = VI, $50 = 5 \times I$
$I = 10 A$

Power lost in cable= I²R = 10 × 10 × 0·2 = 2W

Power supplied to T.R= 50 W - 2W = 48W

Concepts :
Main Concept :
Electric PowerThe rate at which electrical energy is dissipated into other forms of energy is called electrical power i.e.
$P=\frac{W}{t}=V \cdot i=i^{2} R=\frac{V^{2}}{R}$
Units: It's S.I. unit is Joule/sec or Watt
Bigger S.I. units are KW, MW and HP, remember 1 HP = 746 Watt
Hence, the correct option is (D)