Reading Comprehension Test - 2

After reading the passage choose the best answer to the given question based on what is stated or implied in the passage and in any accompanying graphics (such as a table or graph).

Nearly a half-century ago, Peter Higgs and a handful of other physicists were trying to understand the origin of a basic physical feature: mass. You can think of mass as an object’s heft or, a little more 5 precisely, as the resistance it offers to having its motion changed. Push on a freight train (or a feather) to increase its speed, and the resistance you feel reflects its mass. At a microscopic level, the freight train’s mass comes from its constituent 10 molecules and atoms, which are themselves built from fundamental particles, electrons and quarks. But where do the masses of these and other fundamental particles come from? When physicists in the 1960s modeled the 15 behavior of these particles using equations rooted in quantum physics, they encountered a puzzle. If they imagined that the particles were all massless, then each term in the equations clicked into a perfectly symmetric pattern, like the tips of a perfect 20 snowflake. And this symmetry was not just mathematically elegant. It explained patterns evident in the experimental data. But—and here’s the puzzle—physicists knew that the particles did have mass, and when they modified the equations to 25 account for this fact, the mathematical harmony was spoiled. The equations became complex and unwieldy and, worse still, inconsistent. What to do? Here’s the idea put forward by Higgs. Don’t shove the particles’ masses down the throat of 30 the beautiful equations. Instead, keep the equations pristine and symmetric, but consider them operating within a peculiar environment. Imagine that all of space is uniformly filled with an invisible substance—now called the Higgs field—that exerts a 35 drag force on particles when they accelerate through it. Push on a fundamental particle in an effort to increase its speed and, according to Higgs, you would feel this drag force as a resistance. Justifiably, you would interpret the resistance as the particle’s mass. 40 For a mental toehold, think of a ping-pong ball submerged in water. When you push on the ping-pong ball, it will feel much more massive than it does outside of water. Its interaction with the watery environment has the effect of endowing it with mass. 45 So with particles submerged in the Higgs field. In 1964, Higgs submitted a paper to a prominent physics journal in which he formulated this idea mathematically. The paper was rejected. Not because it contained a technical error, but because the 50 premise of an invisible something permeating space, interacting with particles to provide their mass, well, it all just seemed like heaps of overwrought speculation. The editors of the journal deemed it “of no obvious relevance to physics.” 55 But Higgs persevered (and his revised paper appeared later that year in another journal), and physicists who took the time to study the proposal gradually realized that his idea was a stroke of genius, one that allowed them to have their cake and eat it 60 too. In Higgs’s scheme, the fundamental equations can retain their pristine form because the dirty work of providing the particles’ masses is relegated to the environment. While I wasn’t around to witness the initial 65 rejection of Higgs’s proposal in 1964 (well, I was around, but only barely), I can attest that by the mid-1980s, the assessment had changed. The physics community had, for the most part, fully bought into the idea that there was a Higgs field permeating 70 space. In fact, in a graduate course I took that covered what’s known as the Standard Model of Particle Physics (the quantum equations physicists have assembled to describe the particles of matter and the dominant forces by which they influence 75 each other), the professor presented the Higgs field with such certainty that for a long while I had no idea it had yet to be established experimentally. On occasion, that happens in physics. Mathematical equations can sometimes tell such a convincing tale, 80 they can seemingly radiate reality so strongly, that they become entrenched in the vernacular of working physicists, even before there’s data to confirm them.

After reading the passage choose the best answer to the given question based on what is stated or implied in the passage and in any accompanying graphics (such as a table or graph).

Nearly a half-century ago, Peter Higgs and a handful of other physicists were trying to understand the origin of a basic physical feature: mass. You can think of mass as an object’s heft or, a little more 5 precisely, as the resistance it offers to having its motion changed. Push on a freight train (or a feather) to increase its speed, and the resistance you feel reflects its mass. At a microscopic level, the freight train’s mass comes from its constituent 10 molecules and atoms, which are themselves built from fundamental particles, electrons and quarks. But where do the masses of these and other fundamental particles come from? When physicists in the 1960s modeled the 15 behavior of these particles using equations rooted in quantum physics, they encountered a puzzle. If they imagined that the particles were all massless, then each term in the equations clicked into a perfectly symmetric pattern, like the tips of a perfect 20 snowflake. And this symmetry was not just mathematically elegant. It explained patterns evident in the experimental data. But—and here’s the puzzle—physicists knew that the particles did have mass, and when they modified the equations to 25 account for this fact, the mathematical harmony was spoiled. The equations became complex and unwieldy and, worse still, inconsistent. What to do? Here’s the idea put forward by Higgs. Don’t shove the particles’ masses down the throat of 30 the beautiful equations. Instead, keep the equations pristine and symmetric, but consider them operating within a peculiar environment. Imagine that all of space is uniformly filled with an invisible substance—now called the Higgs field—that exerts a 35 drag force on particles when they accelerate through it. Push on a fundamental particle in an effort to increase its speed and, according to Higgs, you would feel this drag force as a resistance. Justifiably, you would interpret the resistance as the particle’s mass. 40 For a mental toehold, think of a ping-pong ball submerged in water. When you push on the ping-pong ball, it will feel much more massive than it does outside of water. Its interaction with the watery environment has the effect of endowing it with mass. 45 So with particles submerged in the Higgs field. In 1964, Higgs submitted a paper to a prominent physics journal in which he formulated this idea mathematically. The paper was rejected. Not because it contained a technical error, but because the 50 premise of an invisible something permeating space, interacting with particles to provide their mass, well, it all just seemed like heaps of overwrought speculation. The editors of the journal deemed it “of no obvious relevance to physics.” 55 But Higgs persevered (and his revised paper appeared later that year in another journal), and physicists who took the time to study the proposal gradually realized that his idea was a stroke of genius, one that allowed them to have their cake and eat it 60 too. In Higgs’s scheme, the fundamental equations can retain their pristine form because the dirty work of providing the particles’ masses is relegated to the environment. While I wasn’t around to witness the initial 65 rejection of Higgs’s proposal in 1964 (well, I was around, but only barely), I can attest that by the mid-1980s, the assessment had changed. The physics community had, for the most part, fully bought into the idea that there was a Higgs field permeating 70 space. In fact, in a graduate course I took that covered what’s known as the Standard Model of Particle Physics (the quantum equations physicists have assembled to describe the particles of matter and the dominant forces by which they influence 75 each other), the professor presented the Higgs field with such certainty that for a long while I had no idea it had yet to be established experimentally. On occasion, that happens in physics. Mathematical equations can sometimes tell such a convincing tale, 80 they can seemingly radiate reality so strongly, that they become entrenched in the vernacular of working physicists, even before there’s data to confirm them.

After reading the passage choose the best answer to the given question based on what is stated or implied in the passage and in any accompanying graphics (such as a table or graph).

Nearly a half-century ago, Peter Higgs and a handful of other physicists were trying to understand the origin of a basic physical feature: mass. You can think of mass as an object’s heft or, a little more 5 precisely, as the resistance it offers to having its motion changed. Push on a freight train (or a feather) to increase its speed, and the resistance you feel reflects its mass. At a microscopic level, the freight train’s mass comes from its constituent 10 molecules and atoms, which are themselves built from fundamental particles, electrons and quarks. But where do the masses of these and other fundamental particles come from? When physicists in the 1960s modeled the 15 behavior of these particles using equations rooted in quantum physics, they encountered a puzzle. If they imagined that the particles were all massless, then each term in the equations clicked into a perfectly symmetric pattern, like the tips of a perfect 20 snowflake. And this symmetry was not just mathematically elegant. It explained patterns evident in the experimental data. But—and here’s the puzzle—physicists knew that the particles did have mass, and when they modified the equations to 25 account for this fact, the mathematical harmony was spoiled. The equations became complex and unwieldy and, worse still, inconsistent. What to do? Here’s the idea put forward by Higgs. Don’t shove the particles’ masses down the throat of 30 the beautiful equations. Instead, keep the equations pristine and symmetric, but consider them operating within a peculiar environment. Imagine that all of space is uniformly filled with an invisible substance—now called the Higgs field—that exerts a 35 drag force on particles when they accelerate through it. Push on a fundamental particle in an effort to increase its speed and, according to Higgs, you would feel this drag force as a resistance. Justifiably, you would interpret the resistance as the particle’s mass. 40 For a mental toehold, think of a ping-pong ball submerged in water. When you push on the ping-pong ball, it will feel much more massive than it does outside of water. Its interaction with the watery environment has the effect of endowing it with mass. 45 So with particles submerged in the Higgs field. In 1964, Higgs submitted a paper to a prominent physics journal in which he formulated this idea mathematically. The paper was rejected. Not because it contained a technical error, but because the 50 premise of an invisible something permeating space, interacting with particles to provide their mass, well, it all just seemed like heaps of overwrought speculation. The editors of the journal deemed it “of no obvious relevance to physics.” 55 But Higgs persevered (and his revised paper appeared later that year in another journal), and physicists who took the time to study the proposal gradually realized that his idea was a stroke of genius, one that allowed them to have their cake and eat it 60 too. In Higgs’s scheme, the fundamental equations can retain their pristine form because the dirty work of providing the particles’ masses is relegated to the environment. While I wasn’t around to witness the initial 65 rejection of Higgs’s proposal in 1964 (well, I was around, but only barely), I can attest that by the mid-1980s, the assessment had changed. The physics community had, for the most part, fully bought into the idea that there was a Higgs field permeating 70 space. In fact, in a graduate course I took that covered what’s known as the Standard Model of Particle Physics (the quantum equations physicists have assembled to describe the particles of matter and the dominant forces by which they influence 75 each other), the professor presented the Higgs field with such certainty that for a long while I had no idea it had yet to be established experimentally. On occasion, that happens in physics. Mathematical equations can sometimes tell such a convincing tale, 80 they can seemingly radiate reality so strongly, that they become entrenched in the vernacular of working physicists, even before there’s data to confirm them.

After reading the passage choose the best answer to the given question based on what is stated or implied in the passage and in any accompanying graphics (such as a table or graph).

Nearly a half-century ago, Peter Higgs and a handful of other physicists were trying to understand the origin of a basic physical feature: mass. You can think of mass as an object’s heft or, a little more 5 precisely, as the resistance it offers to having its motion changed. Push on a freight train (or a feather) to increase its speed, and the resistance you feel reflects its mass. At a microscopic level, the freight train’s mass comes from its constituent 10 molecules and atoms, which are themselves built from fundamental particles, electrons and quarks. But where do the masses of these and other fundamental particles come from? When physicists in the 1960s modeled the 15 behavior of these particles using equations rooted in quantum physics, they encountered a puzzle. If they imagined that the particles were all massless, then each term in the equations clicked into a perfectly symmetric pattern, like the tips of a perfect 20 snowflake. And this symmetry was not just mathematically elegant. It explained patterns evident in the experimental data. But—and here’s the puzzle—physicists knew that the particles did have mass, and when they modified the equations to 25 account for this fact, the mathematical harmony was spoiled. The equations became complex and unwieldy and, worse still, inconsistent. What to do? Here’s the idea put forward by Higgs. Don’t shove the particles’ masses down the throat of 30 the beautiful equations. Instead, keep the equations pristine and symmetric, but consider them operating within a peculiar environment. Imagine that all of space is uniformly filled with an invisible substance—now called the Higgs field—that exerts a 35 drag force on particles when they accelerate through it. Push on a fundamental particle in an effort to increase its speed and, according to Higgs, you would feel this drag force as a resistance. Justifiably, you would interpret the resistance as the particle’s mass. 40 For a mental toehold, think of a ping-pong ball submerged in water. When you push on the ping-pong ball, it will feel much more massive than it does outside of water. Its interaction with the watery environment has the effect of endowing it with mass. 45 So with particles submerged in the Higgs field. In 1964, Higgs submitted a paper to a prominent physics journal in which he formulated this idea mathematically. The paper was rejected. Not because it contained a technical error, but because the 50 premise of an invisible something permeating space, interacting with particles to provide their mass, well, it all just seemed like heaps of overwrought speculation. The editors of the journal deemed it “of no obvious relevance to physics.” 55 But Higgs persevered (and his revised paper appeared later that year in another journal), and physicists who took the time to study the proposal gradually realized that his idea was a stroke of genius, one that allowed them to have their cake and eat it 60 too. In Higgs’s scheme, the fundamental equations can retain their pristine form because the dirty work of providing the particles’ masses is relegated to the environment. While I wasn’t around to witness the initial 65 rejection of Higgs’s proposal in 1964 (well, I was around, but only barely), I can attest that by the mid-1980s, the assessment had changed. The physics community had, for the most part, fully bought into the idea that there was a Higgs field permeating 70 space. In fact, in a graduate course I took that covered what’s known as the Standard Model of Particle Physics (the quantum equations physicists have assembled to describe the particles of matter and the dominant forces by which they influence 75 each other), the professor presented the Higgs field with such certainty that for a long while I had no idea it had yet to be established experimentally. On occasion, that happens in physics. Mathematical equations can sometimes tell such a convincing tale, 80 they can seemingly radiate reality so strongly, that they become entrenched in the vernacular of working physicists, even before there’s data to confirm them.

After reading the passage choose the best answer to the given question based on what is stated or implied in the passage and in any accompanying graphics (such as a table or graph).

Nearly a half-century ago, Peter Higgs and a handful of other physicists were trying to understand the origin of a basic physical feature: mass. You can think of mass as an object’s heft or, a little more 5 precisely, as the resistance it offers to having its motion changed. Push on a freight train (or a feather) to increase its speed, and the resistance you feel reflects its mass. At a microscopic level, the freight train’s mass comes from its constituent 10 molecules and atoms, which are themselves built from fundamental particles, electrons and quarks. But where do the masses of these and other fundamental particles come from? When physicists in the 1960s modeled the 15 behavior of these particles using equations rooted in quantum physics, they encountered a puzzle. If they imagined that the particles were all massless, then each term in the equations clicked into a perfectly symmetric pattern, like the tips of a perfect 20 snowflake. And this symmetry was not just mathematically elegant. It explained patterns evident in the experimental data. But—and here’s the puzzle—physicists knew that the particles did have mass, and when they modified the equations to 25 account for this fact, the mathematical harmony was spoiled. The equations became complex and unwieldy and, worse still, inconsistent. What to do? Here’s the idea put forward by Higgs. Don’t shove the particles’ masses down the throat of 30 the beautiful equations. Instead, keep the equations pristine and symmetric, but consider them operating within a peculiar environment. Imagine that all of space is uniformly filled with an invisible substance—now called the Higgs field—that exerts a 35 drag force on particles when they accelerate through it. Push on a fundamental particle in an effort to increase its speed and, according to Higgs, you would feel this drag force as a resistance. Justifiably, you would interpret the resistance as the particle’s mass. 40 For a mental toehold, think of a ping-pong ball submerged in water. When you push on the ping-pong ball, it will feel much more massive than it does outside of water. Its interaction with the watery environment has the effect of endowing it with mass. 45 So with particles submerged in the Higgs field. In 1964, Higgs submitted a paper to a prominent physics journal in which he formulated this idea mathematically. The paper was rejected. Not because it contained a technical error, but because the 50 premise of an invisible something permeating space, interacting with particles to provide their mass, well, it all just seemed like heaps of overwrought speculation. The editors of the journal deemed it “of no obvious relevance to physics.” 55 But Higgs persevered (and his revised paper appeared later that year in another journal), and physicists who took the time to study the proposal gradually realized that his idea was a stroke of genius, one that allowed them to have their cake and eat it 60 too. In Higgs’s scheme, the fundamental equations can retain their pristine form because the dirty work of providing the particles’ masses is relegated to the environment. While I wasn’t around to witness the initial 65 rejection of Higgs’s proposal in 1964 (well, I was around, but only barely), I can attest that by the mid-1980s, the assessment had changed. The physics community had, for the most part, fully bought into the idea that there was a Higgs field permeating 70 space. In fact, in a graduate course I took that covered what’s known as the Standard Model of Particle Physics (the quantum equations physicists have assembled to describe the particles of matter and the dominant forces by which they influence 75 each other), the professor presented the Higgs field with such certainty that for a long while I had no idea it had yet to be established experimentally. On occasion, that happens in physics. Mathematical equations can sometimes tell such a convincing tale, 80 they can seemingly radiate reality so strongly, that they become entrenched in the vernacular of working physicists, even before there’s data to confirm them.

After reading the passage choose the best answer to the given question based on what is stated or implied in the passage and in any accompanying graphics (such as a table or graph).

Nearly a half-century ago, Peter Higgs and a handful of other physicists were trying to understand the origin of a basic physical feature: mass. You can think of mass as an object’s heft or, a little more 5 precisely, as the resistance it offers to having its motion changed. Push on a freight train (or a feather) to increase its speed, and the resistance you feel reflects its mass. At a microscopic level, the freight train’s mass comes from its constituent 10 molecules and atoms, which are themselves built from fundamental particles, electrons and quarks. But where do the masses of these and other fundamental particles come from? When physicists in the 1960s modeled the 15 behavior of these particles using equations rooted in quantum physics, they encountered a puzzle. If they imagined that the particles were all massless, then each term in the equations clicked into a perfectly symmetric pattern, like the tips of a perfect 20 snowflake. And this symmetry was not just mathematically elegant. It explained patterns evident in the experimental data. But—and here’s the puzzle—physicists knew that the particles did have mass, and when they modified the equations to 25 account for this fact, the mathematical harmony was spoiled. The equations became complex and unwieldy and, worse still, inconsistent. What to do? Here’s the idea put forward by Higgs. Don’t shove the particles’ masses down the throat of 30 the beautiful equations. Instead, keep the equations pristine and symmetric, but consider them operating within a peculiar environment. Imagine that all of space is uniformly filled with an invisible substance—now called the Higgs field—that exerts a 35 drag force on particles when they accelerate through it. Push on a fundamental particle in an effort to increase its speed and, according to Higgs, you would feel this drag force as a resistance. Justifiably, you would interpret the resistance as the particle’s mass. 40 For a mental toehold, think of a ping-pong ball submerged in water. When you push on the ping-pong ball, it will feel much more massive than it does outside of water. Its interaction with the watery environment has the effect of endowing it with mass. 45 So with particles submerged in the Higgs field. In 1964, Higgs submitted a paper to a prominent physics journal in which he formulated this idea mathematically. The paper was rejected. Not because it contained a technical error, but because the 50 premise of an invisible something permeating space, interacting with particles to provide their mass, well, it all just seemed like heaps of overwrought speculation. The editors of the journal deemed it “of no obvious relevance to physics.” 55 But Higgs persevered (and his revised paper appeared later that year in another journal), and physicists who took the time to study the proposal gradually realized that his idea was a stroke of genius, one that allowed them to have their cake and eat it 60 too. In Higgs’s scheme, the fundamental equations can retain their pristine form because the dirty work of providing the particles’ masses is relegated to the environment. While I wasn’t around to witness the initial 65 rejection of Higgs’s proposal in 1964 (well, I was around, but only barely), I can attest that by the mid-1980s, the assessment had changed. The physics community had, for the most part, fully bought into the idea that there was a Higgs field permeating 70 space. In fact, in a graduate course I took that covered what’s known as the Standard Model of Particle Physics (the quantum equations physicists have assembled to describe the particles of matter and the dominant forces by which they influence 75 each other), the professor presented the Higgs field with such certainty that for a long while I had no idea it had yet to be established experimentally. On occasion, that happens in physics. Mathematical equations can sometimes tell such a convincing tale, 80 they can seemingly radiate reality so strongly, that they become entrenched in the vernacular of working physicists, even before there’s data to confirm them.

After reading the passage choose the best answer to the given question based on what is stated or implied in the passage and in any accompanying graphics (such as a table or graph).

Nearly a half-century ago, Peter Higgs and a handful of other physicists were trying to understand the origin of a basic physical feature: mass. You can think of mass as an object’s heft or, a little more 5 precisely, as the resistance it offers to having its motion changed. Push on a freight train (or a feather) to increase its speed, and the resistance you feel reflects its mass. At a microscopic level, the freight train’s mass comes from its constituent 10 molecules and atoms, which are themselves built from fundamental particles, electrons and quarks. But where do the masses of these and other fundamental particles come from? When physicists in the 1960s modeled the 15 behavior of these particles using equations rooted in quantum physics, they encountered a puzzle. If they imagined that the particles were all massless, then each term in the equations clicked into a perfectly symmetric pattern, like the tips of a perfect 20 snowflake. And this symmetry was not just mathematically elegant. It explained patterns evident in the experimental data. But—and here’s the puzzle—physicists knew that the particles did have mass, and when they modified the equations to 25 account for this fact, the mathematical harmony was spoiled. The equations became complex and unwieldy and, worse still, inconsistent. What to do? Here’s the idea put forward by Higgs. Don’t shove the particles’ masses down the throat of 30 the beautiful equations. Instead, keep the equations pristine and symmetric, but consider them operating within a peculiar environment. Imagine that all of space is uniformly filled with an invisible substance—now called the Higgs field—that exerts a 35 drag force on particles when they accelerate through it. Push on a fundamental particle in an effort to increase its speed and, according to Higgs, you would feel this drag force as a resistance. Justifiably, you would interpret the resistance as the particle’s mass. 40 For a mental toehold, think of a ping-pong ball submerged in water. When you push on the ping-pong ball, it will feel much more massive than it does outside of water. Its interaction with the watery environment has the effect of endowing it with mass. 45 So with particles submerged in the Higgs field. In 1964, Higgs submitted a paper to a prominent physics journal in which he formulated this idea mathematically. The paper was rejected. Not because it contained a technical error, but because the 50 premise of an invisible something permeating space, interacting with particles to provide their mass, well, it all just seemed like heaps of overwrought speculation. The editors of the journal deemed it “of no obvious relevance to physics.” 55 But Higgs persevered (and his revised paper appeared later that year in another journal), and physicists who took the time to study the proposal gradually realized that his idea was a stroke of genius, one that allowed them to have their cake and eat it 60 too. In Higgs’s scheme, the fundamental equations can retain their pristine form because the dirty work of providing the particles’ masses is relegated to the environment. While I wasn’t around to witness the initial 65 rejection of Higgs’s proposal in 1964 (well, I was around, but only barely), I can attest that by the mid-1980s, the assessment had changed. The physics community had, for the most part, fully bought into the idea that there was a Higgs field permeating 70 space. In fact, in a graduate course I took that covered what’s known as the Standard Model of Particle Physics (the quantum equations physicists have assembled to describe the particles of matter and the dominant forces by which they influence 75 each other), the professor presented the Higgs field with such certainty that for a long while I had no idea it had yet to be established experimentally. On occasion, that happens in physics. Mathematical equations can sometimes tell such a convincing tale, 80 they can seemingly radiate reality so strongly, that they become entrenched in the vernacular of working physicists, even before there’s data to confirm them.

After reading the passage choose the best answer to the given question based on what is stated or implied in the passage and in any accompanying graphics (such as a table or graph).

Nearly a half-century ago, Peter Higgs and a handful of other physicists were trying to understand the origin of a basic physical feature: mass. You can think of mass as an object’s heft or, a little more 5 precisely, as the resistance it offers to having its motion changed. Push on a freight train (or a feather) to increase its speed, and the resistance you feel reflects its mass. At a microscopic level, the freight train’s mass comes from its constituent 10 molecules and atoms, which are themselves built from fundamental particles, electrons and quarks. But where do the masses of these and other fundamental particles come from? When physicists in the 1960s modeled the 15 behavior of these particles using equations rooted in quantum physics, they encountered a puzzle. If they imagined that the particles were all massless, then each term in the equations clicked into a perfectly symmetric pattern, like the tips of a perfect 20 snowflake. And this symmetry was not just mathematically elegant. It explained patterns evident in the experimental data. But—and here’s the puzzle—physicists knew that the particles did have mass, and when they modified the equations to 25 account for this fact, the mathematical harmony was spoiled. The equations became complex and unwieldy and, worse still, inconsistent. What to do? Here’s the idea put forward by Higgs. Don’t shove the particles’ masses down the throat of 30 the beautiful equations. Instead, keep the equations pristine and symmetric, but consider them operating within a peculiar environment. Imagine that all of space is uniformly filled with an invisible substance—now called the Higgs field—that exerts a 35 drag force on particles when they accelerate through it. Push on a fundamental particle in an effort to increase its speed and, according to Higgs, you would feel this drag force as a resistance. Justifiably, you would interpret the resistance as the particle’s mass. 40 For a mental toehold, think of a ping-pong ball submerged in water. When you push on the ping-pong ball, it will feel much more massive than it does outside of water. Its interaction with the watery environment has the effect of endowing it with mass. 45 So with particles submerged in the Higgs field. In 1964, Higgs submitted a paper to a prominent physics journal in which he formulated this idea mathematically. The paper was rejected. Not because it contained a technical error, but because the 50 premise of an invisible something permeating space, interacting with particles to provide their mass, well, it all just seemed like heaps of overwrought speculation. The editors of the journal deemed it “of no obvious relevance to physics.” 55 But Higgs persevered (and his revised paper appeared later that year in another journal), and physicists who took the time to study the proposal gradually realized that his idea was a stroke of genius, one that allowed them to have their cake and eat it 60 too. In Higgs’s scheme, the fundamental equations can retain their pristine form because the dirty work of providing the particles’ masses is relegated to the environment. While I wasn’t around to witness the initial 65 rejection of Higgs’s proposal in 1964 (well, I was around, but only barely), I can attest that by the mid-1980s, the assessment had changed. The physics community had, for the most part, fully bought into the idea that there was a Higgs field permeating 70 space. In fact, in a graduate course I took that covered what’s known as the Standard Model of Particle Physics (the quantum equations physicists have assembled to describe the particles of matter and the dominant forces by which they influence 75 each other), the professor presented the Higgs field with such certainty that for a long while I had no idea it had yet to be established experimentally. On occasion, that happens in physics. Mathematical equations can sometimes tell such a convincing tale, 80 they can seemingly radiate reality so strongly, that they become entrenched in the vernacular of working physicists, even before there’s data to confirm them.

After reading the passage choose the best answer to the given question based on what is stated or implied in the passage and in any accompanying graphics (such as a table or graph).

Nearly a half-century ago, Peter Higgs and a handful of other physicists were trying to understand the origin of a basic physical feature: mass. You can think of mass as an object’s heft or, a little more 5 precisely, as the resistance it offers to having its motion changed. Push on a freight train (or a feather) to increase its speed, and the resistance you feel reflects its mass. At a microscopic level, the freight train’s mass comes from its constituent 10 molecules and atoms, which are themselves built from fundamental particles, electrons and quarks. But where do the masses of these and other fundamental particles come from? When physicists in the 1960s modeled the 15 behavior of these particles using equations rooted in quantum physics, they encountered a puzzle. If they imagined that the particles were all massless, then each term in the equations clicked into a perfectly symmetric pattern, like the tips of a perfect 20 snowflake. And this symmetry was not just mathematically elegant. It explained patterns evident in the experimental data. But—and here’s the puzzle—physicists knew that the particles did have mass, and when they modified the equations to 25 account for this fact, the mathematical harmony was spoiled. The equations became complex and unwieldy and, worse still, inconsistent. What to do? Here’s the idea put forward by Higgs. Don’t shove the particles’ masses down the throat of 30 the beautiful equations. Instead, keep the equations pristine and symmetric, but consider them operating within a peculiar environment. Imagine that all of space is uniformly filled with an invisible substance—now called the Higgs field—that exerts a 35 drag force on particles when they accelerate through it. Push on a fundamental particle in an effort to increase its speed and, according to Higgs, you would feel this drag force as a resistance. Justifiably, you would interpret the resistance as the particle’s mass. 40 For a mental toehold, think of a ping-pong ball submerged in water. When you push on the ping-pong ball, it will feel much more massive than it does outside of water. Its interaction with the watery environment has the effect of endowing it with mass. 45 So with particles submerged in the Higgs field. In 1964, Higgs submitted a paper to a prominent physics journal in which he formulated this idea mathematically. The paper was rejected. Not because it contained a technical error, but because the 50 premise of an invisible something permeating space, interacting with particles to provide their mass, well, it all just seemed like heaps of overwrought speculation. The editors of the journal deemed it “of no obvious relevance to physics.” 55 But Higgs persevered (and his revised paper appeared later that year in another journal), and physicists who took the time to study the proposal gradually realized that his idea was a stroke of genius, one that allowed them to have their cake and eat it 60 too. In Higgs’s scheme, the fundamental equations can retain their pristine form because the dirty work of providing the particles’ masses is relegated to the environment. While I wasn’t around to witness the initial 65 rejection of Higgs’s proposal in 1964 (well, I was around, but only barely), I can attest that by the mid-1980s, the assessment had changed. The physics community had, for the most part, fully bought into the idea that there was a Higgs field permeating 70 space. In fact, in a graduate course I took that covered what’s known as the Standard Model of Particle Physics (the quantum equations physicists have assembled to describe the particles of matter and the dominant forces by which they influence 75 each other), the professor presented the Higgs field with such certainty that for a long while I had no idea it had yet to be established experimentally. On occasion, that happens in physics. Mathematical equations can sometimes tell such a convincing tale, 80 they can seemingly radiate reality so strongly, that they become entrenched in the vernacular of working physicists, even before there’s data to confirm them.

After reading the passage choose the best answer to the given question based on what is stated or implied in the passage and in any accompanying graphics (such as a table or graph).

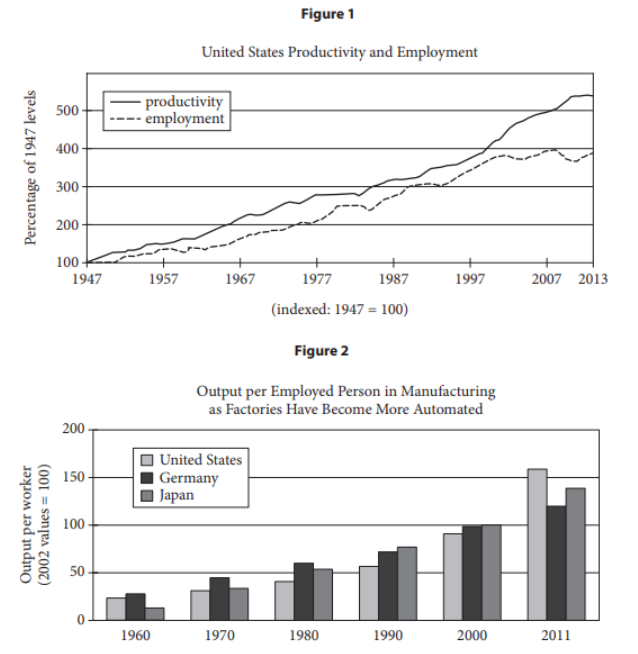
MIT business scholars Erik Brynjolfsson and Andrew McAfee have argued that impressive advances in computer technology—from improved industrial robotics to automated translation 5 services—are largely behind the sluggish employment growth of the last 10 to 15 years. Even more ominous for workers, they foresee dismal prospects for many types of jobs as these powerful new technologies are increasingly adopted not only 10 in manufacturing, clerical, and retail work but in professions such as law, financial services, education, and medicine. That robots, automation, and software can replace people might seem obvious to anyone who’s worked 15 in automotive manufacturing or as a travel agent. But Brynjolfsson and McAfee’s claim is more troubling and controversial. They believe that rapid technological change has been destroying jobs faster than it is creating them, contributing to the 20 stagnation of median income and the growth of inequality in the United States. And, they suspect, something similar is happening in other technologically advanced countries. As evidence, Brynjolfsson and McAfee point to a 25 chart that only an economist could love. In economics, productivity—the amount of economic value created for a given unit of input, such as an hour of labor—is a crucial indicator of growth and wealth creation. It is a measure of progress. On the 30 chart Brynjolfsson likes to show, separate lines represent productivity and total employment in the United States. For years after World War II, the two lines closely tracked each other, with increases in jobs corresponding to increases in productivity. The 35 pattern is clear: as businesses generated more value from their workers, the country as a whole became richer, which fueled more economic activity and created even more jobs. Then, beginning in 2000,the lines diverge; productivity continues to rise robustly, 40 but employment suddenly wilts. By 2011, a significant gap appears between the two lines, showing economic growth with no parallel increase in job creation. Brynjolfsson and McAfee call it the “great decoupling.” And Brynjolfsson says he is 50 confident that technology is behind both the healthy growth in productivity and the weak growth in jobs. It’s a startling assertion because it threatens the faith that many economists place in technological progress. Brynjolfsson and McAfee still believe that technology boosts productivity and makes societies wealthier, but they think that it can also have a dark side: technological progress is eliminating the need for many types of jobs and leaving the typical worker worse off than before. Brynjolfsson can point to a 55 second chart indicating that median income is failing to rise even as the gross domestic product soars. “It’s the great paradox of our era,” he says. “Productivity is at record levels, innovation has never been faster, and yet at the same time, we have a falling  edian 60 income and we have fewer jobs. People are falling behind because technology is advancing so fast and our skills and organizations aren’t keeping up.” While technological changes can be painful for workers whose skills no longer match the needs of 65 employers, Lawrence Katz, a Harvard economist, says that no historical pattern shows these shifts leading to a net decrease in jobs over an extended period. Katz has done extensive research on  how technological advances have affected jobs over the 70 last few centuries—describing, for example, how highly skilled artisans in the mid-19th century were displaced by lower-skilled workers in factories. While it can take decades for workers to acquire the expertise needed for new types of employment, he 75 says, “we never have run out of jobs. There is no long-term trend of eliminating work for people. Over the long term, employment rates are fairly stable. People have always been able to create new jobs. People come up with new things to do.” 80 Still, Katz doesn’t dismiss the notion that there is something different about today’s digital technologies—something that could affect an even broader range of work. The question, he says, is whether economic history will serve as a useful 85 guide. Will the job disruptions caused by technology be temporary as the workforce adapts, or will we see a science-fiction scenario in which automated processes and robots with superhuman skills take over a broad swath of human tasks? Though Katz 90 expects the historical pattern to hold, it is “genuinely a question,” he says. “If technology disrupts enough, who knows what will happen?”