Physics Test - 1

A dynamo is a device which converts mechanical energy into electrical energy. A dynamo is an electrical generator that produces direct current with the use of a commutator. Dynamos were the first electrical generators capable of delivering power for industry, and the foundation upon which many other later electric-power conversion devices were based, including the electric motor, the alternating-current alternator, and the rotary converter. Today, the simpler alternator dominates large scale power generation, for efficiency, reliability and cost reasons. A dynamo has the disadvantages of a mechanical commutator.

Given,

\(L=3.3~ H\)

\(C=840 \times 10^{-12}~F\)

\(q_{0}=105 \times 10^{-6}~ C\)

The total energy in the circuit is:

\(U=\frac{1}{2} \frac{q_{o}^{2}}{C}\) ......(i)

Where \(q_{0}\) is the initial charge on the capacitor and \(U\) is the total energy in the circuit.

Substitute \(840 \times 10^{-12} F\) for \(C\) and \(105 \times 10^{-6} C\) for \(q_{0}\) in (i).

\(U=\frac{1}{2} \frac{\left(105 \times 10^{-6}\right)^{2}}{840 \times 10^{-12}}\)

\(U=\frac{1}{2} \frac{11025 \times 10^{-12}}{840 \times 10^{-12}}=6.56~ J\)

In general capacitance of parallel plate, the capacitor is given by:

\(\mathrm{C}=\frac{\mathrm{k} \epsilon_{0} \mathrm{A}}{\mathrm{~d}}\)

Where \(\mathrm{C}\) is capacitance, \(\mathrm{k}\) is the relative permittivity of dielectric material, \(\epsilon_{0}\) is the permittivity of free space constant, \(A\) is an area of plates and \(d\) is the distance between them.

Therefore, the capacitance of parallel plates is increased by the insertion of a dielectric material. Further, the capacitance is inversely proportional to the electric field between the plates, and hence the presence of the dielectric decreases the effective electric field.

Both the poles of the magnet experience a force due to magnetic field produced by wires W₁ and W₂

North pole experiences a force \(\mathrm{F}_{1}\) due to \(\mathrm{W}_{1}\), and \(\mathrm{F}_{2}\) due to \(\mathrm{W}_{2}\) shown in diagram. Similarly, south pole experience a force

\(\mathrm{F}_{1}\) due to \(\mathrm{W}_{2}\) and \(\mathrm{F}_{2}\) due to \(\mathrm{W}_{1}\).

From free body diagram of magnet, it is clear that magnet experiences a net force towards right and a torque in anti- clockwise direction.

For a satellite revolving in a circular orbit around the earth, the physical quantity that remains constant is its angular momentum. 

In planetary motion, the net external torque on the planet is zero. Therefore, angular momentum will remain constant.

Given,

Potential difference across \(R \left( V _{ R }\right)=12~ V\) and Potential difference across \(RL ( V )=20~ V\)

For a series LR circuit, the total potential difference of the circuit is given by,

\( V^{2}=V_{R}^{2}+V_{L}^{2}\)

\(V_{L}^{2}=V^{2}-V_{R}^{2}=(20)^{2}-(12)^{2}\)

\(V_{L}^{2}=400-144=256\)

\(V_{L}=16~ V\)

The full form of DC is direct current. It is the current flowing in the circuit with a constant potential difference. If the resistance of the circuit is \(R\), the voltage of the \(D C\) source (e.g. a battery) is \({V}\), then the relation between \({V}, {R}\) and the current i flowing in the circuit is given by ohm's law i.e.,

\(V=i R\) Consider the circuit as shown below:

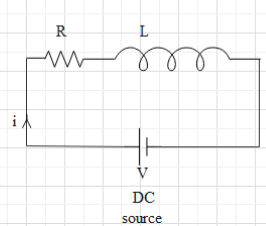
It is given that the voltage of the DC source is \(100\) volt and the current flowing in the circuit is 1 amp, so the resistance \(R\) of the circuit, according to ohm's law will

\(R=\frac{V}{i}=\frac{100}{1}=100 \Omega\). Therefore, the given circuit,

Which consists of a solenoid has a resistance of \(100 \Omega\).

The full form of \(A C\) is alternating current. When a source produces an oscillating potential difference across the circuit, an alternating (oscillating current) flows in the circuit and this type of circuit is called an AC circuit. Since it is an oscillating circuit, it has a frequency (f).

Now consider an AC circuit as shown below:

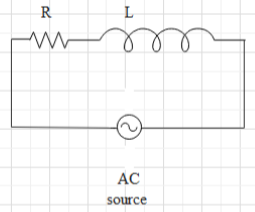
Like in a DC circuit, there is resistance (R) to resist the flowing charges (electrons), in an AC circuit also there is a resistance called impedance \((Z)\). The relation between the potential difference (V), current (i) and the impedance (Z) of the circuit is \(V=i Z\)......(1)

Therefore, impedance has the same unit as resistance i.e. \(\Omega\)

If the circuit consists of an inductor (solenoid) of inductance \(L\) and ha some resistance \(R\), then the impedance of the \(A C\) circuit is \(Z=\sqrt{R^{2}+(\omega L)^{2}}\)........(2)

Let us now calculate the impedance of the circuit. From equation (1) we know

\(Z=\frac{V}{i}\)

Therefore,

\(Z=\frac{100}{0.5}=200 \Omega\)

Since, the same solenoid is the resistance of the circuit will be the same. Hence, \(R=100 \Omega\). Substitute the values of \(Z\) and \(R\) in equation (2).

\(\Rightarrow 200=\sqrt{(100)^{2}+(\omega L)^{2}} \)

\(\Rightarrow 40000=(100)^{2}+(\omega L)^{2} \)

\(\Rightarrow 40000=10000+(\omega L)^{2}\)

Therefore, 

\(\omega L=\sqrt{30000}=173.2 \Omega\)

We know \(\omega=2 \pi f\)

\(f=50 H z\) and \(\pi=3.14\).

This implies that:

\(\omega=2 \times 3.14 \times 50=314 {~s}^{-1}\)

\(\therefore L=\frac{173.2}{314}=0.55 H\).

According to the first law of thermodynamics “heat always flows from higher temperature to lower temperature until they attain thermal equilibrium“ but this law holds for convection and conduction only in radiation the energy can transfer without any temperature difference and it is transferred in a form of E.M wave.

For example heat from the sun can’t reach earth directly through convection or conduction since there is no medium present, it’s been transferred through radiation since E.M wave doesn’t require a medium for propagation and neither it depends on the temperature difference between two objects.

Given,

Temperature of gas \((\mathrm{T})=300 \mathrm{~K}\), molar mass of Nitrogen \((\mathrm{M})=28 \mathrm{gm}/ \mathrm{mol}=28 \times 10^{-3} \mathrm{~kg} / \mathrm{mol}\)

We know,

The rms speed of molecules in a gas is given by:

\(V_{rms}=\sqrt{\frac{3RT}{M}}\)

\(V_{rms}=\sqrt{\frac{3\times 8.3 \times 300}{28\times 10^{-3}}}=\sqrt{266785.714}\)\)

= \(516.5{\mathrm{m}}/{\mathrm{s}}\)

\(\therefore\) The rms speed of nitrogen in gas at  \(300\mathrm{~K}\) is \(516\mathrm{~m}/\mathrm{s}\).

When two waves having small differences in their frequency superpose each other there is a periodic variation in the intensity of the sound i.e., the amplitude of the sound rises and falls. The number of such variations heard per second is called the beat frequency.

The beat frequency is given by,

\(v_{B E A T}=v_{1}-v_{2} \ldots(1)\), 

Where \(\mathrm{v}_{1}\) and \(\mathrm{v}_{2}\) are the frequency of the two waves that are superposed.

In the question, the wavelengths of the two superposing waves are given to us. Let us write the wavelength in terms of their frequency using equation (1).

\(v_{1}=\frac{\mathrm{V}}{2 }\) and \(v_{2}=\frac{\mathrm{V}}{2.02 \mathrm{}}\) the velocity of both the waves i.e., \(\mathrm{V}\) is the same since they are moving together.

Now let us substitute the frequency of both the waves in equation 2 to determine the velocity of the wave.

\(v_{B E A T}=v_{1}-v_{2} \)

\(\Rightarrow v_{B E A T}=\frac{V}{2}-\frac{V}{2.02} \)

\(\Rightarrow 2=\operatorname{V}\left(\frac{1}{2}-\frac{1}{2.02}\right) \)

\(\Rightarrow 2=V(0.5-0.495049) \)

\(\Rightarrow V=\frac{2}{4.95 \times 10^{-3}}\)

\(=0.404 \times 10^{3}\)

\(=404 \mathrm{~m} / \mathrm{s}\)