Physics Test - 7

Given \(T_1=8 T_2\) and \(Z=1\) (for hydrogen)

We know that the time period for the electron moving in the \(n ^{\text {th }}\) orbit is given as,

\(\Rightarrow T_n=\frac{4 \epsilon_o^2 n^3 h^3}{m Z^2 e^4}\) ... (1)

Where \(\epsilon_0=\) permittivity, \(h =\) Planck's constant, \(m =\) mass of the electron, \(Z =\) atomic number and \(e =\) charge on the electron

By equation 1 , the time period of the electron in the hydrogen atom is given as (\(Z\) \(=1)\),

\( \Rightarrow T_n=\frac{4 \epsilon_o^2 n^3 h^3}{m \times 1^2 \times e^4} \)

\( \Rightarrow T_n \propto n^3\) ...(2)

By equation 2 ,

\( \Rightarrow T_1 \propto n_1^3 \) ...(3)

\( \Rightarrow T_2 \propto n_2^3\) ...(4)

By equation 3 and equation 4 ,

\( \Rightarrow \frac{T_1}{T_2}=\frac{n_1^3}{n_2^3} \)

\( \Rightarrow \frac{n_1^3}{n_2^3}=\frac{8 T_2}{T_2} \)

\( \Rightarrow \frac{n_1}{n_2}=\frac{2}{1}\)

\(\Rightarrow n _1=2 n _2\)

By equation 5 when \(n _2=2\),

\( \Rightarrow n _1=2 \times 2 \)

\( \Rightarrow n _1=4\)

Given,

\(\mathrm{L}=1 \mathrm{H}\) 

\(\mathrm{C}=\mathrm{2 0 \mu} \mathrm{F}=\mathrm{2 0} \times \mathrm{1 0}^{-6} \mathrm{F}\)

\(\mathrm{R}=\mathrm{3 0 0} \Omega\)

\(\nu=\frac{\mathrm{5 0}}{\pi} \mathrm{H} \mathrm{z}\)

The inductive reactance is, 

\(X_{L}=2 \pi \nu L\)

\(=2 \pi\left(\frac{50}{\pi}\right) \times 1\)

\(=100\) Ω

The capacitive reactance is, 

\(X_{C}=\frac{1}{2 \pi \nu C}\)

\(=\frac{1}{2 \pi\left(\frac{50}{\pi}\right) 20 \times 10^{-6}}\)

\(=500\) Ω

The impedance of the series LCR cicuit is, 

\(Z=\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}\)

\(Z=\sqrt{(300)^{2}+(400)^{2}}\)

\(=500\) Ω

For the same insulation by the brick and cement \(Q, A\left(T_{1}-T_{2}\right)\) and \(t\) do not change.

Thus, \(\frac{K}{L}\) will remain constant.

If \({K}_{1}\) and \({K}_{2}\) be the thermal conductivity of brick and cement respectively \(\mathrm{L}_{1}\) and \(\mathrm{L}_{2}\) be the required thickness then,

\(\frac{K_{1}}{L_{1}}=\frac{K_{2}}{L_{2}}\)

\(\Rightarrow \frac{0.6}{L_{1}}=\frac{0.13}{5} \)

\(\Rightarrow L_{1}=23.07 \mathrm{~cm}\)

Thus, the correct anwer is \(23 \mathrm{~cm}\).

The electric field of a hollow spherical capacitor is localized in between the inner and outer surfaces of the spherical conductor. Therefore, at point $r_1 < r < r_2$, the electric field will not be zero.

Given:

Output power \(\mathrm{P}=100 \mathrm{~W}\)

Voltage across primary \(\mathrm{V}_{\mathrm{p}}=220 \mathrm{~V}\)

Current in the primary \(\mathrm{I}_{\mathrm{p}}=0.5 \mathrm{~A}\)

Efficiency of a transformer:

\(\eta=\frac{\text { output power }}{\text { input power }} \times 100\) \(=\frac{P}{V_{p} I_{p}} \times 100\)

\(=\frac{100}{220 \times 0.5} \times 100=90.90 \%\)

For a given ideal gas the sound speed depends only on its temperature. At a constant temperature, the ideal gas pressure and density have no effect on the speed of sound, because pressure and density (also proportional to pressure) have equal but opposite effects on the speed of sound.

Here,

\(\frac{N}{N_{0}}=\frac{6.25}{100}\)

\(=\frac{0.25}{4}\)

\(t=1\) days, \(\lambda=?\)

As,

\(\frac{N}{N_{0}}=\left(\frac{1}{2}\right)^{n}\)

\(=\frac{0.25}{4}\)

\(=\frac{1}{16}\)

\(=\left(\frac{1}{2}\right)^{4}\)

\(\therefore n=4\)

As,

\(n=\frac{t}{T}= T\)

\(=\frac{t}{n}\)

\(=\frac{16}{4}\)

\(=4\) days

Decay constant,

\(\lambda=\frac{0.693}{T}=\frac{0.693}{4}\)

\(=0.173\) days\(^{-1}\)

We know that the momentum is conserved to apply the conservation of momentum in

the X-direction.

\(m v=m v_{1} \cos \theta\)

\(v=v_{1} \cos \theta \ldots \ldots\) (1)

We will now apply the conservation of momentum in the Y direction. \(0=\frac{m v}{\sqrt{3}}-m v_{1} \sin \theta\)

\(\frac{v}{\sqrt{3}}=v_{1} \sin \theta \ldots \ldots(2)\)

Now squaring and adding equation (1) and (2), we get, \(v^{2}+\frac{v^{2}}{(\sqrt{3})^{2}}=v_{1}^{2} \cos ^{2} \theta+v_{1}^{2} \sin ^{2} \theta\)

\(\frac{4 v^{2}}{3}=v_{1}^{2}\left(\cos ^{2} \theta+\sin ^{2} \theta\right)\)

We know that \(\left(\cos ^{2} \theta+\sin ^{2} \theta\right)=1\), therefore the above equation becomes,

\(\frac{4 v^{2}}{3}=v_{1}^{2}\)

\(v_{1}=\frac{2 v}{\sqrt{3}}\)

Assume that mass of an equilateral triangle is concentrated about its vertices and first determine the moment of inertia of the entire lamina by finding the distance between the lamina’s centre and its vertices. Then determine the moment of inertia of the triangle DEF that is cut out, using the same assumption about mass concentrated at its own vertices and arrive at an expression for it in terms of the moment of inertia of the entire lamina. To this end, calculate the difference between the two moments of inertia thus obtained to arrive at the appropriate result for the rest of the lamina.

Formula Used:

Moment of inertia \(I=\Sigma m r^{2}\)

Let the length of the sides of the equilateral triangular lamina \(\mathrm{ABC}\) be \(a\), and let the mass of the entire lamina

be \(m\). Assuming that the mass of the lamina is concentrated about its vertices, the distance of the axis of rotation from the massive vertices can be found.

Let the distance of the axis of rotation \(\mathrm{O}\) to one of the vertices \(\mathrm{A}\) be \(\mathrm{OA}\), as shovn in the figure. Since \(\triangle A B C\) is equilateral, vie have \(\angle C A B=60^{\circ}\). The line drawn from \(\mathrm{O}\) to \(\mathrm{A}\) bisects this angle in such a way that,

\(\angle O A D=30^{\circ}\)

From right-angled \(\triangle O A D\), we have:

\(\cos 30^{\circ}=\frac{A D}{O A}\)

\(\Rightarrow O A=\frac{A D}{\cos 30^{\circ}}=\frac{\left(\frac{a}{2}\right)}{\left(\frac{\sqrt{3}}{2}\right)}=\frac{a}{\sqrt{3}}\)

Therefore, the moment of inertia \(I_{0}\) of the lamina acting about its centre due to all 3 of its massive vertices,

with an axis perpendicular to its plane can be given as:

\(I_{0}=\Sigma m r^{2}=3 \times m(O A)^{2}\)

\(=3 \times m \times\left(\frac{a}{\sqrt{3}}\right)^{2}\)

\(=3 \times \frac{m a^{2}}{3}=m a^{2}\)

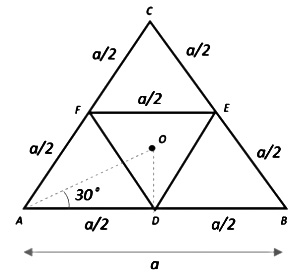
Now, we are given that a cavity DEF is cut from the lamina in such a way that the points \(D, E\) and \(F\) are the midpoints of sides \(\mathrm{AB}, \mathrm{BC}\) and \(\mathrm{AC}\) respectively as shown. This divides the lamina into 4 equilateral triangles such that each equilateral triangle has a mass of:

\(m^{\prime}=\frac{m}{4}\)

We now find the moment of inertia of \(\Delta D E F\) about the same axis of rotation, as we did for the entire lamina. Let the distance of the axis of rotation from one of the vertices of DEF be OD.

From \(\triangle A O D\) we have:

\(\sin 30^{\circ}=\frac{O D}{O A}\)

\(\Rightarrow O D=\sin 30^{\circ} \times O A=\frac{1}{2} \times \frac{a}{\sqrt{3}}=\frac{a}{2 \sqrt{3}}\)

Therefore, the moment of inertia of the equilateral triangle DEF due to all 3 of its massive vertices will be:

\(I^{\prime}=3 \times m^{\prime}(O D)^{2}=3 \times \frac{m}{4} \times\left(\frac{a}{2 \sqrt{3}}\right)^{2}\)

\(\Rightarrow I^{\prime}=3 \times \frac{m}{4} \times \frac{a^{2}}{12}=3 \times \frac{1}{48} \times m a^{2}=\frac{1}{16} \times m a^{2}\)

But we know that \(I_{0}=m a^{2}\),

Therefore, \(I^{\prime}=\frac{1}{16} \times I_{0}=\frac{I_{0}}{16}\)

Once this part is removed from the lamina, the moment of inertia of the remaining part of the lamina about the same axis will be:

\(I=I_{0}-I^{\prime}=I_{0}-\frac{I_{0}}{16}=\frac{16 I_{0}-I_{0}}{16}=\frac{15 I_{0}}{16}\)

Bohr model: In 1913 , Niels Bohr gave the Bohr's atom model which retained essential features of Rutherford's model and at the same time took into account its drawbacks.

The electrons revolve around the nucleus in circular orbits which is called the stationary orbit.

According to Bohr's atom model, the electrons of an atom revolve around the nucleus only in those orbits in which the angular momentum of the electron is an integral multiple of \(\frac{h}{2 \pi}\).

By absorbing energy the electrons are able to jump from lower energy( \(E_{i}\) ) level to higher energy level (\(E_{f}\) ) and vice versa.

The energy of emitted radiation is given by:

\(h v=E_{F}-E_{i}\)

The energy of electrons in any orbit is given by:

\(E_{n}=-13.6 \frac{Z^{2}}{n^{2}} \mathrm{eV}\)

Where \(\mathrm{n}\) is the principal quantum number and \(Z\) is the atomic number.

The ionization energy of the hydrogen atom in the excited state means the atom is already in the first excited state and n = 2

The energy of the electron in any excited state is given by:

\(E_{n}=-13.6 \frac{Z^{2}}{n^{2}} \mathrm{eV}\)

The above equation can be written for the excited state of the hydrogen atom as

\(\therefore E_{n}=\frac{-13.6}{2^{2}} \mathrm{eV}=-3.4 \mathrm{eV}\)