CBSE Class 12 Maths 2024-25: Chapter 7 Integrals Important Competency-Based Questions with Answers; Download Free PDF

As the CBSE Class 12 board exams get closer, students need to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.

This article explores Chapter 7 Integrals highlights key competency-based questions and provides answers to help students succeed.

Understanding Competency-Based Questions in Chapter 7 Integrals

Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.

These questions are different from regular memorization. They encourage students to think critically and solve problems, helping them understand the concepts in Chapter 7 Integrals better.

CBSE Class 12 Maths Chapter 7 Integrals Important Competency-Based Questions

Q.1 Look at the integral given below

Answer. (2)

Q.2 What is the value of the following integral?

Answer. (2)

Q.3 Varath says the following:

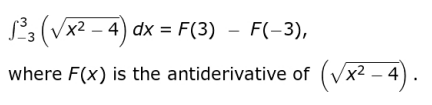
Which of the following can be said about Varath's statement?

1. It is true, as the function is continuous in [-3,3].
2. It is true, as per the fundamental theorem of calculus.
3. It is false, as the integral is not defined over the interval.
4. It is false, as the antiderivative of any function within a square root does not exist in R

Answer. (3)

Q.4 Mr. Dinesh writes the following expression on the blackboard:

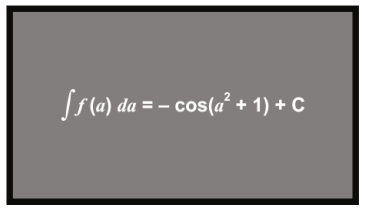
He asked his students to determine the function that he integrated.

Sameer says, "sin(a² + 1)".
Danish says, "-sin(a² + 1)".
Meera says, "2 a sin( a² + 1)".
Deepa says, "-2 a sin( a² + 1)".

Who is correct?

1. Sameer
2. Danish
3. Meera
4. Deepa

Answer. (3)

Download PDF
CBSE Class 12 Maths Chapter 1: Relations and Functions Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 2 : Inverse Trigonometric Functions Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 3 : Matrices Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 4: Determinants Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 5: Continuity & Differentiability Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 6: Application of Derivatives Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 7: Integrals Important Competency-Based Questions	Click Here

Q.5 Read the statements independently and carefully and then choose the option that correctly describes them.

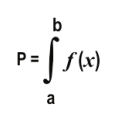
Statement 1: If the function f ( x ) is well defined and continuous in the interval (a, b), then P is always positive.

Statement 2: If P exists, then the function f ( x ) is always continuous in the interval (a, b).

1. Statement 1 is true but Statement 2 is false
2. Statement 1 is false but Statement 2 is true
3. Both Statement 1 and Statement 2 are true
4. Both Statement 1 and Statement 2 are false

Answer. (2)

Q.6 g(x) + C is an integral of h ( x ), where C is an arbitrary constant.

log_e (2 x + g² ( x )) + C is an integral of which of the following?

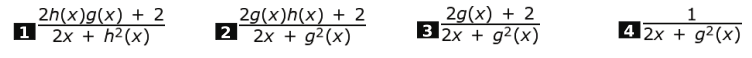
Answer. (2)

Q.7 Look at the integral given below and find f ( x ). Show your steps.

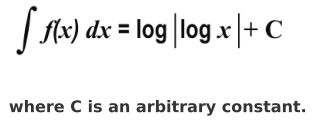
Answer.

Q.8 If g ( x ) is a polynomial function, find:

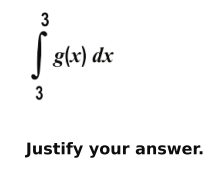
Answer. Writes the value of the definite integral as 0.

Writes that, since we are integrating the function from x = 3 to x = 3, the area under the function will be zero.

(Award full marks for any other valid justification.)

Q.9 Solve

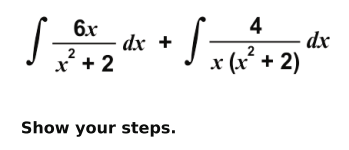
Answer. Rewrites the integral as:

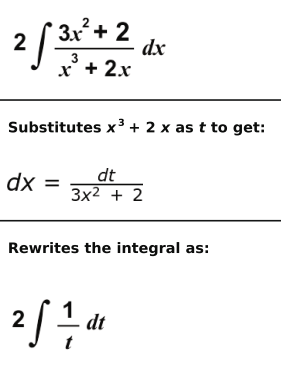
Integrates the above expression and gets 2log | t | + C as the solution where C is an arbitrary constant.

Substitutes t as x³ + 2 x to get 2log | x³ + 2 x | + C as the solution.

Q.10 Shown below is the first step of solving an integral.

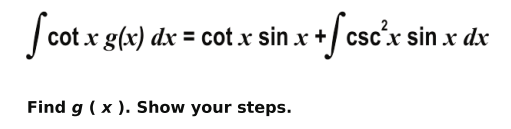
Answer. Compares the integral with the standard form of integration by parts to conclude:

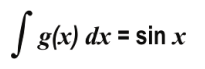
Uses the above step to find g ( x ) as cos x or cos (2 n + x) where n is a whole number.

Q.11 Integrate

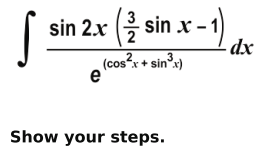
Answer. Substitutes (cos² x + sin³ x ) as t and finds dt as follows:

Q.12

Answer. Writes that Lalitha made an error in step 4.

Writes that Lalitha has integrated the expression given in step 3 as cosec e instead of -cosec 0.

Q.13 f(x) is a function such that:
f(x) + C = f(g(x) × h(x)) dx
where C is an arbitrary constant.

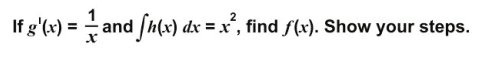
Answer. Writes that:

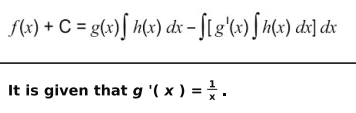
Integrates both sides of the above equation to get g ( x ) = log x + A where A is an arbitrary constant.

Q.14 Evaluate:

Answer.

Q.15 In the equation below, p, q, r and s are constants.

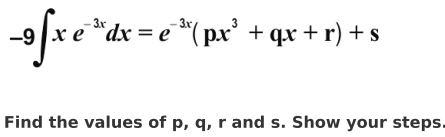
Answer.
Differentiates both sides of the given equation with respect to x to get:
-9 x (e -³x ) = (e ·³× )(3p x² + q) + (p x³ + q x + r)(-3e -³×)

Simplifies the above equation as:
-9 x (e -³x ) = (e ·³x )(-3p x3 + 3p x² - 3q x + q - 3r)

Equates the coefficients on both sides of the equation to find the values of p, q and r as 0, 3 and 1 respectively.

Writes that the constant, s cannot be uniquely determined from the given
information.

(Award full marks if the problem is solved by applying integration by parts to the LHS and then equating the coefficients on both sides.)

----

👉 CBSE Class 12 Study Materials

CBSE Class 12 Syllabus 2024-25	CBSE Class 12 Previous Year Papers
NCERT Books For Class 12 Books	NCERT Class 12 Solutions
CBSE Class 12 Full Study Material	CBSE Class 12 Sample Paper 2023-24