CBSE Class 10 Maths 2024-25: Chapter 3 Pair of Linear Equations in Two Variables Important Competency-Based Questions with Answers; Download Free PDF

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
As the CBSE Class 10 board exams get closer, it’s important for students to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.
This article explores Chapter 3 Pair of Linear Equations in Two Variable. It highlights key competency-based questions and provides answers to help students succeed.
Understanding Competency-Based Questions in Chapter 3: Pair of Linear Equations in Two Variable
Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.
Competency-based questions in Chapter 3: Pair of Linear Equations in Two Variable go beyond memorization, encouraging critical thinking and problem-solving. These questions help students grasp concepts deeply by applying them to real-world scenarios.
CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variable Important Competency-Based Questions
Multiple Choice Questions
Q.1 Given below is a graph showing two lines that never intersect. These are represented by two linear equations.
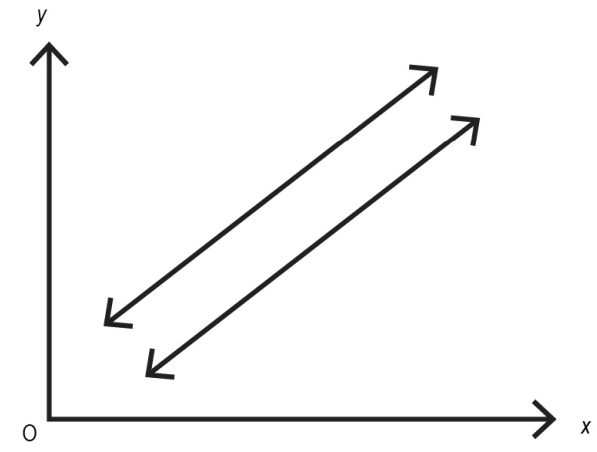
Which of these can be said about the number of solution(s) of the above pair of linear equations?
1. They have infinitely many solutions.
2. They have a unique solution.
3. They do not have a solution.
4. Nothing can be said about the number of solutions unless the algebraic form of these equations are known.
Answer. 3
Q.2 Given below is a pair of linear equations in two variables.
4 x + 2 y = 18
3 x - 6 y = 6
Which of the following pairs of equations have the same number of solution(s) as the given pair?
1. 3 a + 3 b = 18; a + b = 6
2. a - b = 4; b - a = 4
3. 6 a - 2 b = 10; 3 a + b = 5
4. 7 a + 9 b = 27; 28 a + 36 b = 76
Answer. 3
Q.3 If a pair of linear equations given by l1 x + m1 y + n1 = 0 and l2 x + m2 y + n2 = 0 has infinitely many solutions, then which of the following is DEFINITELY true?

Answer. 4
Q. 4 A gardener bought a mix of 100 flower and vegetable seeds for a total of Rs 1350. Each flower seed costs Rs 12, and each vegetable seed costs Rs 11.
Which of the following pairs of linear equations can be used to determine f , the number of flower seeds purchased, and v, the number of vegetable seeds purchased?
1. f + v = 100; 11 f + 12 v = 1350
2. f + v = 1350; 12 f + 11 v = 1350
3. f + v = 100; 12 f + 11 v = 1350
4. f + v = 23; 12 f + 11 v = 1350
Answer. 3
Q.5 Sara collected a total of Rs 1800 in a fundraising event. She knew that the event had a mix of Rs 10 and Rs 50 notes, but not sure how many of each. She counted the total number of notes as 60.
Which of the following pairs of linear equations can be used to find the number of 10-rupee and 50-rupee notes?
(Note: x represents the number of 10-rupee note and y represents the number of 50-rupee note.)
1. x + y = 60; x - y = 40
2. x + y = 1800; 10 x + 50 y = 60
3. x + y = 60; 10 y + 50 x = 1800
4. x + y = 60; 10 x + 50 y = 1800
Answer. 4
| Download PDF | |
| CBSE Class 10 Maths Chapter 1 Real Number: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 2 Polynomials: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variable: Important Competency-Based Questions | Click Here |
Q.6 Tanisha and Aditya have some chocolates with them such that:
♦ if Tanisha were to give 6 chocolates to Aditya, the new quantity of chocolates with each of them would be equal.
♦ instead, if Aditya were to give 3 chocolates to Tanisha, then Tanisha would have four times as many chocolates as Aditya initially had.
Which of these pairs of equations would help us find the number of chocolates that they have?
(Note: Assume the initial number of chocolates with Tanisha as 'x' and that with Aditya as 'y'.)
1. x - 6 = y + 6; x + 3 = 4( y - 3)
2. x - 6 = y + 6; x + 3 = 4 y
3. x + 6 = y - 6; x - 3 = 4 y
4. x - y = 6; x = y
Answer. 2
Assertion & Reason Type Questions
Q.7 For the given pair of linear equations, two statements are given below - one labelled Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
x - 2 y + 3 = 0
3 x + 4 y - 11 = 0
Assertion (A) : The pair of linear equations has a unique solution.
Reason (R) : The pair of linear equations represents a pair of coincident lines.
1. Both (A) and (R) are true and (R) is the correct explanation of the (A).
2. Both (A) and (R) are true but (R) is not the correct explanation of the (A).
3. (A) is true but (B) is false.
4. (A) is false but (B) is true.
Answer. 3
Free Response Questions
Q.8 Given below is a pair of linear equations in two variables:
6 y + 7 z = 12; 12 y - 12 z = 24
Which variable's coefficient can be changed such that the given pair has infinitely many solutions? What should it be changed to? Show your work.
Answer. Identifies that either of the coefficients of z can be changed.
Changes either 7 to (-6) in first equation or (-12) to 14 in second equation so that all 0.5 ratios are equal to 1/2 making it a pair with infinitely many solutions.
Q.9 On a specific day, a budget-friendly restaurant managed to sell 1000 vegetarian meals. These vegetarian meals were priced at Rs 85 per adult and Rs 45 per child. A total of Rs 73000 was collected from these sales.
If p represents the number of adult veg meals sold and q represents the number of child veg meals sold, write a pair of equations to find out how many meals of each kind were sold.
Answer .
Q.10 A pair of linear equations is shown below, where b is an integer.
2 x - y = b + 1
x + ( b - 1) y = 3 b
For any given value of b , how many solution(s) does this pair of equations have? Justify your answer.
Answer. Expresses equations in this or any equivalent form:
p + q = 1000
85 p + 45 q = 73000
Q.11 State true or false for the below statement and justify your answer
A pair of linear equations represented by intersecting lines can have two solutions.
Answer. States that the statement is false.
Gives the reason that a pair of linear equations represented by intersecting lines 0.5 have only one point of intersection on the lines, which is a unique solution.
Q.12 A pair of linear equations is shown below.
( k - 1) x + y = k + 1
( k 2 - 1) x + ( k + 1) y = 1 - k 2
If k > 1, then how many solutions does this pair of equations have?
Answer. Finds the ratio of the coefficients and concludes that there is no solution.

Case Study based Questions
Q.13 Represent the given situation with a pair of linear equations.
Answer. Assumes the price of one bowling alley ticket as Rs x and price of one movie ticket as 1 Rs y.
Frames the pair of linear equations as:
y - 2 x = 70
5 x + 3 y = 870
Q.14 Find the price of a movie ticket and a bowling alley ticket. Show your work.
Answer. Solves the equations simultaneously to find the price of a movie ticket as Rs 190 and 2 a bowling alley ticket as Rs 60.
Q.15 On the next day, Reena took her siblings to the mall. She observed that prices of the movie ticket and the bowling alley ticket had come back to their standard rates of Rs 220 and Rs 90, respectively. She bought a total of 10 tickets, costing her Rs 1420.
Find the number of movie tickets and bowling alley tickets she bought. Show your work.
Answer. Assumes the number of movie tickets and bowling alley tickets to be m and b 1 respectively.
Frames the pair of linear equations as:
m + b = 10
220 m + 90 b = 1420
Solves the equations to find the number of movie tickets ( m ) and bowling alley 1 tickets ( b ) to be 4 and 6 respectively.
👉 Read Also- CBSE Class 10 Half-Yearly/Mid Term 2024-25 : Most Important Questions with Answers; PDF Download (All Subjects)
👉 CBSE Class 10 Study Materials
| CBSE Class 10 Syllabus 2024-25 | NCERT Solutions For Class 10 |
| CBSE Class 10 Previous Year Question Papers | CBSE Class 10 Books |
| CBSE Class 10 Full Study Material | CBSE Class 10 Sample Paper |







 Profile
Profile Signout
Signout












 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










