CBSE Class 12 Maths 2024-25: Chapter 9 Differential Equations Competency-Based Questions with Answers; Download Free PDF

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
As the CBSE Class 12 board exams get closer, students need to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.
This article explores Chapter 9 Differential Equations highlights key competency-based questions and provides answers to help students succeed.
Understanding Competency-Based Questions in Chapter 9 Differential Equations
Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.
These questions are different from regular memorization. They encourage students to think critically and solve problems, helping them understand the concepts in Chapter 9 Differential Equations better.
CBSE Class 12 Maths Chapter 9 Differential Equations Important Competency-Based Questions
Multiple Choice Questions
Q.1 A differential equation has an order of 3 and a degree of 2. Which of the following could this differential equation be?
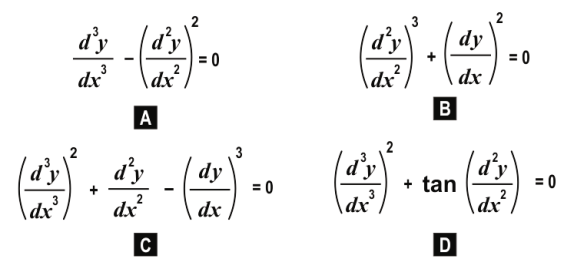
1. A
2. B
3. C
4. D
Answer. (3)
Q: 2 Look at the differential equation given below. What is its degree?
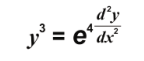
1. 1
2. 2
3. 3
4. 4
Answer. (1)
Q: 3 Shown below is a differential equation.

1. Expression 1
2. Expression 2
3. Expression 3
4. (the equation has no integrating factor as it is not a linear differential equation)
Answer. (3)
Q: 4 Which of the following differential equations will give y = sin x + cos x + C as the general solution where C is an arbitrary constant?
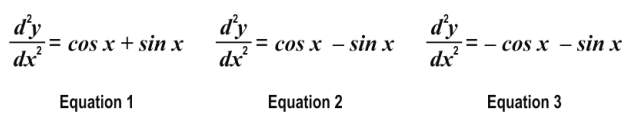
1. Equation 1
2. Equation 2
3. Equation 3
4. (cannot say without knowing the value of C)
Answer. (3)
Q: 5 Three friends - Bulbul, Ipsita and Sagarika were asked to find a particular solution of the following differential equation.
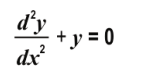
Shown below are their solutions.
Bulbul: y = sin x
Ipsita: y = cos x
Sagarika: y = sin x + cos x
Whose answer is correct?
1. only Bulbul
3. only Bulbul and Ipsita
2. only Sagarika
4. All Bulbul, Ipsita and Sagarika
Answer. (4)
| Download PDF | |
| CBSE Class 12 Maths Chapter 1: Relations and Functions Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 2 : Inverse Trigonometric Functions Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 3 : Matrices Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 4: Determinants Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 5: Continuity & Differentiability Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 6: Application of Derivatives Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 7: Integrals Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 8: Application of Integrals Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 9: Differential Equations Important Competency-Based Questions | Click Here |
Q: 6 Read the statements carefully and choose the option that correctly describes them.
Statement 1: The differential equation that represents the family of straight lines with slope 7 is given by y = 7 x + c, where c is an arbitrary constant.

1. Statement 1 is true but Statement 2 is false
2. Statement 1 is false but Statement 2 is true
3. Both Statement 1 and Statement 2 are true
4. Both Statement 1 and Statement 2 are false
Answer. (4)
Free Response Questions
Q.7 Sumit finds the general solution of the differential equation yy' = e 3x as

Did Sumit find the correct general solution? Show your work and justify.
Answer. Rewrites the given differential equation as ydy = e3x dx. Concludes that Sumit's general solution is incorrect by integrating both sides of the above equation to find the general solution as:

Q.8 The bottom valve of a conical tank is opened to remove sugarcane juice in a factory. The rate at which the juice pours out from the conical tank is directly proportional to the cube root of the rate of change of height of the juice present in the tank.
If k is the constant of proportionality, write a differential equation depicting the scenario.
Answer. Writes a differential equation that depicts the given scenario as:

Q.9 A differential equation is given below.
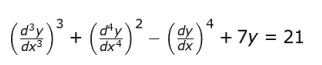
State whether the following statement is true or false. Justify your answer.
The degree of the given differential equation is equal to its order.
Answer. Writes that the statement is false
Gives a reason. For example, the order of the given differential equation is 4, but its degree is 2.
Q.10
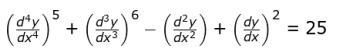
A differential equation is given above. State whether the following statement is true or false. Justify your answer.
The general solution of the given differential equation will have five arbitrary constants.
Answer. Writes that the statement is false
Gives a reason. For example, the number of arbitrary constants in the general solution of a differential equation is determined by its order, not its degree. Since the order of the given equation is 4, it will have only 4 arbitrary constants.
Q.11

Answer.

Solves the above equation to find the equation of the curve as follows:
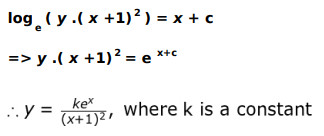
Q.12 In a controlled condition within a laboratory, a spherical balloon is being deflated at a rate proportional to its surface area at that instant. The spherical shape of the balloon is maintained throughout the process.
Form a differential equation that represents the rate of change of its radius. Show your work.
Answer. Takes V, S and r to be the volume, surface area and radius of the balloon at time t .
Writes that since the volume of the balloon is decreasing with time, the rate of change of its radius is negative.
Uses the given information and expresses the relationship between volume and surface area as:

Case Study
Answer the questions based on the given information.
The mixing tank shown below generates saline water (a mixture of salt and water) for the cooling of a thermoelectric power plant.
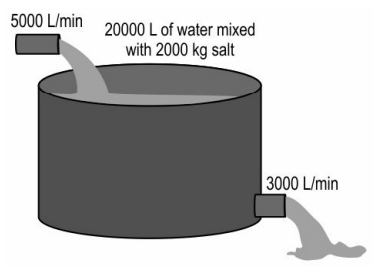
The tank initially holds 20000 L of water in which 2000 kg of salt has been dissolved. Then, pure water is poured into the tank at a rate of 5000 L per minute. The mixture in the tank, which is stirred continuously, flows out at a rate of 3000 L per minute.

Q.13 Find the expression for the rate of change of quantity of salt in the tank with time t . Show your work.
Answer. Uses the information given to find the rate of change of quantity of salt as follows:
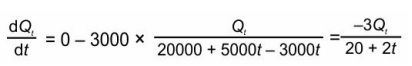
Q.14 Find the general solution of the differential equation corresponding to the rate of change of quantity of salt in the tank with time t . Show your work.
Answer. Separates the variables of the differential equation as follows:

Q.15 Use the initial conditions to determine the particular solution for the differential equation obtained. Show your work.
Answer. Takes initial condition Q t (0) = 2000 to obtain C as follows:
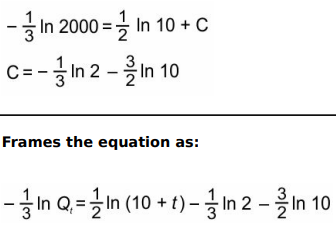
👉 Read Also - CBSE Class 12 Half-Yearly/Mid Term 2024-25 : Most Important Questions with Answers; PDF Download (All Subjects)
👉 Read Also - How CBSE’s New Exam Pattern Will Impact Class 11 and 12 Students
👉 CBSE Class 12 Study Materials
| CBSE Class 12 Syllabus 2024-25 | CBSE Class 12 Previous Year Papers |
| NCERT Books For Class 12 Books | NCERT Class 12 Solutions |
| CBSE Class 12 Full Study Material | CBSE Class 12 Sample Paper 2023-24 |







 Profile
Profile Signout
Signout












 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










