मध्य प्रदेश कक्षा-10वीं 2023 : गणित महत्वपूर्ण लघु उत्तरीय प्रश्‍न उत्तर के साथ; ये प्रश्‍न हर साल पूछता है

यहां गणित 10वी Exam 2023 के लिए New Blue Print पर आधारित  Most Important Question दिए गए है. ये प्रश्न (Question )Study Material के रूप में तैयार किये गए. जो आपके Paper के लिए बहुत महत्वपूर्ण है और ये Most Important Question तैयारी को और बेहतर बना सकते है I

Most Important Question

Q.1 समरूपता का क्या अर्थ है

उत्तर : समरूपता → वे आकृतियाँ जिनका आकार समान हो किन्तु विस्तार या माप या परिमाप अलग-अलग हो, समरूप कहलाती है। तथा उनका यह प्रगुण समरूपता कहलाता है।

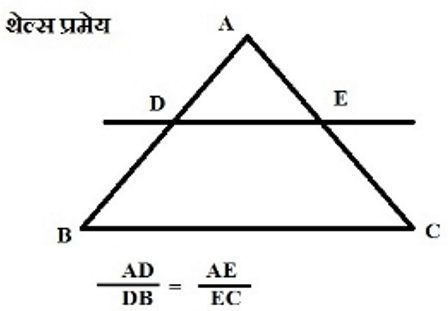
Q.2 आधारभूत आनुपातिक प्रमेय (थेल्स प्रमेय) का कथन लिखिए।

Ans : आधारभूत अनुपातिक प्रमेय (थेल्स प्रमेय) :

एक त्रिभुज की एक भुजा के समांतर खींची गयी रेखा अन्य दो भुजाओं को जिन दो बिन्दुओं पर प्रतिच्छेद करती है, वे बिन्दु भुजाओं को समान अनुपात में विभाजित करते हैं।

Q.3 निम्नलिखित मानों की माध्यिका ज्ञात कीजिए:

15, 35, 18, 26, 19, 25, 29, 20, 27

उत्तर : हल →
पदों को आरोही क्रम में रखने पर 15, 18, 19, 20, 25, 26, 27, 29, 35
पदों की संख्या = 9
मध्यिका = ((n+1)/2)वे पद का मान
= ((9+1)/2) वे पद का मान
= 5वे पद का मान
= 25

Q.4 एक सिक्के के एक बार उछाले जाने पर चित और पट एक साथ आने की प्रायिकता ज्ञात कीजिए।

उत्तर : हल →
प्रतिदर्श समष्टि S = {H,T}
n(S) = 2
चित पर एक साथ आने की प्रायिकता A = {……}
n(A) = 0
प्रायिकता P(A)=n(A) / n(S) = 0 /2

Q.5 माध्यिका के दो गुण एवं एक दोष लिखिए।

माध्य के गुण एवं दोष बताइए

उत्तर:

माध्यिका के गुण →

(1) इसकी गणना सरल है।
(2) यह सुपारिभाषित है।
(3) बड़े व छोटे पदो से यह प्रभावित नहीं होता।

माध्यिका के दोष →

(1) आंकड़ों को आरोही या अवरोही क्रम में व्यवस्थित करने में अतिरिक्त कार्य करना होता है।
(2) गणितीय गणनाओं के लिए उपयुक्त नहीं है।
(3) यह अनुमानित माध्य है।

Q.6 बहुभुज की समरूपता के लिये कौन-कौन से प्रतिबंध है?

उत्तर : बहुभुज की समरूपता के लिए प्रतिबंध →

(i)उनके संगत कोण बराबर हो और

(ii) उनकी संगत भुजाओं की लम्बाइयाँ आनुपातिक हों।

Q.7 समांतर माध्य की दो विशेषताएँ लिखिए।

उत्तर : हल →

समांतर माध्य की दो विशेषताएँ →

(1) इसके परिकलन में आँकड़ों को क्रमबद्ध करने की आवश्यकता नहीं होती है।

(2) इसे सरलता से अभिकलित किया जा सकता है।

Q.8 एक पाँसे को एक बार फेकने पर सम अंक आने की प्रायिकता ज्ञात कीजिए।

उत्तर : हल →

एक पासे को फेकने पर सम अंक आने की प्रायिकता निम्नानुसार ज्ञात की जा सकती है-
प्रतिदर्श समष्टि S = {1, 2, 3, 4, 5, 6}
n(S) = 6
सम अंक आने की घटना A = {2, 4, 6}
n(A) = 3
प्रायिकता = P(A)= n(A) / n(S) = 3 / 6 = 1 / 2

Q.9: 47, 53, 49, 60, 39, 42, 53, 52, 50, 55 का समांतर माध्य ज्ञात कीजिए।

Q.10 प्रतिस्थापन विधि द्वारा निम्नलिखित समीकरण निकाय को हल कीजिए:
x+y=7
3x-2y=11

उत्तर : हल→
x+y=7………(1)
3 x - 2 y =11……(2)
समीकरण (1) से
y=7 - x ……(3)
y का मान समीकरण (2) में रखने पर
3 x - 2 (7 - x ) = 11
3 x -14 + 2 x =11
3 x + 2 x = 11 + 14
5 x = 25
x = 25 / 5 = 5
x का मान समी. (3) में रखने पर
y=( 7 - 5 ) =2
अभीष्ट हल x = 5 एवं y = 2

Q.11 जाँच कीजिए कि क्या 6 से.मी. और 10 से.मी. समकोण त्रिभुज की भुजाएँ है?

उत्तर : हल→ दिया हैः सबसे बड़ी भुजा = 10 cm = कर्ण
(कर्ण) ² = (10)²= 100 ……… (1)
अब (लम्ब)² + (आधार)² = 8²+6²
= 64+36=100 ……… (2)
सभी (1) व (2) से
(कर्ण)²= (लम्ब)² + (आधार)²
त्रिभुज ABC समकोण त्रिभुज होगा।

Q.12: रिक्त स्थानों की पूर्ति कीजिए 1x5=5

(i) बेलन के आयतन का सूत्र ______ है।

(ii) किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग _______ है।

(iii) केन्द्रीय प्रवृत्ति के मापकों में एक आनुभाविक संबंध है:

3 माध्यक = बहुलक + ______

(iv) r त्रिज्यावाले वृत्त का क्षेत्रफल का सूत्र _______ है।

(v) किसी वृत्त की स्पर्श रेखा उसे ________ बिन्दु पर प्रतिच्छेद करती है।

उत्तर :
(i) π r ² h
(ii) 1
(iii)2 माध्य
(iv) π r ²
(v) स्पर्श बिंदु

Q.13: सत्य / असत्य लिखिए : : 1x5=5

(i) किसी बारंबारता बंटन में किसी वर्ग की संचयी बारंबारता उस वर्ग से पहले वाले सभी वर्गों की बारंबारताओं का योग होता है।

(ii) त्रिज्या r वाले वृत्त की परिधि = 2πr

(iii) घात 2 के किसी बहुपद के अधिक से अधिक दो शून्यक हो सकते हैं।

(iv) किसी बिंदु की y-अक्ष से दूरी उस बिन्दु का y निर्देशांक कहलाती है।

(v) √2 एक परिमेय संख्या है।

उत्तर :

(i) सत्य
(ii) सत्य
(iii)सत्य
(iv) असत्य
(v) असत्य

Q.14: एक वाक्य / शब्द में उत्तर दीजिए 1×5=5

(i) दृष्टि-रेखा की परिभाषा लिखिए।
(ii) दो चरों x व y वाले रैखिक समीकरण का मानक रूप लिखिए।
(iii) समान्तर श्रेढ़ी का व्यापक रूप लिखिए।
(iv) द्विघात समीकरण ax² + bx + c= 0 के विविक्तकर ज्ञात करने का सूत्र लिखिए।
(v) क्या (x+1)² = 2(x–3) द्विघात समीकरण है?

उत्तर :

(i) द्रष्टि रेखा : हमारी आंखों से वस्तु को जोड़ने वाली रेखा दृष्टि रेखा कहलाती है|
(ii) A x + B y = C
(iii) a, (a + d ), (a + 2d ), (a + 3d ), ...
(iv) d= b² - 4 a c
(v) हाँ

Q.15: संख्या 12, 15 और 21 का अभाज्य गुणनखण्ड विधि से H.C.F. & L.C.M. ज्ञात कीजिए ।

उत्तर : हल:
12 = 2 × 2 × 3
15 = 5 × 3 
21 = 7 × 3
सार्व गुणनखंड = 3 
HCF = 3  
​LCM = 3 × 2 × 2 × 5 × 7 = 420

Q.16: बिना लंबी विभाजन प्रक्रिया किये बताइये कि परिमेय संख्या 35/50 का दशमलव प्रसार सांत है या अंसात आवर्ती है।

उत्तर : 35/50 => सांत आवर्ती है।
=35/(2^1*5^2)
हम जानते हैं कि प्रत्येक परिमेय संख्या जिसका दशमलव प्रसार सांत है , को p/q के रूप में लिखा जा सकता है
जहाँ p तथा q सह-अभाज्य हैं और q का अभाज्य गुणनखंडन 2^m.5^n के रूप का हैं ।
जहाँ m तथा n ऋणेत्तर पूर्णांक हैं । इसी प्रकार, प्रत्येक परिमेय संख्या , जो p/q के रूप में है , जहां q का रूप ^m.5^n के रूप का नहीं हैं । जहाँ m तथा n ऋणेत्तर पूर्णांक हैं ।

Q.17: किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। p(x) के शून्यकों की संख्या ज्ञात कीजिए।

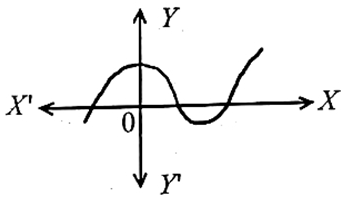
उत्तर : शून्यक की संख्या 3 है, क्योंकि यहाँ पर ग्राफ x-अक्ष को केवल 3 बिन्दुओं पर प्रतिच्छेद करता हैl

Q.18: बिन्दुओं (0, 0) और (36, 15) के बीच की दूरी ज्ञात करो ।

उत्तर :

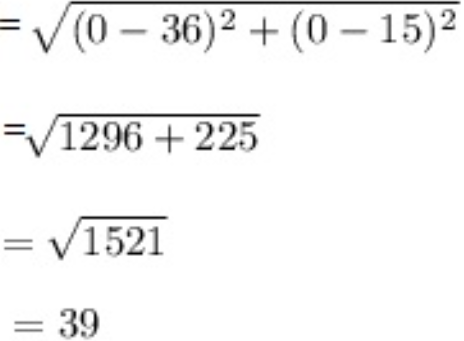
Q.19: 20 बल्बों के एक समूह में 4 बल्ब खराब हैं। इस समूह में से एक बल्ब यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि यह बल्ब खराब है?

उत्तर :

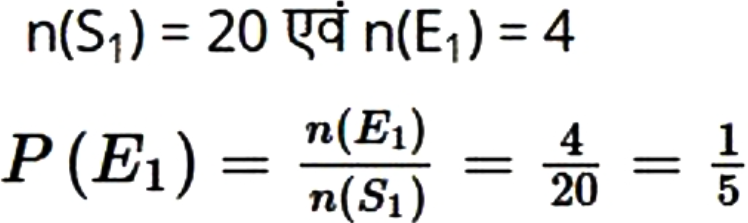
Q.20: एक पाँसे को एक बार फेंका जाता है। एक विषम संख्या प्राप्त करने की प्रायिकता ज्ञात कीजिए।

उत्तर : विषम संख्या :1, 3, 5,
अनुकूल परिणाम की संख्या = 3
अतः, प्रायिकता = अनुकूल परिणाम की संख्या/सभी सम्भव परिणाम की संख्या
= 3/6 = 0.5

Q.21: यदि tan A = cot B, तो सिद्ध कीजिए कि A+ B = 90°.

उत्तर : दिया हुआ है : tan A = cot B

=> tan A = tan (90-B) { हमे मालूम है : cot x = tan (90-x) }

=> A=90-B

=> A+B=90

सिद्ध होता है|

Q.22: बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाईयाँ बराबर होती हैं।

उत्तर :

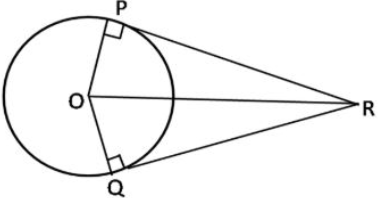
माना कि O केन्द्र वाला एक वृत्त है, माना कि इस वृत्त के बाहर के बिन्दु P है, जिससे वृत पर दो स्पर्श रेखाएँ PQ और PR खींची गई हैं। स्पर्श रेखा PQ वृत के Q बिन्दु को स्पर्श करता है, तथा स्पर्श रेखा PR वृत्त को R बिन्दु पर स्पर्श करता है।

हमें सिद्ध करना है कि , ∠ QPR +∠ ROQ = 180°

अब, Q तथा R को मिलाया गया ।

अत:, QR रेखाखंड है जो कि वृत्त के केन्द्र O पर ∠ POQ बनाता है।

अब चित्र के यह स्पष्ट है कि त्रिज्या OQ ⊥ PQ (स्पर्श रेखा)

∴ ∠ OQP = 90°

उसी तरह, त्रिज्या OR ⊥ PR (स्पर्श रेखा)

∴ ∠ ORP = 90°

अब, चतुर्भुज OQPR में,

आंतरिक कोणों का योग = 360°

⇒ ∠ OQP + ∠ QPR + ∠ PRO + ∠ ROQ = 360°

⇒ 90° + ∠ QPR + 90° + ∠ ROQ = 360°

⇒ 180° + ∠ QPR + ∠ ROQ = 360°

⇒ ∠ QPR + ∠ ROQ = 360° – 180°

⇒ ∠ QPR +∠ ROQ = 180°

अर्थात किसी बाह्य बिन्दु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखंड द्वारा केन्द्र पर अंतरिम कोण का संपूरक होता है।

Q.23: दो वृत्तों की त्रिज्याएँ क्रमशः 19 सेमी. और 9 सेमी. हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है।

उत्तर : पहले वृत्त की परिधि

=2πr=2π×19=38π cm=2πr=2π×19=38π cm

दूसरे वृत्त की परिधि =18π cm=18π cm

या, 2πr=56π2πr=56π

या, 2r=562r=56

या, r=28 cmr=28 cm

प्रश्न के अनुसार, सबसे बड़े वृत्त की परिधि

=38π+18π=56π cm

Q.24: 10 सेमी. त्रिज्या वाले एक वृत्त की कोई जीवा केन्द्र पर एक समकोण अंतरित करती है। संगत लघु वृत्त खण्ड का क्षेत्रफल ज्ञात कीजिए।

उत्तर : लघु वृत्तखंड का क्षेत्रफल

=(1/4) × π r²

= (1/4) × π 10²

=25π sq cm

=78.5398 sq cm

Q.25: सिद्ध कीजिए कि √5 एक अपरिमेय संख्या है।

उत्तर : सबसे पहले इसका उलटा मान लेते हैं; यानि मान लेते हैं कि √5 एक परिमेय संख्या है।
ऐसी संख्या के लिये a और b दो ऐसी संख्या होंगी जहाँ b ≠ 0 तथा a और b प्राइम होंगे, ताकि;
√5= a/b
या, b√5=a

दोनों तरफ का वर्ग करने पर यह समीकरण मिलता है;

5b² = a²
इसका मतलब है कि a², 5 से डिविजिबल होगा और इसलिये a भी 5 से डिविजिबल होगा।
लेकिन यह हमारी पहले के मान का विरोधी है कि a और b कोप्राइम हैं, क्योंकि हमें 5 के रूप में a और b का कम से कम एक कॉमन फैक्टर मिल गया है।
यह हमारे पहले मानी हुई संभावना कि b√5 प्रमेय संख्या है का भी विरोधाभाषी है।

इसलिए एक b√5 अप्रमेय संख्या है सिद्ध हुआ।

Q.26: 135 और 225 का HCF ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए।

उत्तर : मान लीजिए कि 225 = a और 135 = b
यहाँ पर इस समीकरण का प्रयोग करते हैं जिसमें a=bq+r
जहाँ r ≤ 0 < b
तो निम्नलिखित समीकरण मिलता है;
225 = 135 × 1 + 90 जहाँ r = 90 है
अब यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग करने के लिये मान लीजिए कि 135 = a और 90 = b
तो निम्नलिखित समीकरण मिलता है;
135 = 90 × 1 + 45 जहाँ r=45 है
अब यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग करने के लिये मान लीजिए कि 90 = a और 45 = b
तो निम्नलिखित समीकरण मिलता है;
90 = 45 × 2 + 0
यहाँ पर r = 0 मिलता है।
इसलिए HCF = 45

Q.27: द्विघात बहुपद x²–2x–8 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।

उत्तर : x² –2x–8=0
Or, x2–4x+2x–8=0
Or, x(x–4)+2(x–4)=0
Or, (x+2)(x–4)=0
इसलिये शून्यक = -2 और 4
हम जानते हैं कि शून्यक का योग = −b / a या, −2 + 4 = − ( − 2 )
या, LHS = RHS
हम जानते हैं कि शून्यक का गुणनफल = c / a या, −2 x 4 = − 8
शून्यकों के योग और गुणनफल से शून्यकों और गुणांकों के बीच का संबंध सत्यापित हुआ।

Q.28: दो संपूरक कोणों में बड़ा कोण छोटे कोण से 18 डिग्री अधिक है। उन्हें ज्ञात कीजिए।

उत्तर : मान लीजिए कि बड़ा कोण x है और छोटा कोण y है। प्रश्न के अनुसार निम्नलिखित समीकरण मिलते हैं।
x=y+18 और x+y=180°
पहले समीकरण से x का मान दूसरे समीकरण में रखने पर;
x+y=180°
या, y + 18 + y = 180°
या, 2y = 180°−18° = 162°
या, y=81°
पहले समीकरण में y का मान रखने पर;
x = y + 18
या, x = 81° + 18° = 99°
इसलिए, x = 99° और y = 81°

Q.29: किसी A.P. का प्रथम पद 5, अंतिम पद 45 और योग 400 है। पदों की संख्या और सार्व अंतर ज्ञात कीजिए।

उत्तर :
S = n / 2 [2a+(n−1)d]
या, 400=n/2[2×5+(n−1)d]
या, 800=n(5+45)
या, 50 n=800
या, n=16
अब, सार्व अंतर को निम्न तरीके से निकाला जा सकता है;
an=a+(n–1)d
या, 45 = 5 + 15 d
या, 15 d = 40
या, d=40/15=8/3
इसलिए, n=16 और d=8/3

Q.30: 10 और 250 के बीच में 4 के कितने गुणज हैं ?

उत्तर : 10 से बड़ी और 4 से भाज्य होने वाली सबसे छोटी संख्या = 12
जब 250 को 4 से विभाजित किया जाता है तो शेष 2 मिलता है।
इसलिए, इस सीरीज में 4 से विभाजित होने वाली सबसे बड़ी संख्या =250–2=248
अब हमारे पास निम्नलिखित जानकारी है;
पहला टर्म (a) = 12,
अंतिम टर्म (n) = 248
सार्व अंतर(d) = 4
हम जानते हैं, an=a+(n−1)d
या, 248=12+(n–1)4
या, (n–1)4=248–12=236
या, n–1=59
या, n=60
इसलिए, 10 और 250 के बीच 4 से भाज्य संख्याओं का नम्बर = 60

Q.31: एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।

उत्तर : समबाहु त्रिभुज है, तो उसके प्रत्येक शीर्षलंब की लंबाई सामान होगी अतः

समबाहु त्रिभुज के सभी कोण 60 डिग्री के होते हैं

Que : 32. संख्याओं 6 और 20 के अभाज्य गुणनखण्डन विधि से HCF और LCM ज्ञात कीजिए।

उत्तर : 

6 = 2 × 3
20 = 2 × 2 × 5
HCF = 2
LCM = 2 × 2 × 3 × 5 = 60
अब HCF (6, 20) × LCM (6, 20) = 2 × 60 = 120
अत: HCF (6, 20) × LCM (6, 20) = 6 × 20

Que : 33. संख्या 6, 72 और 120 का अभाज्य गुणनखण्डन विधि से H.C.F. ज्ञात कीजिए।

उत्तर :

6 = 2 × 3
72 = 2 × 2 × 2 × 3 × 3
120 = 2 × 2 × 2 × 3 × 5
HCF = 2 × 3 = 6
LCM = 2 × 2 × 2 × 3 × 3 × 5 = 360
अत: अभीष्ट HCF = 6 एवं LCM = 360

Que : 34. बिन्दुओं (2,3) और (4,1) के बीच की दूरियाँ ज्ञात कीजिए।

उत्तर :

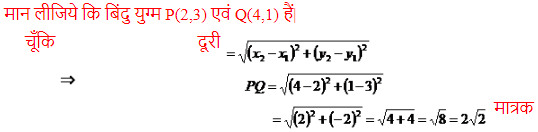
Que : 35. उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (1, – 1), ( – 4, 6) और ( – 3, – 5) है।

उत्तर : शीर्षों A (1,-1), B (-4, 6) और C (- 3, - 5) वाले त्रिभुज ABC का क्षेत्रफल, उपरोक्त सूत्र द्वारा निम्नलिखित है :

Que : 36. दो खिलाड़ी संगीता और रेशमा टेनिस का एक मैच खेलती हैं। संगीता द्वारा मैच जीतने की प्रायिकता 0.62 है। रेशमा के जीतने की क्या प्रायिकता है?

उत्तर : मान लीजिए S और R  क्रमशः संगीता के जीतने और रेशमा के जीतने की घटनाएँ व्यक्त करते हैं।

संगीता के जीतने की प्रायिकता = P(S) = 0.62 (दिया है)

रेशमा के जीतने की प्रायिकता   = P(R) = 1 — P(S)

[चूँकि घटनाएँ R और S पूरक हैं।

= 1 - 0.62 = 0.38

Que : 37. एक बक्से में 3 नीले, 2 सफेद और 4 लाल कंचे (Marbles) है। यदि इस बक्से में से एक कंचा यादृच्छया निकाला गया तो इसकी प्रायिकता है कि यह कंचा (i) सफेद, (ii) नीला, (iii) लाल है।

उत्तर : यह कहना कि कंचा यादृच्छया रूप से निकाला गया है, संक्षिप्त में यह कहने के बराबर है कि सभी परिणाम सम्प्रायिक हैं। अतः,

सभी संभव परिणामों की संख्या = 3 + 2 + 4 = 9      (क्यों?)

मान लीजिए घटनी W 'कंचा सफेद है’ को, घटना B 'कंचा नीला है' को तथा घटना R ‘कंचा लाल है' को व्यक्त करता है।

(i) घटना W के अनुकूल परिणामों की संख्या = 2

Que : 38. निम्नलिखित का मान निकालिए । sin60°.cos30° + sin30°.cos60°

उत्तर : हल :  sin60°.cos30° + sin30°.cos60°

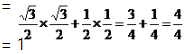
अत: अभीष्ट मान = 1 है।

Que : 39. दर्शाइए कि एक धनात्मक विषम पूर्णांक 4q + 1 या 4g + 3 के रूप का होता है जब q एक पूर्णांक है।

उत्तर : आइए एक धनात्मक विषम पूर्णांक a लेकर, प्रश्न को हल करना प्रारंभ करें। हम a और b = 4 में विभाजन एल्गोरिथ्म का प्रयोग करते हैं।

चूँकि 0 < r < 4 है, इसलिए संभावित शेषफल 0, 1, 2 और 3 हैं।

अर्थात् a संख्याओं 4q,4g + 1, 4q + 2 या 4q + 3 के रूप का हो सकता है जहाँ q भागफल है। चूँकि a एक विषम पूर्णाक है, इसलिए यह 4q और 4q + 2 के रूप का नहीं हो सकता (क्योंकि दोनों 2 से विभाज्य हैं)।

इसलिए, कोई भी धनात्मक विषम पूर्णांक 4q + 1 या 4q +3 के रूप का होगा।

Que : 40. यदि sin A = 3/4 , तो cos A और tan A का मान परिकलित कीजिए।

उत्तर : मान लो DABC एक समकोण D है जिसमें ÐB समकोण है।

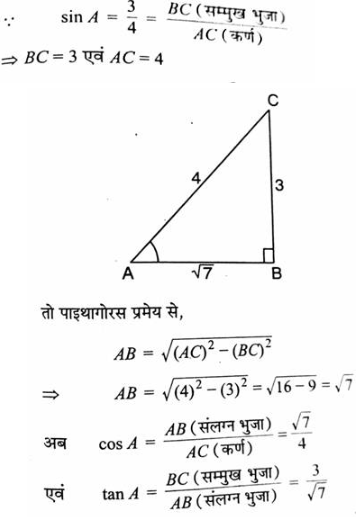
Que: 41. निम्नलिखित का मान निकालिए :

2 tan2 – 45° + cos2 30° – sin2 60°

उत्तर : 

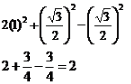
Que : 42. किसी चूड़ी की सहायता से वृत्त खींचिए । वृत्त के बाहर एक बिंदु से वृत्त पर स्पर्श रेखाओं की रचना कीजिए ।

उत्तर : रचना के पद : (1) चूड़ी की सहायता से एक वृत्त खींचा।

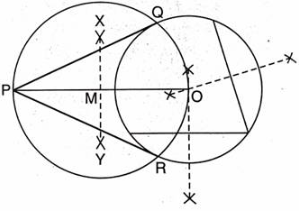
(2) वृत्त का केन्द्र 0 उचित विधि से ज्ञात किया।

(3) वृत्त के बाहर कोई बिन्दु P लिया और OP को मिलाया।

(4) OP का लम्ब-अर्द्धक XY खींचा जो OP को बिन्दु M पर प्रतिच्छेद करता है।

(5) M को केन्द्र लेकर MP = MO की त्रिज्या से एक वृत्त खींचा जो दिए हुए वृत्त को क्रमशः 2 और R बिन्दुओं पर प्रतिच्छेद करता है।

(6) PO और PR को मिलाइए।

अत: PO एवं PR अभीष्ट स्पर्श रेखाएँ हैं। उत्तर

रचना का औचित्य : PO और PR क्रमशः 0Q एवं OR त्रिज्याओं के साथ समकोण बनाती हैं क्योंकि अर्द्धवृत्त के कोण हैं।

Que : 43. एक शंकु के छिन्नक जो 45 cm ऊँचा है, के सिरों की त्रिज्याएँ क्रमशः 28 cm और 7 cm हैं। इसका आयतन ज्ञात कीजिए।

उत्तर : 

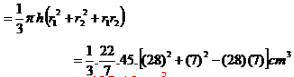
= 485 10cm³

Q.44: 52 पत्तों की अच्छी प्रकार से फेंटी गई एक गड्डी में से एक पत्ता निकाला जाता है। एक फेस कार्ड प्राप्त करने की प्रायिकता ज्ञात कीजिए।

उत्तर : 

 

 

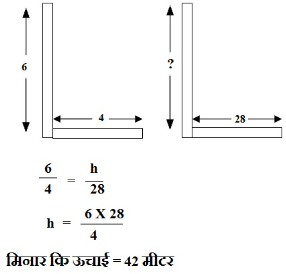
Q.45: लंबाई 6 मीटर वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 मीटर है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 मीटर है। मीनार की ऊँचाई ज्ञात कीजिए।

उत्तर :

MP Board Class 10 Study Material

MP Board Class 10 Study Material
MP Board Class 10 Books	MP Board Class 10 Syllabus
MP Board Class 10 Model Paper