Mathematics Test

Result

Mathematics Test - 44

Score
-
out of -
Rank
-
out of -

TIME Taken - -

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Weekly Quiz Competition

Question 1
1 / -0

Two slits, 4 mm apart, are illuminated by light of wavelength 6000 A. What will be the fringe width on a screen placed 2 m from the slits?

A
0.12 mm

B
0.3 mm

C
3.0 mm

D
4.0 mm

Solution

Fringe width (β) : The separation between any two consecutive bright or dark fringes is called fringe width. In YDSE all fringes are of equal width. Fringe width β = λD/d
Question 2
1 / -0

A coil of inductive reactance $31 Ω$ has a resistance of $8 Ω$ .It is placed in series with a condenser of capacitive reactance $25 Ω$ .The combination is connected to an ac source of 110 V. The power factor of the circuit is :

A
0.33

B
0.56

C
0.64

D
0.80

Solution

$\mathrm{X}_{\mathrm{L}}=31 \Omega, \mathrm{X}_{\mathrm{C}}=25 \Omega, \mathrm{R}=8 \Omega$Impedance of series LCR is$\mathrm{Z}=\sqrt{\left(\mathrm{R}^{2}\right)+\left(\mathrm{X}_{\mathrm{L}}-\mathrm{X}_{\mathrm{C}}\right)^{2}}$$=\sqrt{(8)^{2}+(31-25)^{2}}=\sqrt{64+36}=10 \Omega$Power factor, $\cos \phi=\frac{R}{Z}=\frac{8}{10}=0.8$
Hence, the correct option is (D)
Question 3
1 / -0

In an N-P-N transistor as common emitter amplifier 10¹⁰ electrons enter the emitter in 10^-6 s. If 2% of the electrons are lost in the base. Then Calculate the current transfer ratio and current amplification factor.

A
0.76 ; 38

B
0.98 ; 49

C
1.08 ; 57

D
1.26 ; 68

Solution

Emitter current $I_{e}=\frac{N e}{y}=\frac{10^{10} \times 1.6 \times 10^{-19}}{10^{-6}}=1.6 \mathrm{mABase}$ current $I_{b}=\frac{2}{100} \times 1.6=0.032 \mathrm{mA}$

but $I_{e}=I_{c}+I_{b} \therefore I_{c}=I_{c}=I_{b}=1.6=1.6-0.032=1.568 \mathrm{mA}$

$\therefore \alpha=\frac{I_{c}}{I_{c}}=\frac{1.568}{1.6}=0.98$ and $\beta=\frac{I_{c}}{I_{b}}=\frac{1.568}{0.032}=49$)
Concepts:
Main Concept :Emitter, base and collector terminals of a transistor

A junction transistor consists of a thin piece of one type of semiconductor material between two thicker layers of the opposite type. For example, if the middle layer is p-type, the outside layers must be n-type. Such a transistor is an NPN transistor. One of the outside layers is called the emitter, and the other is known as the collector. The middle layer is the base. The places where the emitter joins the base and the base joins the collector are called junctions.
Manufacturers also make PNP junction transistors. In these devices, the emitter and collector are both a p-type semiconductor material and the base is n-type.
Hence, the correct option is (B)
Question 4
1 / -0

Work done by the system in closed path ABCA, as shown in figure is :

A
Zero

B
(V₁ - V₂) (P₁ - P₂)

C
$\frac{\left(\mathrm{P}_{2}-\mathrm{P}_{1}\right)\left(\mathrm{V}_{2}-\mathrm{V}_{1}\right)}{2}$

D
$\frac{\left(\mathrm{P}_{2} \mathrm{P}_{1}\right)\left(\mathrm{V}_{2}-\mathrm{V}_{1}\right)}{2}$

Solution
Question 5
1 / -0

Estimate the speed of sound in air at standard temperature and pressure. The mass of 1 mole of air is 29.0 × 10^-3 kg.

A
330.94 m s^-1

B
187.6 m s^-1

C
324.5 m s^-1

D
246.2 m s^-1

Solution

At N.T.P., $P=1.013 \times 10^{5} \mathrm{N} \mathrm{m}^{-2}$
volume of air, $V=22400 \mathrm{cm}^{3}=2.24 \times 10^{-2} \mathrm{m}^{3}$
mass of 1 mole of air, $M=29.0 \times 10^{-3} \mathrm{kg}$
Therefore, density of air at N.T.P.
$$
\rho=\frac{M}{V}=\frac{29.0 \times 10^{-3}}{2.24 \times 10^{-2}}=1.295 \mathrm{kg} \mathrm{m}^{-3}
$$
$\mathrm{Now}, v=\sqrt{\frac{\gamma P}{\rho}}=\sqrt{\frac{1.4 \times 1.013 \times 10^{5}}{1.295}}$
$$
=330.94 \mathrm{m} \mathrm{s}^{-1}
$$
Concepts:
Main Concept :
Kinetic Theory of Gases Different equationsKinetic Theory of Gases Different equations used in kinetic theory of gases are listed below.
(i) $\mathrm{pV}=\mathrm{nRT}=\frac{\mathrm{m}}{\mathrm{M}} \mathrm{RT}$
$(\mathrm{m}=$ mass of gas in gms)
(ii) Density $\rho=\frac{\mathrm{m}}{\mathrm{V}}$
(general)
$=\frac{p M}{R T}$
(for ideal gas)Kinetic Theory of Gases Different equations used in kinetic
theory of gases are listed below.
(i) $\mathrm{pV}=\mathrm{nRT}=\frac{\mathrm{m}}{\mathrm{M}} \mathrm{RT} \quad(\mathrm{m}=$ mass of gas in gms $)$
(ii) Density $\rho=\frac{\mathrm{m}}{\mathrm{V}}$
(general)
$=\frac{\mathrm{pM}}{\mathrm{RT}}$
(for ideal gas)
Hence, the correct option is (A)
Question 6
1 / -0

Prism angle & refractive index for a prism are 60^o & 1.414. Angle of minimum deviation will be :

A
15^o

B
30^o

C
45^o

D
60^o

Solution

$\mu=\frac{\sin \frac{\left(\Lambda+\delta_{\mathrm{m}}\right)}{2}}{\sin 30^{\circ}}$
$\Rightarrow 1.414=\frac{\sin \frac{\left(60+\delta_{\mathrm{m}}\right)}{2}}{\sin 30^{\circ}}$
$\Rightarrow \quad \sin \left(\frac{60^{\circ}+\delta_{\mathrm{m}}}{2}\right)=0.707=\sin 45^{\circ}$
$\Rightarrow \quad \frac{60+\delta_{\mathrm{m}}}{2}=45^{\circ} \Rightarrow \delta_{\mathrm{m}}=30^{\circ}$
Hence, the correct option is (B)
Question 7
1 / -0

An electron gun G emits electron of energy 2 kev travelling in the (+)ve x-direction. The electron are required to hit the spot S where GS = 0.1m & the line GS makes an angle of $60^{0}$ with the x-axis, as shown in the fig. A uniform magnetic field $\underset{B}{\to}$ parallel to GS exists in the region outsides to electron gun. Find the minimum value of B needed to make the electron hit S.

A

B

C

D

Solution
Question 8
1 / -0

A body executes S.H.M. of period 20 seconds. Its velocity is 5 cm s^-1, 2 seconds after it has passed the mean position. Find amplitude of the bob :

A
21.45 cm

B
16.56 cm

C
19.67 cm

D
15.34 cm

Solution

Here, $T=20 \mathrm{s}$
Also, when $\mathrm{t}=2 \mathrm{s}, \mathrm{v}=5 \mathrm{cm} \mathrm{s}^{-1}$
Now, $\mathrm{v}=\mathrm{r} \omega \cos \omega \mathrm{t}=\mathrm{r} \times \frac{2 \pi}{\mathrm{T}} \cos \frac{2 \pi}{\mathrm{T}} \mathrm{t}$
$\therefore \quad 5=\mathrm{r} \times \frac{2 \pi}{20} \cos \frac{2 \pi}{20} \times 2$ or $\frac{\mathrm{r} \pi}{10} \cos \frac{\pi}{5}=5$
or $\frac{\pi \mathrm{r}}{10} \cos 36^{\circ}=5$ or $\frac{\pi \mathrm{r}}{10} \times 0.8090=5$
or $\mathrm{r}=19.67 \mathrm{cm}$
Concepts:
Main Concept:
General equation of SHM The necessary and sufficient condition for SHM is $F=-k x$
we can write above equation in the following way:
$\mathrm{ma}=-\mathrm{kx}$
$m \frac{d^{2} x}{d t^{2}}=-k x$
$\frac{d^{2} x}{d t^{2}}+\frac{k}{m} x=0$
Equation (1) is Double Differential Equation of SHM.
Now $\frac{d^{2} x}{d t^{2}}+\omega^{2} x=0$
It's solution is $\mathbf{x}=\mathbf{A} \sin (\omega t+\phi)$
where $\omega=$ angular frequency $=\sqrt{\frac{k}{m}}$
$\mathrm{x}=$ displacement from mean position
$\mathrm{k}=\mathrm{SHM}$ constant.
The equality $(\omega t+\phi)$ is called the phase angle or simply the phase of the SHM and $\phi$ is the initial phase i.e., the phase at $t=0$ and depends on initial position and direction of velocity at $t=0$.
Hence, the correct option is (C)
Question 9
1 / -0

A uniform rod of mass m and length ℓ is rotating with constant angular velocity ω about an axis which passes through its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is Y. Neglect gravity. The strain at the mid point of the rod is :

A
$\mathrm{m} \omega^{2} \mathrm{Y} / 8 \mathrm{AY}$

B
$\frac{3 m \omega^{2} \ell}{8 A Y}$

C
$\frac{3 m \omega^{2} \ell}{4 A Y}$

D
$\frac{m \omega^{2} \ell}{4 A Y}$

Solution

Young's Modulus of Elasticity $\mathbf{Y}=\frac{\overline{\mathrm{F}} / \mathbf{A}}{\Delta \ell / \ell}=\frac{\mathrm{F} \ell}{\mathrm{A} \Delta \ell}$
$\mathbf{F}=\mathbf{m g}$ and $\mathbf{A}=\pi \mathbf{r}^{2}$
It is defined as the ratio of the normal stress to the longitudinal strain.
Concepts:
Main Concept:
Young's Modulus of Elasticity
Young's Modulus of Elasticity $\mathrm{Y}=\frac{\text { F/A }}{\Delta \ell / \ell}=\frac{\mathrm{F} \ell}{\mathrm{A} \Delta \ell}$
$\mathbf{F}=\mathbf{m g}$ and $\mathbf{A}=\pi \mathbf{r}^{2}$
It is defined as the ratio of the normal stress to the longitudinal strain.
Hence, the correct option is (B)
Question 10
1 / -0

Two masses m₁ and m₂ are connected by a string of length l. They are held in a horizontal plane at a height H above two heavy plates A and B made of different material placed on the floor. Initially distance between two masses is a < l. When the masses are released under gravity they make collision with A and B co - efficient of restitution 0.8 and 0.4 respectively. The time after the collision when the string becomes tight is :

A
$\frac{5}{2} \sqrt{\frac{l^{2}-a^{2}}{2 g H}}$

B
$\sqrt{\frac{2 \mathrm{g}}{\mathrm{H}}}$

C
$\frac{3}{2} \sqrt{\frac{l^{2}-a^{2}}{2 g H}}$

D
None of these

Solution

Elastic and Inelastic CollisionsA perfectly elastic collision is defined as one in which there is no loss of kinetic energy in the collision. An inelastic collision is one in which part of the kinetic energy is changed to some other form of energy in the collision. Any macroscopic collision between objects will convert some of the kinetic energy into internal energy and other forms of energy, so no large scale impacts are perfectly elastic. Momentum is conserved in inelastic collisions, but one cannot track the kinetic energy through the collision since some of it is converted to other forms of energy. Collisions in ideal gases approach perfectly elastic collisions, as do scattering interactions of sub-atomic particles which are deflected by the electromagnetic force. Some large-scale interactions like the slingshot type gravitational interactions between satellites and planets are perfectly elastic.

Collisions between hard spheres may be nearly elastic, so it is useful to calculate the limiting case of an elastic collision. The assumption of conservation of momentum as well as the conservation of kinetic energy makes possible the calculation of the final velocities in two-body collisions.

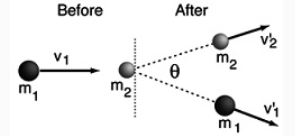
An elastic collision is defined as one in which both conservation of momentum and conservation of kinetic energy are observed. This implies that there is no dissipative force acting during the collision and that all of the kinetic energy of the objects before the collision is still in the form of kinetic energy afterward.
For macroscopic objects which come into contact in a collision, there is always some dissipation and they are never perfectly elastic. Collisions between hard steel balls as in the swinging balls apparatus are nearly elastic.
"Collisions" in which the objects do not touch each other, such as Rutherford scattering or the slingshot orbit of a satellite off a planet, are elastic collisions. In atomic or nuclear scattering, the collisions are typically elastic because the repulsive Coulomb force keeps the particles out of contact with each other.
Collisions in ideal gases are very nearly elastic, and this fact is used in the development of the expressions for gas pressure in a container.

Coefficient of restitution
The coefficient of restitution (COR) is a measure of the "bounciness" of a collision between two objects: how much of the kinetic energy remains for the objects to rebound from one another vs. how much is lost as heat, or work done deforming the objects.
The coefficient, e is defined as the ratio of relative speeds after and before an impact, taken along the line of the impact:
Coefficient of restitution(e) = Relative speed after collision/Relative speed before collision

Hence, the correct option is (A)