Let us use J, K, L, M and N as codes for Jack, Kiara, Liam, Mike and Nico respectively.
Using statements 2, 4 and 6, we can have the following table to start with:
Statement 2 gives that the person sitting in second position copied his third answer from the person before him. Hence person sitting in the first position must answer B for question 3.
Statement 6 mentions that the person sitting in the middle did not copy his answer.Since he answered C for question 2. The person sitting in front must not have answered C for question 2. Hence the person in position 2 for question can answer either A/B.
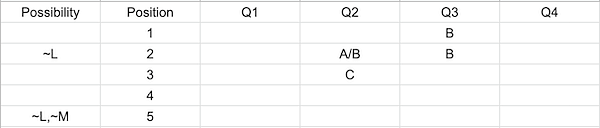
Given J sits one place in front of L. Since L cannot sit at position 2 and 5 . J can sit only at 2,3. If J sits at 2 or 3 L must sit at 3 or 4.
Given in statement 4 M does not not sit position 5 nor answer option B for question 3. Hence he can only sit at either 3 or 4.
If J sits at 3 and L sits at 4 M does not have a place to sit. Hence J must sit at 2, L at 3 and M at 4.
Also, statement 3 says that J marked C twice and hence A and B were marked exactly once by him. Hence C must be answered for Q1 and Q4.
Statement 1 says that B was marked twice in question 1 hence it must be answered for by L and M because the person sitting at first and final position cannot answer B and person at position has already answered Q1 with C hence B must be answered for Q1 by persons L and M and since they are consecutively seated they must have copied. After placing as per the mentioned conditions the table looks like this :
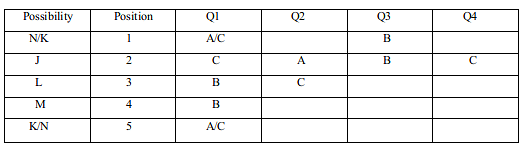
Since the a set of persons must copy only one answer. The person sitting at position 1 cannot place C for Q1 because if he does that then there will be two copied answers between 1st and 2nd seated people. Hence he must answer A for question 1.
Note that in statement 3 it is mentioned that Nico marked the answer as option C only for Q1. Hence Nico is at position 5 and Kiara at position 1.
Also, exactly 2 persons marked B as answers to Q1. So,
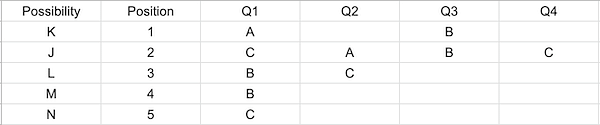
Now, we have copied answers for pairs (3,4) and (1,2) and for questions 1 and 3.
So, pairs (2,3) and (4,5) must have copied answers for Q2 and Q4.
And since pair (2,3) did not copy answer for Q2, they must have done it for Q4. And the pair (4,5) must have copied for Q2.
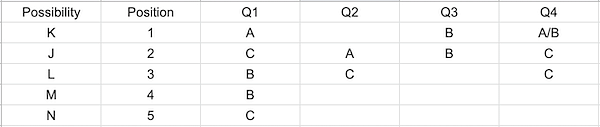
Statement 4 tells that person sitting at the last position answers B for question 2. Since (4,5) copied Q2 person at position 4 must answer B for Q4
Now since, each of the 5 person must have at least one A, B and C each as the answers. We further deduce the following:
For M one of Q3 and Q4 must be answered with A and C. Since Q4 cannot be answered C by M as it would mean that he had copied this from L this is a false case. Hence he answers A for Q3 and C for Q4.
For L since we must have at least one answer to be A we must Q3 with A.
For K we must have at least 1 answer to be C and we cannot answer Q4 with C we must answer Q2 with C.
The remaining Q4 for K can be answered with A/B but not C because J has answered Q4 with C.
The last person can answer Q3 with A/B because A/B because C cannot be placed as M answered Q3 with C similarly for Q4 only B/C can be used.
Also, the last person marked B as the answer for Q2. So
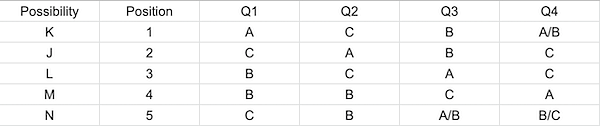
Now, Nico only answered C for Q1. If he answers B for Q3 . He cannot answer A for any of the Questions hence he must answer Q3 with option A. Since he only answers one question with option C he must answer Q4 with B.
The final table looks like :
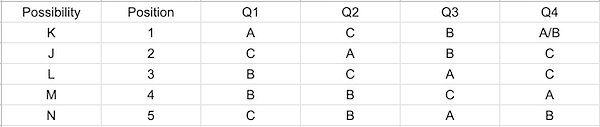
Since Kiara is the first person among the 5 friends, she did not copy any answer from her friends.


 Get latest Exam Updates
Get latest Exam Updates 
 ×
×
















