Let us start by tabulating the data available.
We have no information about the number of persons in each club.
The sports-sports cell in the table represents the number of persons from sports club who stayed in sports club. Since we do not have this information (we have information only regarding the movement from one club to another), let us mark all such cells with X.
The cell sports-dramatics (row-column) represents the number of students from sports club who left for dramatics club. Therefore, the cell sports-total will provide the number of students who left the sports club and the cell total-sports will provide the number of students who left other clubs for the sports club.
The number of persons who moved from dramatics club to the sports club is the same as the number of persons who moved from the sports club to the dramatics club. The same is the case with sports club and literary club as well. Let us use ‘a’ to denote the number of persons who moved from the dramatics club to the sports club and ‘b’ to denote the number of persons who moved from sports club to literary club. The number of persons who moved out of sports and quiz clubs is the same. Let us denote it by ‘c’.
A total of 21 students left one club for another. No person moved from the quiz club to sports club (quiz-sports = 0).
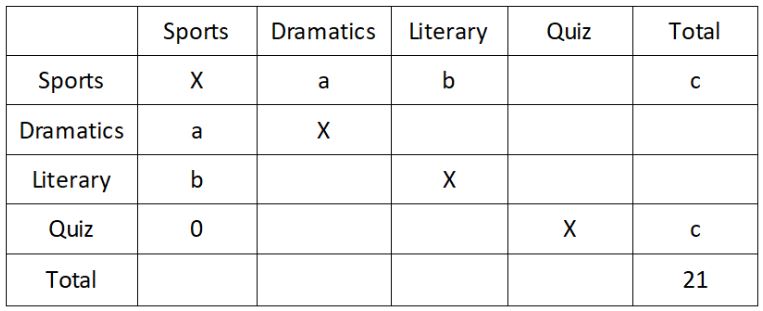
The number of persons who moved to the literary club is one more than the number of persons who moved to the sports club. Let the number of persons who moved to the literary club be ‘d+1’ and the number of persons who moved to the sports club be ‘d’.
The number of persons who left the quiz club for the dramatics club and the literary club is the same. Let us denote the number of persons who left the quiz club for dramatics club by ‘e’. 4 students moved out of dramatics club and 5 students moved out of literary club.
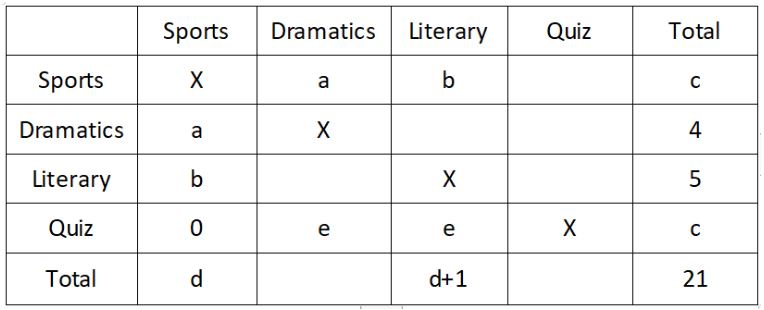
As we can see from the table, c+c+4+5 =21
⇒ c = 6
The number of students who left other clubs for dramatics club is 4 more than the number of students who left other clubs for the quiz club.
Let the number of students who left other clubs for quiz club be ‘f’.
⇒ Number of students who left other clubs for dramatics club = f + 4.
The number of students who joined sports club is exactly half the number of students who left it. We know that 6 students left the sports club. Therefore, 3 students should have joined the sports club. ⇒ d = 3
We can see from the table that e + e = 6
⇒ e = 3
Let us fill the vacant cells with variables from g to k. We get the following table.
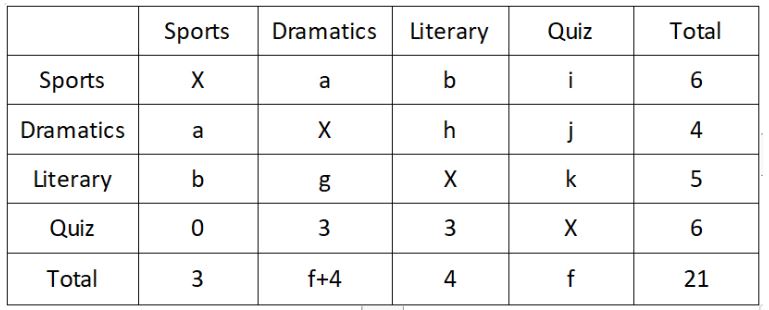
f + f + 4 + 3 + 4 = 21
⇒ 2f = 10
f = 5
a+b = 3
a+b+i = 6
⇒ i = 3
a+h+j = 4 --------------(1)
b+h = 1 ----------------(2)
a+b = 3 ----------------(3)
b+g+k = 5 -------------(4)
j + k = 2 --------------(5)
a+g = 6 ---------------(6)
Let us rewrite every variable in terms of 'a'.
b = 3-a
g =6-a
Substituting these values in (4), we get,
3-a+6-a+k = 5
9-2a+k = 5
k = 2a-4
Substituting the value of 'k' in (5), we get,
j+2a-4 = 2
j = 6-2a
(1)⇒ a+h+j = 4
a + h + 6 - 2a = 4
⇒ h = a - 2
It has been given that at least one student moved from Sports to Literary club. Therefore, the value of 'a' cannot be 3.
We know that k=2a-4. Therefore, the value of 'a' should be at least 2.
2 is the only value that falls within the range.
Solving the equations using a=2, we get the following table:
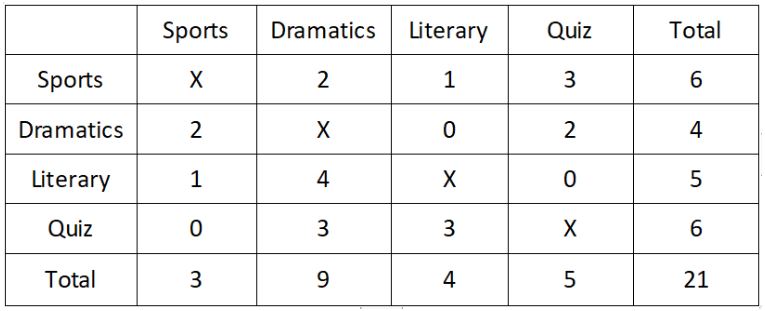
Maximum number of people left literary club for dramatics club. Therefore, option A is the right answer.


 Get latest Exam Updates
Get latest Exam Updates 
 ×
×
















