Some Applications of Trigonometry test

Result

Some Applications of Trigonometry test - 36

Score
-
out of -
Rank
-
out of -

TIME Taken - -

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Weekly Quiz Competition

Question 1
1 / -0

A man on the top of a rock observed a boat coming towards the rock with a uniform speed. It takes $$15$$ minutes for the angle of depression to change from $$\displaystyle 60^{\circ}$$ to $$\displaystyle 30^{\circ}$$ then what time will the boat take to reach the shore?

A
$$5$$ mintues

B
$$10$$ mintues

C
$$\displaystyle 7\frac{1}{2}$$ mintues

D
$$\displaystyle 2\frac{1}{2}$$ mintues

Solution

Let, the Height of the Rock be $$h$$
so, $$tan30^o=\dfrac{h}{BD}\Rightarrow BD=h\sqrt3 \\tan60^o=\dfrac {h}{BC}\Rightarrow BC=\dfrac{h}{\sqrt3}$$

Now, Distance travelled by Boat in 15 minutes $$=h\sqrt3-\dfrac{h}{\sqrt3}$$

$$\Rightarrow v=\dfrac{h\sqrt3-\dfrac{h}{\sqrt3}}{15}\Rightarrow v=\dfrac{2h}{15\sqrt3}$$

Now to reach the Shore it has to travel Distance $$\dfrac{h}{\sqrt3}$$ in Time $$t$$

$$\Rightarrow t=\dfrac{\dfrac{h}{\sqrt3}}{\dfrac{2h}{15\sqrt3}}=7\dfrac12 \ minutes$$
Question 2
1 / -0

The height of a tower is $$100 \sqrt3$$. The angle of elevation of its top from a point $$100 m$$ away from its foot(base) is ______.

A
30$$^o$$

B
45$$^o$$

C
60$$^o$$

D
90$$^o$$

Solution

$$AB =$$ tower, $$O$$ is the point of observation.

Given that height of the tower is $$100$$$$\sqrt3$$

$$\therefore$$ $$AB = 100$$$$\sqrt3$$, $$OA = 100\ m$$

$$\therefore$$ $$\tan$$ $$\theta$$ = $$\displaystyle{\frac{AB}{OA} = \frac{100\sqrt3}{100}}$$ $$=$$ $$\sqrt3$$

$$\therefore \theta$$ $$= 60$$ $$^o$$

$$\therefore$$ Angle of elevation is $$60^o$$.

So, option C is correct.
Question 3
1 / -0

If the given object is above the level of the observer, then the angle by which the observer raises his head is called _____.

A
Angle of depression

B
Angle of elevation

C
Line of sight

D
Horizontal level

Solution

If the given object is above the level of the observer, then the angle by which the observer raises his head is called angle of elevation.
Question 4
1 / -0

In case of angle of depression the observer has to look _____ to view the object.

A
Straight

B
Anywhere

C
Down

D
Up

Solution

In case of angle of depression, the observer has to look down to view the object.
Question 5
1 / -0

From a point at a height $$h$$ m above a lake, the angle of elevation of a cloud is $$\displaystyle \alpha $$ and the angle of depression of its reflection in the lake is $$\displaystyle \beta $$. The height of the cloud above the surface of the lake is

A
$$\displaystyle \frac{h \cos\left ( \alpha +\beta \right ) }{\cos \left ( \alpha -\beta \right )}m$$

B
$$\displaystyle \frac{h \sin \left ( \alpha +\beta \right ) }{\cos \left ( \alpha -\beta \right )}m$$

C
$$\displaystyle \frac{h \sin \left ( \alpha -\beta \right ) }{\cos \left ( \alpha +\beta \right )}m$$

D
$$\displaystyle \frac{h \sin \left ( \alpha +\beta \right ) }{\sin \left (\beta -\alpha \right )}m$$

Solution

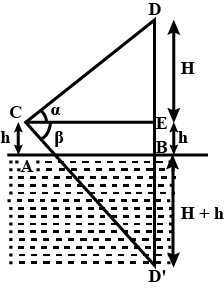
Let $$H$$ be the height of the cloud from the point above $$h\text{ m}$$ from the lake surface.
Now the distance of the reflection from the lake surface be $$H+h \text{ m}$$
Now, In $$\triangle CDE,$$
$$\Rightarrow \tan { \alpha } =\dfrac { DE }{ CE } $$
$$\Rightarrow CE=\dfrac { DE }{ \tan { \alpha } } =\dfrac { H }{ \tan { \alpha } } \longrightarrow \left( 1 \right) $$
In $$\triangle CED',$$
$$\Rightarrow \tan { \beta } =\dfrac { ED' }{ CE } $$
$$\Rightarrow CE=\dfrac { ED' }{ \tan { \beta } } =\dfrac { H+2h }{ \tan { \beta } } \longrightarrow \left( 2 \right) $$
From equation $$ \left( 1 \right)\;\&\; \left( 2 \right),$$ we get
$$\Rightarrow \dfrac { H }{ \tan { \alpha } } =\dfrac { H+2h }{ \tan { \beta } } $$
$$\Rightarrow H\tan { \beta } =H\tan { \alpha } +2h\tan { \alpha } $$
$$\Rightarrow H\left( \tan { \beta } -\tan { \alpha } \right) =2h\tan { \alpha } $$
$$\Rightarrow H=\dfrac { 2h\tan { \alpha } }{ \tan { \beta } -\tan { \alpha } } $$
Now, height of the cloud above the lake surface
$$\Rightarrow H+h=\dfrac { 2h\tan { \alpha } }{ \tan { \beta } -\tan { \alpha } } +h$$
                   $$=\dfrac { 2h\tan { \alpha } +h\tan { \beta } -h\tan { \alpha } }{ \tan { \beta } -\tan { \alpha } } $$
                   $$=\dfrac { h\left( \tan { \alpha } +\tan { \beta } \right) }{ \tan { \beta } -\tan { \alpha } } $$
                   $$=h\left[ \dfrac { \dfrac { \sin { \alpha } }{ \cos { \alpha } } +\dfrac { \sin { \beta } }{ \cos { \beta } } }{ \dfrac { \sin { \beta } }{ \cos { \beta } } -\dfrac { \sin { \alpha } }{ \cos { \alpha } } } \right] $$
                   $$=h\left[ \dfrac { \dfrac { \sin { \alpha } \cos { \beta } +\cos { \alpha } \sin { \beta } }{ \cos { \alpha \cos { \beta } } } }{ \dfrac { \sin { \beta } \cos { \alpha } -\cos { \beta } \sin { \alpha } }{ \cos { \alpha \cos { \beta } } } } \right] $$
Hence, the answer is $$h\left[ \dfrac { \dfrac { \sin { \alpha } \cos { \beta } +\cos { \alpha } \sin { \beta } }{ \cos { \alpha \cos { \beta } } } }{ \dfrac { \sin { \beta } \cos { \alpha } -\cos { \beta } \sin { \alpha } }{ \cos { \alpha \cos { \beta } } } } \right]$$  $$=\displaystyle \frac{h \sin \left ( \alpha +\beta \right ) }{\sin \left (\beta -\alpha \right )}m$$
Question 6
1 / -0

The angles of depression of the top and the bottom of a $$10\ m$$ tall building observed from the top of a tower are $$\displaystyle 30^{0} $$ and $$\displaystyle 45^{0}$$ respectively. Find the height of the tower (in $$m$$)

A
$$\displaystyle 20+5\sqrt{2}$$

B
$$\displaystyle 12+10\sqrt{2}$$

C
$$\displaystyle 15+5\sqrt{3}$$

D
$$\displaystyle 18+3\sqrt{3}$$

Solution

Let the height of the tower be $$H$$

we can see that, $$BCDE$$ is a rectangle
so, $$BE=CD=10\\ \&\ BC=DE$$

Also, we can see that, $$H=AC+CD\Rightarrow H=AC+10\Rightarrow AC=H-10$$

Now, in $$\triangle ADE$$
$$\tan45^o=\dfrac{AD}{DE}\Rightarrow 1=\dfrac{AD}{DE}\Rightarrow AD=DE\Rightarrow DE=H\\ $$

$$\therefore BC=DE=H $$

Now, in $$\triangle ABC$$
$$\tan30^o=\dfrac{AC}{BC}\Rightarrow \dfrac{1}{\sqrt3}=\dfrac{H-10}{H}\Rightarrow H=\sqrt3H-10\sqrt3\Rightarrow 10\sqrt3=(\sqrt3-1)H\\ \Rightarrow H=\dfrac{10\sqrt3}{\sqrt3-1}=\dfrac{10\sqrt3*(\sqrt3+1)}{(\sqrt3-1)(\sqrt3+1)}=5\sqrt3(\sqrt3+1)=15+5\sqrt3$$

Therefore, Answer is $$15+5\sqrt3$$
Question 7
1 / -0

From the foot of a tower, the angle of elevation of the top of a column is 60$$^{\circ}$$ and from the top of the tower the angle of elevation is 30$$^{\circ}$$. If the height of the tower is 25 m, the height of the column is _____

A
$$25$$ m

B
$$12.5$$ m

C
$$37.5$$ m

D
$$47.5$$ m

Solution

Let $$AB$$ be the tower and $$CD$$ be the column.
Then $$AB = 25$$ m. $$\angle EBD = 30^{\circ}$$ and $$\angle CAD = 60^{\circ}$$
$$CE = AB = 25$$ m,
Let $$ED = x$$ m

$$ \cot 30^{\circ}$$ = $$\frac{BE}{ED} $$

$$ \dfrac{BE}{x} = \sqrt{3} $$

$$BE = \sqrt{3 }x$$

Also, $$\cot 60^{\circ}$$ = $$\dfrac{AE}{CD}$$
$$ \dfrac{AC}{25 + x} = \dfrac{1}{\sqrt{3}} $$
$$AC = \dfrac{25 + x}{\sqrt3}$$

Now, $$BE = AC$$

$$\therefore$$ $$\sqrt3$$x = $$\displaystyle{\frac{25 + x}{\sqrt3}}$$
$$ 3x = 25 + x $$
$$2x = 25$$
$$x = 12.5\ \text{m}$$
$$\therefore$$ Height of the column $$= (25 + 12.5)\ \text{m} = 37.5\ \text{m}$$

So, option C is correct.
Question 8
1 / -0

An observer $$1.5$$ m tall is $$28.5$$ m away from a tower and the angle of elevation from the eye of the observer is $$45^o$$. The height of the tower is:

A
$$27$$ m

B
$$30$$ m

C
$$28.5$$ m

D
None of these

Solution

Let $$AB$$ be the observer and $$CD$$ be the tower also refer the given figure :
$$AC = BE = 28.5 m$$
$$AB$$ =$$CE$$ =$$1.5$$ m,
Let $$DE$$=$$ h$$ m

$$\therefore$$ From right angled $$\triangle BED$$,
tan 45$$^o=\displaystyle{\frac{DE}{BE} \Rightarrow 1 = \frac{h}{28.5}}$$
$$h = 28.5 $$
$$\therefore$$ Height of tower $$CD
$$= h + 1.5$$
$$= 28.5 + 1.5$$
$$= 30\ m$$
Question 9
1 / -0

The heights of the two poles are $$80$$ m and $$65$$ m. If the line joining their tops makes an angle of 45$$^o$$ with the horizontal line passing through their top, then the distance between the poles is ______.

A
$$22.5$$ m

B
$$15$$ m

C
$$30$$ m

D
$$7.5$$ m

Solution

Refer the figure:
Let AB and CD be the poles of height 80 m and 65 m respectively.
Draw, DE $$\perp$$ AB then, $$\angle EDB = 45^o$$

Now, $$EB = (AB - AE) = (80 - 65)$$m = $$15$$m.

$$\therefore$$ cot 45$$^o$$ = $$\displaystyle{\frac{ED}{EB} \Rightarrow 1 = \frac{ED}{15} \Rightarrow ED = 15 m}$$

$$\therefore AC = ED = 15$$ m.

So, option B is correct.
Question 10
1 / -0

The angle of elevation of the top of a tower from a point on the ground $$30$$ m away fro the foot of the tower is 30$$^o$$. The height of the tower is _____.

A
$$30$$ m

B
$$10$$$$\sqrt3$$ m

C
$$10$$ m

D
$$10$$ $$\sqrt2$$ m

Solution

AB = height of tower $$= h, \theta = 30^o, OA = 30$$ m
$$\therefore$$$$\displaystyle{\frac{AB}{OA}}$$ = tan$$\theta$$ $$\Rightarrow$$ $$\displaystyle{\frac{1}{\sqrt3} = \frac{h}{30}}$$ $$\Rightarrow$$ h = 10$$\sqrt3$$
$$\therefore$$ Height of the tower is 10$$\sqrt3$$ m.

So, option B is correct.