Wave Optics Test

Result

Wave Optics Test - 72

Score
-
out of -
Rank
-
out of -

TIME Taken - -

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Weekly Quiz Competition

Question 1
1 / -0

Let a beam of wavelength $$\lambda$$ fall on parallel reflecting planes with separation $$d$$, then the angle $$\theta$$ that the beam should make with the planes so that reflected beams from successive planes may interfere constructive should be (where, $$n = 1, 2, ....)$$.

A
$$\cos^{-1}\left (\dfrac {n\lambda}{2d}\right )$$

B
$$\sin^{-1}\left (\dfrac {n\lambda}{2d}\right )$$

C
$$\sin^{-1}\left (\dfrac {n\lambda}{d}\right )$$

D
$$\tan^{-1}\left (\dfrac {n\lambda}{d}\right )$$

Solution

From the adjoining figure path difference between the beams reflected from successive planes
$$= AM + AN = 2d\sin \theta$$
For constructive interference
$$2d\sin \theta = n\lambda$$
$$\sin \theta = \dfrac {n\lambda}{2d}$$
$$\theta = \sin^{-1} \left (\dfrac {n\lambda}{2d}\right )$$.
Question 2
1 / -0

Two coherent poiunt sources of frequency $$(f=\dfrac {10v}{d}$$ where $$v$$ is speed of light) are placed at a distance $$d$$ apart as shown in figure. The receiver is free to move along the dotted line shown in the figure. Find the total number of maxima observed by the receiver.

A
$$6$$

B
$$7$$

C
$$5$$

D
$$8$$

Solution
Question 3
1 / -0

In Young's double slit experiment, one of the slit is wider than another, so that amplitude of the light from one slit is double of that from other slit. If $$I_m$$ be the maximum intensity, the resultant intensity I when they interfere at phase difference $$\phi$$ is given by.

A
$$\displaystyle\frac{I_m}{9}(4+5\cos\phi)$$

B
$$\displaystyle\frac{I_m}{3}\left(\displaystyle 1+2\cos^2\frac{\phi}{2}\right)$$

C
$$\displaystyle\frac{I_m}{5}\left(\displaystyle 1+4\cos^2\frac{\phi}{2}\right)$$

D
$$\displaystyle\frac{I_m}{9}\left(\displaystyle 1+8\cos^2\frac{\phi}{2}\right)$$

Solution

Given, $$a_1=2a_2$$

$$I_1=4I', I_2=I'$$

We know that, $$I_m=(\sqrt{I_1}+\sqrt{I_2})^2$$

$$=(\sqrt{4I'}+\sqrt{I'})^2=9I'$$

$$\therefore I=I_1+I_2+2\sqrt{I_1I_2}\cos\phi$$

$$=4I'+I'+2\sqrt{4I'\cdot I'}\cos\phi$$

$$=4I'+I'+4I'\cos\phi$$

$$=5I'+4I'\cos\phi$$

$$=I'(5+4\cos\phi)$$

$$=\displaystyle\frac{I_m}{9}\left[5+4(2\cos^2\displaystyle\frac{\phi}{2}-1\right]$$

$$=\displaystyle\frac{I_m}{9}\left[5+8\cos^2\displaystyle\frac{\phi}{2}-4\right]$$

$$=\displaystyle\frac{I_m}{9}\left[1+8\cos^2\frac{\phi}{2}\right]$$.
Question 4
1 / -0

Light of wavelength $$\lambda$$ is incident on slit of width $$d$$. The resulting diffraction pattern is observed on a screen placed at distance $$D$$. The linear width of central maximum is equal to width of the slit, then $$D=$$ _________

A
$$\cfrac { { d }^{ 2 } }{ 2\lambda } $$

B
$$\cfrac { { 2\lambda }^{ 2 } }{ d } $$

C
$$\cfrac { d }{ \lambda } $$

D
$$\cfrac { 2\lambda }{ d } $$

Solution

Position of first minima above the central maxima $$y = \dfrac{\lambda D}{d}$$
So, linear width of the central maxima $$ = 2y = \dfrac{2\lambda D}{d}$$
Given : $$2y = d$$
where $$d$$ is the width of slit.
$$\therefore$$ $$\dfrac{2\lambda D}{d} = d$$
$$\implies \ D = \dfrac{d^2}{2\lambda}$$
Question 5
1 / -0

A stationary sound source 's' of frequency 334 Hz and a stationary observer 'O' are placed near a reflecting surface moving away from the source with velocity 2 m/sec as shown in the figure. If the velocity of the sound waved is air is V= 330 m/sec, the apparent frequency of the echo is

A
332 Hz

B
326 Hz

C
334 Hz

D
330 Hz

Solution
Question 6
1 / -0

A vessel $$ABCD$$ of $$10\ cm$$ width has two small slits $$S_{1}$$ and $$S_{2}$$ sealed with identical glass plates of equal thickness. The distance between the slits is $$0.8\ mm$$. $$POQ$$ is the line perpendicular to the plane $$AB$$ and passing through $$O$$, the middle point of $$S_{1}$$ and $$S_{2}$$. A monochromatic light source is kept at $$S, 40\ cm$$ below $$P$$ and $$2m$$ from the vessel, to illuminate the slits as shown in the figure below. Calculate the position of the central bright fringe on the other wall $$CD$$ with respect to the line $$OQ$$. Now, a liquid is poured into the vessel and filled up to $$OQ$$. The central bright fringe is found to be at $$Q$$. Calculate the refractive index of the liquid.

A
(a) $$y = 2\ cm$$. (b) $$\mu = 1.0016$$.

B
(a) $$y = 2\ cm$$. (b) $$\mu = 2.0016$$.

C
(a) $$y = 12\ cm$$. (b) $$\mu = 1.0016$$.

D
(a) $$y = 2\ cm$$. (b) $$\mu = 13.0016$$.

Solution
Question 7
1 / -0

In a biprism experiment, interference patterns are obtained on a screen kept at a distance of $$1.5\ m$$ from the slit. A convex lens is interposed between the slit and the eye-piece which gives two images of slit $$0.8\ cm$$ apart. The distance of the convex lens from the slit is $$40\ cm$$. The width of $$20$$ fringes, if the wavelength of the light used is $$5270 \mathring{A}$$ will be

A
$$2.37\ mm$$

B
$$4.74\ mm$$

C
$$10.54\ mm$$

D
$$5.44\ mm$$

Solution
Question 8
1 / -0

The Young's double slit experiment is done in a medium of refractive index $$4/3$$. A light of $$600\ nm$$ wavelength is falling on the slits having $$0.45\ mm$$ separation. The lower slit $$S_{2}$$ is covered by a thin glass sheet of thickness $$10.4\ \mu m$$ and refractive index $$1.5$$. The interference pattern is observed on a screen placed $$1.5\ m$$ from the slits as shown in figure.
Find the light intensity at point $$O$$ relative to the maximum fringe intensity.

A
$$3/4I_{max}$$

B
$$3/14I_{max}$$

C
$$4/3I$$

D
$$13/4I_{max}$$

Solution
Question 9
1 / -0

Four identical monochromatic sources A, B, C, D as shown in the figure produce waves of the same wavelength $$\lambda$$ and are coherent. Two receiver $$R_1$$ and $$R_2$$ are at great but equal distances from B. Which of the two receivers picks up the larger signal?

A
$$R_1$$

B
$$R_2$$

C
$$R_1 \,and \,R_2$$

D
None of these

Solution

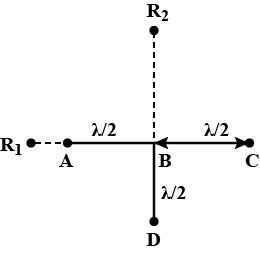
Consider the disturbances at $$R_1$$ which is at distance d from A. Let the wave at $$R_1$$ because of A be $$y_A \, = \, a \, cos \, \omega t.$$ The path difference of the signal from A with that from B is $$\lambda/2$$ and hence the phase difference is $$\pi$$.
Thus, the wave at $$R_1$$ because of B is
$$y_B \, = \, a \, cos \, (\omega t \, - \, \pi) \, = \, -4 \, cos \, \omega t.$$
The path difference of the single from C with that from A is $$\lambda$$ and hence, the phase difference is $$2\pi$$.
Thus, the wave at $$R_1$$ because of C is $$y_c \, = \, a \, cos \, \omega t$$.
The path difference between the signals from from D with that of A is
$$P \, = \, R_1D \, - \, R_1A \, = \, \sqrt{(R_1B)^2 \, + \, (BD)^2} \, - \, (R_1B \, - \, AB)$$
$$\sqrt{d^2 \, + \, \left(\dfrac{\lambda}{2} \right )^2} \, -(d \, - \, \lambda/2) \, = \, d \, \left(1 \, + \, \dfrac{\lambda^2}{4d^2} \right )^{1/2} \, -d \, + \, \dfrac{\lambda}{2}$$
$$d \left(1 \, + \, \dfrac{\lambda^2}{8d^2} \right ) \, -d \, + \, \frac{\lambda}{2} \, = \, \dfrac{\lambda^2}{8d} \, + \, \dfrac{\lambda}{2}$$
If d > > $$\lambda$$, the path difference $$- \, \dfrac{\lambda}{2}$$ and hence the phase difference is $$\pi$$.
$$\therefore \, y_D \, = \, -a \, cos \, \omega t.$$
Thus, the single picked up at $$R_1$$ is
$$y \, = \, y_A \, + \, y_B \, + \, y_C \, + \, y_D \, = \, 0$$
Let the signal picked up at $$R_2$$ from B be $$y_B \, = \, a_1 \, cos \, \omega t.$$
The path difference between signal at D and that at B is $$\lambda/2$$
$$\therefore \, y'_D \, = \, -a_1 \, cos \, \omega t$$
The path difference between signal at A and B is
$$\sqrt{(d)^2 \, + \, \left(\dfrac{\lambda}{2} \right)^2} \, -d \, = \, d\left(1 \, + \, \dfrac{\lambda^2}{4d^2} \right )^{1/2} \, -d \, = \, \dfrac{\lambda^2}{8d}$$
$$\therefore$$ The phase difference is
$$\dfrac{2\pi}{\lambda} \cdot \dfrac{\lambda^2}{8d} \, = \, \dfrac{\pi \lambda}{4d} \, = \, \phi \, ~ \, 0.$$
Hence, $$y_A \, = \, a_1 \, cos \, (\omega t \, ~ \, \phi)$$
similarly, $$y'_C \, = \, a_1 \, cos \, (\omega t \, - \, \phi)$$
$$\therefore$$ Signal picked up by $$R_2$$ is
$$y'_A \, + \, y'_B \, + \, y'_C \, + \, y'_D \, = \, y' \, = \, 2a \, cos \, (\omega t \, ~ \, \phi)$$
$$[\because \, y'_B \, + \, y'_D \, = \, 0]$$
$$\therefore \, |y|^2 \, = \, 4a^2_1 \, cos^2 \, (\omega t \, - \, \phi)$$
$$\therefore \, <I> \, = \, 2a^2_1$$
Thus $$R_2$$ picks up the large signal.
Question 10
1 / -0

A glass plate of refractive index $$1.5$$ is coated with a thin layer of thickness $$t$$ and refractive index $$1.8$$. Light of wavelength $$\lambda$$ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer and the two reflected rays interfere. Write the condition for their constructive interference. If $$\lambda = 648\ nm$$, obtain the least value of $$t$$ for which the rays interfere constructively.

A
$$90nm$$

B
$$40nm$$

C
$$30nm$$

D
$$45nm$$

Solution

$$\textbf{Given}:$$ $$\mu(glass)=1.5$$, $$\mu(thin layer) = 1.8$$, $$\lambda = 648nm$$

$$\textbf{Solution}"$$
Path difference between rays reflected from upper and lower faces of layer $$= 2 \mu t$$ (for normal incidence)
Path difference due to reflection form denser (upper) surface Is $$\dfrac{\lambda}{2}$$.
condition of constructive interference (or maxima) is
$$2 \mu t +\dfrac{\lambda}{2} = n \lambda t = \dfrac{1}{2 \mu} (2 n - 1) \dfrac{\lambda}{2} = \dfrac{(2 n -1)\lambda}{4 \mu}$$ , n = 1, 2, 3,...
For least thickness, n = 1.
$$\therefore t_{min} = \dfrac{\lambda}{4 \mu} = \dfrac{648}{4 \times 1.8} nm = 90 nm$$

$$\textbf{Hence A is the correct option}$$