Magnetism and Matter Test 30

Result

Magnetism and Matter Test 30

Score
-
out of -
Rank
-
out of -

TIME Taken - -

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Weekly Quiz Competition

Question 1
1 / -0

Potential energy of a bar magnet of magnetic moment $$M$$ placed in a magnetic field of induction $$B$$ Such that it makes an angle $$\theta$$ with the direction of $$B$$ is (take $$\theta={90}^{o}$$ as datum)

A
$$-M\ B \sin {\theta}$$

B
$$-M\ B \cos {\theta}$$

C
$$M\ B (1-\cos {\theta})$$

D
$$M\ B (1+\cos {\theta})$$

Solution

$$dw=-\tau.d\theta=-MB\sin\theta.d\theta$$ where $$\theta$$ is angle between $$\vec{M}$$ and $$\vec{B}$$.
Since work done=Potential energy lost
$$\implies du=-dw=MB\sin\theta.d\theta$$
$$u=\int MB\sin\theta.d\theta=-MB\cos\theta$$
Question 2
1 / -0

Figure shows a square loop of side $$1m$$ and resistance $$1\Omega$$. The magnetic field on left side of line PQ has a magnitude $$B=1.0T$$. The work done in pulling the loop out of the field uniformly in $$1s$$ is

A
$$1J$$

B
$$10J$$

C
$$0.1J$$

D
$$100J$$

Solution

$$V=\dfrac l{t}=1m/s$$
$$W=Power\times Time$$
$$=\dfrac{(Blv)^2}{R}\times t$$
$$=\dfrac{B^2l^2}{Rt}=\dfrac{1^2\times 1^4}{1\times 1}=1J$$
Question 3
1 / -0

A circular loop of area $$1$$ $$cm^2$$, carrying a current of $$10$$A, is placed in a magnetic field of $$0.1$$T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is?

A
Zero

B
$$10^{-4}$$N-m

C
$$10^{-2}$$N-m

D
$$1$$N-m

Solution

As Torque is given by
$$T = NBiA\sin \theta$$
Area $$= 1cm^2$$
Current $$= 10A$$
Magnetic field $$= 0.1T$$
$$\theta = 0$$
$$T= 1\times 10\times 0.1\times \sin 0$$
$$= 1 \times 0$$
$$T = 0$$
Question 4
1 / -0

A bar magnet is made to fall through a vertical copper tube. The speed ($$v$$) of the magnet as a function of time ($$t$$) is best represented by

A
$$a$$

B
$$b$$

C
$$c$$

D
$$d$$

Solution

Hint: Lenz’s law dictates the behaviour of a magnet in a metallic tube and it states that “The current induced in a circuit due to a change in a magnetic field is directed to oppose the change in flux and to exert a mechanical force which opposes the motion.

Step 1: $$\textbf{Explanation:}$$

$$\bullet $$When a bar magnet is subjected to free fall through a long, hollow, metallic tube then the change in the magnetic flux due to the non-uniformity of the magnetic field of the magnet results in formation of Eddy currents.

$$\bullet $$So, as per the Lenz’s law, the eddy currents thus generated oppose the force which causes the initial change in flux, i.e. gravitational force, with a retarding force. This retarding force leads to reducing acceleration of the falling magnet.

$$\bullet $$Due to the lessening of the acceleration, the magnet eventually attains $$0$$ acceleration (i.e. reaches terminal velocity) and falls through the tube at $$0$$ acceleration.

$$\bullet $$As per the graph, line ‘$$b$$’ shows the motion of magnet as per the above reasons.
$$\textbf{Hence, the correct option is (B)}$$
Question 5
1 / -0

The figure shows the various positions (labelled by subscripts) of small magnetised needles P and Q. The arrows show the direction of their magnetic movement.configuration corresponds to the lowest potential energy among all the configurations shown

A
$$PQ_3$$

B
$$PQ_4$$

C
$$PQ_5$$

D
$$PQ_6$$

Solution

Given, two small magnetic needle P and Q respectively,

So, At $$pQ_6$$ when all the movements are in the parallel direction potential will be minium.
Question 6
1 / -0

A conductor behave as a super conductor

A
Above critical temperature

B
At critical temperature

C
At $${100}^{o}C$$

D
At boiling point of that metal

Solution

Superconductors are conductors with exactly zero resistance. Conductors put under temperature above critical temperature behave as a super conductor.
Question 7
1 / -0

A short-circuited coil is placed in a time-varying magnetic field. Electrical power is dissipated due to the current induced in the coil. If the number of turns were to be quadrupled and the wire radius halved, the electrical power dissipated would be:

A
Halved

B
The same

C
Doubled

D
Quadrupled

Solution

$$P=\frac{\varepsilon ^2}{R}$$
where,$$\varepsilon =induced emf=-\frac{d\phi}{dt}$$
$$\phi=NBA$$
$$\varepsilon =NA\frac{dB}{dt}$$
also, $$R\propto \frac{l}{r^2}$$
where ,R=resistance and r=radius of wire
$$P\propto \frac{N^2r^2}{l^2}$$
$$\frac{P_1}{P_2}=1$$
$$P_1=P_2$$
This means if the number of turns were quadrupled and the wire radius halved, the electrical power dissipated would be remains same.
Question 8
1 / -0

A long straight wire of circular cross-section is made of a non-magnetic material. The wire is of radius $$a$$.The wire carries a current $$I$$ which is uniformly distributed over its cross-section. The energy stored per unit length in the magnetic field contained within the wire is

A
$$U=\dfrac {\mu_{0}I^{2}}{8 \pi}$$

B
$$U=\dfrac {\mu_{0}I^{2}}{16 \pi}$$

C
$$U=\dfrac {\mu_{0}I^{2}}{4 \pi}$$

D
$$U=\dfrac {\mu_{0}I^{2}}{2 \pi}$$

Solution

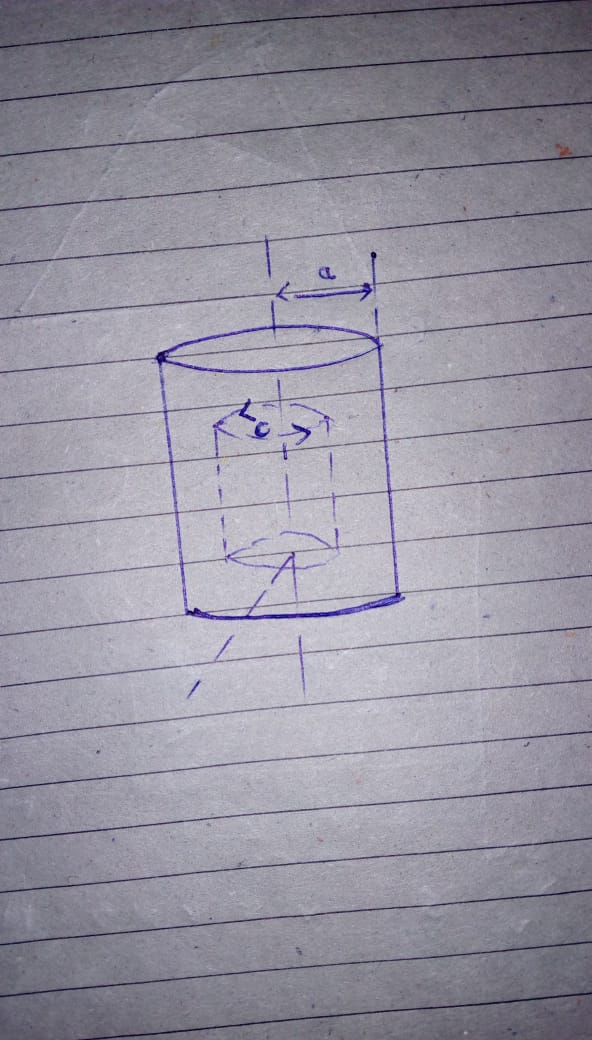
We use a standard right handed coordinate system $$\left( {r,\phi ,z} \right)$$
Since the current is entirely axial, the Boit-savart law implies that $${B_z} = 0$$ every where

Symmetry consideration require that the $$r$$ and $$\phi $$ components of $$B$$ depends upon
$$r:B={ B_{ r } }\left( r \right) \hat { r } +{ B_{ \phi } }\left( r \right) \hat { \phi } $$

Now apply Gauss's law for magnetic field to the coaxial cylindrical surface $$S$$, which has length $$l$$ and radius $$r$$

$$0 = \int_S {B.da = {B_r}\left( r \right)2\pi rl} $$

Therefore, $${B_r}\left( r \right) = 0$$

Amper's law to coaxial circular path $$C$$
$$\oint_c {B.dI = 2\pi r{B_\phi }\left( r \right) = {\mu _0}i\left( r \right)} $$ $$........(1)$$

Here $$i(r)$$ is the current passing through the surface enclosed by $$C$$

Since, the current density is uniform we have,
$$\begin{array}{l} \frac { { i\left( r \right) } }{ i } =\frac { { \pi { r^{ 2 } } } }{ { \pi { a^{ 2 } } } } \\ i\left( r \right) =\frac { { { r^{ 2 } }i } }{ { { a^{ 2 } } } } \end{array}$$ $$...(2)$$

Equation $$1$$ and $$2nd$$ implies that
$${B_\phi }\left( r \right) = \frac{{{\mu _0}ir}}{{\left( {2\pi {a^2}} \right)}}$$

Now integrate the magnetic energy density over the volume of the wire. The magnetic energy $$d{U_m}$$ contained in the cylindrical shell of length $$1$$, inner radius $$r$$ and outer radius $$r+dr$$ is

$$\begin{array}{l} d{ U_{ m } }={ \in _{ m } }UV=\frac { { { B_{ \phi } }^{ 2 }\left( r \right) } }{ { 2{ \mu _{ 0 } } } } 2\pi r1dr \\ =\frac { { { \mu _{ 0 } }{ i^{ 2 } }1 } }{ { 4\pi { a^{ 4 } } } } { r^{ 3 } }dr \end{array}$$

Hence, the magnetic energy per unit length contained in the wire is

$$\frac{{{U_m}}}{1} = \frac{1}{1}\int {d{U_m} = \frac{{{\mu _0}{i^2}}}{{4\pi {a^4}}}\int_0^a {{r^3}dr = \frac{{{\mu _0}{r^2}}}{{4\pi {a^4}}}\left( {\frac{{{r^4}}}{4}|_0^a} \right)} } $$
$$ = \frac{{{\mu _0}{i^2}}}{{16\pi }}$$

Hence, Option B is the correct answer.
Question 9
1 / -0

Two protons enter a region of the transverse magnetic field. What will be the ratio of the time period of revolution if the ratio of energy is $$2\sqrt 2 :\sqrt 3 ?$$

A
$$2\sqrt 2 :\sqrt 3 $$

B
$$\sqrt 3 :2\sqrt 2 $$

C
$$3:8$$

D
$$1:1$$

Solution

The time period of revolution when proton enter a region of the transverse magnetic field.

$$T=2\pi\sqrt{\dfrac{mr}{qBv}}$$

where, $$q=$$ charge of proton

$$B=$$ transverse magnetic field

$$v=$$speed of proton

$$r=$$ radius of circular path.

Hence,

$$T\alpha\dfrac{1}{\sqrt{v}}$$.. . . .(1)

Kinetic energy,

$$K=\dfrac{1}{2}mv^2$$

$$v\alpha\sqrt{K}$$.. . . . . . . .(2)

From equation (1) and (2), we conclude that,

$$T\alpha\dfrac{1}{K}$$

$$K_1:K_2=2\sqrt{2}:\sqrt{3}$$ (Given)

$$T_1:T_2=\sqrt{3}:2\sqrt{2}$$

The correct option is B.
Question 10
1 / -0

When two co axis coil having same current in same direction are brought close to each other then the value of current in both coils:

A
Increase

B
Decreases

C
First increases and then decreases

D
Remain same

Solution