Ray Optics and Optical Test

Result

Ray Optics and Optical Test - 27

Score
-
out of -
Rank
-
out of -

TIME Taken - -

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Weekly Quiz Competition

Question 1
1 / -0

A tall man of height 6 feet, want to see his full image. Then required minimum length of the mirror will be -

A
12 feet

B
3 feet

C
16 feet

D
Any length
Question 2
1 / -0

A fish looking up through the water sees outside world contained in a circular horizon. If the refractive index of water is 4/3 and fish is 12 cm below the surface, the radius of the circle is centimetres is

A
$$12\times 3\times \sqrt 5$$

B
$$4\times \sqrt 5$$

C
$$12\times 3\times \sqrt 7$$

D
$$12\times 3/ \sqrt 7$$
Question 3
1 / -0

The index of refraction of diamond is 2.0. The velocity of light in diamond in cm/s is -

A
$$6\times 10^{10}$$

B
$$2\times 10^{10}$$

C
$$3\times 10^{10}$$

D
$$1.5\times 10^{10}$$

Solution

$$V=\dfrac {3\times 10^8}{2}=1.5\times 10^8m/s=1.5\times 10^{10}cm/s$$
Question 4
1 / -0

Chromatic aberration(distance between the focal lengths for extreme wavelengths) of a convex lens can be reduced by(Assume lenses are kept in vacuum)

A
Adding a concave lens

B
Adding a convex lens

C
Decreasing focal length by squeezing it

D
Decreasing aperture without changing it curvature

Solution

It can be reduced by "Decreasing aperture without changing it curvature"
option $$D$$ is correct
Question 5
1 / -0

A ray of light is incident normally on the first refracting face of the isosceles prism of refracting angle A. The ray of light comes out at grazing emergence. If one half of the prism (shaded position) is knocked off, the same ray will :

A
emerge at an angle of emergence $$sin^{-1} \left ( \frac{1}{2} sec A/2 \right )$$

B
not emerge out of the prism

C
emerge at an angle of emergence $$sin^{-1} \left ( \frac{1}{2} sec A/4 \right )$$

D
None of these

Solution

Given: A ray of light is incident normally on the first refracting face of the isosceles prism of refracting angle A. The ray of light comes out at grazing emergence.
To find the angle emergence angle of the same if one half of the prism is knocked off
Solution:
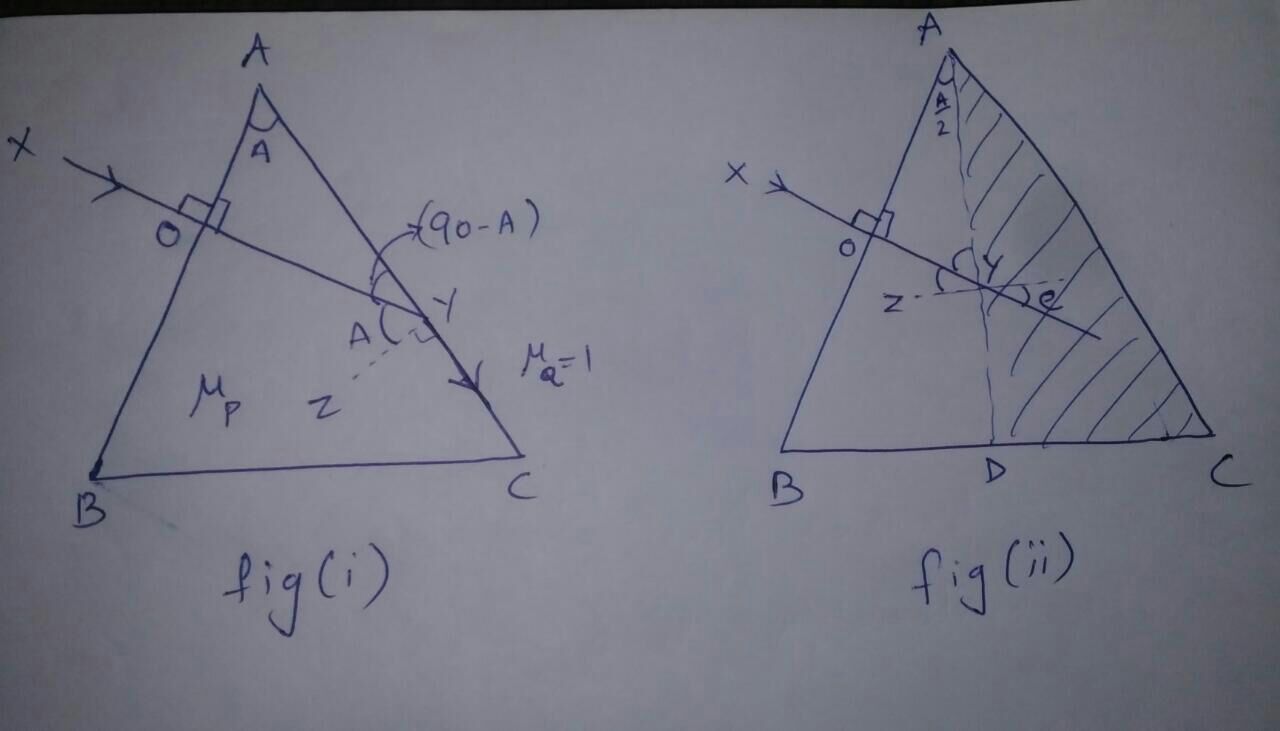
Case (i): when ray of light is incident normally on first refracting face of the isosceles prism. (refer fig(i))
Let the ray X is incident normally on first refracting face, AB of the isosceles triangle ABC.
As it it given refracting angle, $$\angle {XYZ} = A$$
Hence $$\angle XYA = (90-A)$$
In right angled traingle $$AOY$$
$$180^\circ = \angle AOY + \angle OYA +\angle YAO\\\implies \angle YAO=180-90-(90-A)=A.........(i)$$
And as the comes out at grazing emergence hence angle of emergence in this case is $$90^\circ$$
So we know,
$$\mu_1\times \sin i=\mu_2\times \sin e........(ii)$$.
Here $$\mu_1=\mu_p$$ refractive index of prism,
$$\mu_2=\mu_a=1$$ as it is refractive index of air,
angle of incidence $$i=A$$ (given) and
angle of emergence $$e=90^\circ$$ (given).
Therefore, by substituting these values in equation (ii), we get
$$\mu_p\times \sin A=1\times \sin 90\\\implies \mu_p=\dfrac 1{\sin A}.........(iii)$$

Case (ii): when half of the prism is knocked off (refer fig(ii))
Then $$\angle YAO=\dfrac A2$$
In right-angled triangle,
$$180^\circ=\angle AOY + \angle OYA +\angle YAO\\\implies \angle OYA=180-90-\left(\dfrac A2\right)\\\implies \angle OYA=90-\dfrac A2$$
And angle of incidence, $$\angle XYZ=i=90-\left(90-\dfrac A2\right)=\dfrac A2$$
So the equation (ii), in this case will become
$$\mu_p\times \sin \left(\dfrac A2\right)=\mu_a\times \sin e\\\implies \dfrac 1{\sin A}\times \sin \left(\dfrac A2\right)=\sin e$$
$$\sin e = \dfrac {\sin \left(\dfrac A2\right)}{2\sin \left(\dfrac A2\right)\cos \left(\dfrac A2\right)}$$ [$$\because \sin A=2\sin \left(\dfrac A2\right)\cos \left(\dfrac A2\right)$$]
Therefore,
$$\sin e=\dfrac{\sec \left(\dfrac A2\right)}2$$ [$$\because \sec A=\dfrac 1{\cos A}$$]
Hence incident ray will emerge at angle of emergence
$$e=\sin^{-1} \left\{\dfrac 12 \sec \left(\dfrac A2\right)\right\}$$
Question 6
1 / -0

A ray of light falls on the surface of spherical glass paperweight making an angle $$\alpha$$ with the normal and is refracted in the medium at an angle $$\beta$$. The angle of deviation of the emergent ray from the incident ray is

A
$$\left( \alpha -\beta \right) $$

B
$$ 2\left( \alpha -\beta \right) $$

C
$$ \dfrac { \left( \alpha -\beta \right) }{ 2 } $$

D
$$ \left( \alpha +\beta \right) $$

Solution

As seen in the figure at the first interface the deviation is $$\alpha - \beta$$ and at the second interface the angle of incidence is $$\beta$$ again the deviation is $$\alpha - \beta$$
total deviation is $$2(\alpha - \beta)$$ .
Question 7
1 / -0

A ray of light falls on a prism $$ABC (AB=BC)$$ and travels as shown in the figure. The refractive index of the material of prism should be at least :

A
$$ \dfrac { 4 }{ 3 } $$

B
$$ \sqrt { 2 } $$

C
$$\dfrac { 3 }{ 2 } $$

D
$$ \sqrt { 3 } $$

Solution

This is a right angled isosceles triangle
$$\angle A=\angle C={ 45 }^{ 0 }\\ and\quad \angle B={ 90 }^{ 0 }$$

the total internal reflection takes places at critical angle $$\theta $$

$$sin\theta \ge \dfrac { 1 }{ \mu } \\ \mu \ge \dfrac { 1 }{ sin\theta } $$

$$\theta =critical\quad angle\quad (incident\quad angle)$$

here critical angle $$\theta =i={ 45 }^{ 0 }$$

thus $$\mu \ge \sqrt { 2 } $$

Option B is correct.
Question 8
1 / -0

The cause of mirage formation in desert areas is

A
The refractive index of atmosphere decreases with decrease in height

B
The refractive index of atmosphere increases with decrease in height

C
The refractive index of atmosphere does not change with height

D
Scattering

Solution

The reason for mirage formation is "The refractive index of atmosphere increases with decrease in height" and hence the rays get totally refracted and forms a mirage.

As we go down in the atmosphere, the air gets denser and hence the velocity in that medium decreases. Since refractive index $$\mu = \dfrac{c}{v}$$. Hence, the refractive index increases as we decrease height.
Question 9
1 / -0

A beam of light, consisting of red, green and blue colours, is incident on a right-angled prism, as shown. the refractive indices of the material of the prism for the above red, green and blue wavelengths are 1.39 1.44 and 1.47 respectively. The prism will :

A
separate part of the red colour from the green and blue colours

B
separate part of the blue colour from the red and green colours

C
separate all the three colours from one another

D
not separate even partially any colour from the other tow colours

Solution

The angle of incidence of all the rays is $$ { 45 }^{ \circ }$$ at the hypotenuse. For a critical angle of $$ { 45 }^{ \circ }$$, the refractive index must be
$$ { \left( \sin { { 45 }^{ \circ } } \right) }^{ -1 }=\sqrt { 2 } =1.414$$

For red light, $$\mu =1.39<1.414.$$. hence, its critical angles are <$$ { 45 }^{ \circ }$$. therefore, red light will pass through the surface into air.

For green and blue lights, $$ \mu >1.414.$$. Hence, their critical angles are $$ <{ 45 }^{ \circ }$$. They will be reflected internally and emerge from the surface at the bottom.
Question 10
1 / -0

The angle of the prism for which there is no emergent ray will be, if its critical angle is $$ { i }_{ c }$$

A
greater than $$ { i }_{ c }$$

B
less than $$ { i }_{ c }$$

C
$$ { 2i }_{ c }$$

D
greater than $$ { 2i }_{ c }$$

Solution

Applying snell's law at the two refracting surfaces,
$$\sin i=\mu \sin r_{1}$$
$$\sin e=\mu \sin r_{2}$$
Also $$A=r_{1}+r_{2}$$
For no emergent ray, $$e=90^{\circ}$$
hence, $$r_{2}=i_{c}$$
Also for there to be no emergent ray in any case, $$r_{1}$$ can have the maximum value in the limiting case.
For this to happen, $$i=90^{\circ}$$ in the case.
hence $$r_{1}=i_{c}$$
hence, $$A>2i_{c}$$