Electrostatic Potential Test - 1

CONCEPT : 

• The amount of work done in moving a unit positive charge in an electric field from infinity to that point without accelerating the charge against the direction of the electric field is electrostatic potential.
• Volt is the unit of electrostatic potential.

EXPLANATION :

• The force applied to must the charge must be equal to the electrostatic repulsive force experienced for the charge.
• The work done is to move the charge from point a to b is given by

 \(W_{ab} = -\int_{a}^{b}F_{E}.dr\)

• The work done is against the electrostatic repulsive force and is stored as the potential energy  
• Hence option2  is the answer

The correct answer is option 2) i.e. 5 V.

CONCEPT:

• Electric potential: The electric potential is also known as voltage (V), is the difference in potential energy per unit charge between two points in an electric field. 

The electric potential at any point around a point charge is given as:

 \(V = \frac{kQ}{r}\)

Where Q is the point charge, r is the distance from the point charge and k is the constant with a value equal to 9\(\times\)10⁹ Nm²/C².

• Principle of conservation of charge: Conservation of charge is based on the principle that the total electric charge in an isolated system remains constant.

​CALCULATION:

Given that:

The potential of the large liquid drop (V_L) = 20 V

From the principle of conservation of charge,

Potential due to 8 small drops = Potential due to large drop

8\(\times\)VS = VL     

8\(\times\)q = Q      ----(1)

Since the large drop is combined from 8 drops,

Volumes of 8 drops = volume of a large drop

\(8\times\frac{4}{3}\:\pi r^3 = \frac{4}{3}\:\pi R^3 \)

\(\Rightarrow 2r =R\)      ----(2)

From (1),

\(V_S = \frac{kq}{r}\) and \(V_L = \frac{kQ}{R}\)

\(\frac {V_S}{V_L} = \frac{\frac{8kq}{r}}{\frac{kQ}{R}} = \frac {q}{Q} \times \frac{R}{r}\)          

\(\frac {V_S}{20} = \frac {q}{8q} \times \frac{2r}{r} = \frac{1}{4}\)          (Substituting 2r = R)

The potential of a single drop, V_S = 5 V 

CONCEPT:

• Electric potential is equal to the amount of work done per unit charge by an external force to move the charge q from infinity to a specific point in an electric field.

\(⇒ V=\frac{W}{q}\)

• Potential due to a single charged particle Q at a distance r from it is given by:

\(⇒ V=\frac{Q}{4\piϵ_{0}r}\)

Where, 

ϵ0 is the permittivity of free space and has a value of 8.85 × 10-12 F/m in SI units

EXPLANATION:

• The potential due to a dipole is given by

\(\Rightarrow V= \frac{p cosθ}{4 \pi \epsilon_0 r^2}\)

• At the axial point, θ is zero, hence cosθ = 1, V is non-zero.
• At the equatorial point, θ is \(\frac {\pi}{2}\), hence cosθ = 0, V is zero.
• Therefore option 3 is correct

CONCEPT:

Electric potential (V):

• The potential difference between two points in an electric field may be defined as the amount of work done in moving a unit positive charge from one point to the other against the electrostatic force i.e.,

\({\rm{Electric\;potential\;}}\left( {\rm{V}} \right) = \frac{{{\rm{Work\;done\;}}\left( {\rm{W}} \right)}}{{{\rm{Charge\;}}\left( {\rm{q}} \right)}}\)

• The electric potential V at a point P due to point charge +q at a distance r is given by

\(V=\frac{1}{{4{\rm{\Pi }}\varepsilon_o }}\frac{q}{r}\)     

Where \(\frac{1}{{4{\rm{\Pi }}\varepsilon_o}}\) is a constant = 9 × 10⁹ Nm²/C², q is charge and r is distance from charge particle.

CALCULATION::

Given - Charge (q) = 25 × 10^-10 C and Distance (r) = 5m

•  The electric potential V at a point P due to point charge +q at a distance r is given by

\(⇒ V=\frac{1}{{4{\rm{\Pi }}\varepsilon_o }}\frac{q}{r}\)

\(⇒ V = \;\frac{{9 \times {\rm{\;}}{{10}^9} \times 25 \times {\rm{\;}}{{10}^{ - 10}}}}{5}\)

CONCEPT:

• Electrostatic Potential energy between two charges q1 and q2 at the distance of R is given by:

\(V=\frac{1}{4\pi ϵ_0}\frac{q_1q_2}{R} \)

where F is the electrostatic force, q₁ and q₂ are the charges, and ϵ0 is the electrical permittivity of vacuum.

• Electrostatic Potential energy is a scalar quantity.

CALCULATION:

• ​Given that The charges Q + q and + q are placed at the vertices of an equilateral triangle of side l. and the net electrostatic potential energy of the system is zero.

• Since Electrostatic Potential is a scalar quantity, 

\(V = V_{AB}+V_{BC}+V_{CA}\)

\(V=\frac{1}{4\pi ϵ_0}\frac{Qq}{l} +\frac{1}{4\pi ϵ_0}\frac{q(q)}{l} +\frac{1}{4\pi ϵ_0}\frac{Q(q)}{l} \)

V = 0 (Given)

\(0=\frac{1}{4\pi ϵ_0}\frac{Qq}{l} +\frac{1}{4\pi ϵ_0}\frac{q(q)}{l} +\frac{1}{4\pi ϵ_0}\frac{Q(q)}{l} \)

0 = Qq + q(q) + Q(q)

Q = \(\frac{{ - q}}{2}\)

So the correct answer is option 1.

CONCEPT:

• Equipotential surface: Any surface that has the same electric potential at every point on it is called an equipotential surface.
• Relationship between the electric field (E), electric potential (V) and distance (r) is given by -

• \(dE = - \frac{{dV}}{{dr}}\)
• The electric field is a derivative of potential difference.
• The negative sign shows that the direction of E is opposite to the direction of dv i.e., dv decrease along the direction of E.

EXPLANATION:

• The electric field is always normal to the equipotential surface at every point.
• If the field were not normal to the equipotential surface, it would have a non-zero component along the surface.
• So to move a test charge against this component, work would have to be done.
• But there is no potential difference between any two points on an equipotential surface and consequently, no work is required to move a test charge on the surface.
• Hence the electric field must be normal to the equipotential surface at every point. Therefore option 4 is correct.

CONCEPT:

• Electric lines of forces constitute the electric field and vice versa.
• Electric lines of force:  Inside the electric field, The path along which a unit positive charge will move if it is free to do so is called electric lines of force.
  • The tangent at any point to these lines gives the direction of the electric field at that point.
• Electric lines of force always flow from higher potential to lower potential.
• If we move perpendicular to these lines, the electric potential doesn't change.

EXPLANATION:

• Electric lines of force always flow from higher potential to lower potential.
• So in the given figure in the question, 
• If we move from labelled point to the right side, the potential will decrease.
• If we move from label to the left side, the potential will increase.
• If we move perpendicular to these lines, the electric potential doesn't change.

​

• So there are 3 more points other than the labelled point which will be at the same potential. (Perpendicular to the electric field).
• So the correct answer is option 4.

CONCEPT:

Electrical potential:

• The electric potential at any point in the electric field is defined as the amount of work done in moving a unit positive test charge from infinity to that point without acceleration.

\(\Rightarrow V=\frac{kQ}{r}\)    

Where V = electric potential at a point, k = 9×109 N-m2/C2, Q = charge, and r = distance of a point from the center of the charge

Surface charge density:

• According to electromagnetism, surface charge density is defined as a measure of electric charge per unit area of the surface.

​\(\Rightarrow \sigma =\frac{Q}{A}\)  

Where σ = surface charge density, Q = charge and A = surface area

CALCULATION:

• The electric potential on the surface of sphere A is given as,

CONCEPT:

• Equipotential surface: Any surface that has the same electric potential at every point on it is called an equipotential surface.
• By definition, the potential difference between two points B and A = work done in carrying unit positive test charge from A to B, i.e., V_B – V_A = W_AB
• If points A and B lies on an equipotential surface, then V_B = V_A

⇒W_AB = V_B – V_A = 0

• Hence, no work is done in moving the test charge from one point of equipotential surface to the other.

EXPLANATION:

• From above it is clear that net work done in carrying change from A to B is zero, B to C is zero because W = q(dV) and V is the same on this equipotential Surface
• All the mentioned points are lying on an equipotential surface. Hence the total work done will be zero. Therefore option 3 is correct.

CONCEPT:

Force one a charge q in an electric field is defined as 

⇒ F = Eq

The work done by this force in moving the charge by a distance d along the direction of electrostatic force (along the electric field) is

⇒ W = F.d = Eq.d

The work done by external force in moving this charge by a distance d along the direction of the electrostatic field is

⇒ Wext = - W = - Eq.d

By definition, the change in potential energy in moving the charge in an electrostatic field is equal to the work done by external forces

\(\Rightarrow \bigtriangleup U = W_{ext} = -Eq.d\)

Electric potential is equal to the amount of work done per unit charge by an external force to move the charge q from infinity to a specific point in an electric field

\(\Rightarrow V=\frac{W_{ext}}{q}\)

Therefore the relation between electric potential and electric potential energy is given by

\(\Rightarrow \bigtriangleup U = W_{ext} = Vq\)

EXPLANATION:

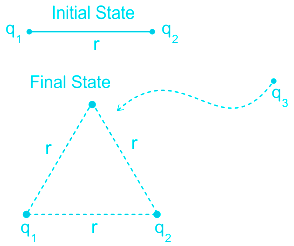
The potential energy of the initial state is the energy due to the interaction between q₁ and q₂. It is given as U

\(\Rightarrow U=\frac{Q_1 Q_2}{4\pi \epsilon_0 R}\)\(\Rightarrow U_{12}=\frac{q_1 q_2}{4\pi \epsilon_0 r} =U\)

When the charge q₃ is introduced, the increase in potential energy of the system is due to its interaction with q₁ and q₂

The potential energy due to the interaction between q₂ and q₃ is given by

\(\Rightarrow U_{23}=\frac{q_2 q_3}{4\pi \epsilon_0 r} \)

The potential energy due to the interaction between q₃ and q₁ is given by

\(\Rightarrow U_{31}=\frac{q_3 q_1}{4\pi \epsilon_0 r} \)

Since q₁, q₂, and q₃ all are equal, thus

\(\Rightarrow U_{12}=U_{23}=U_{31}=U\)

The total potential energy of the system when the three charges make an equilateral triangle is 

\(\Rightarrow U_{total}=U_{12}+U_{23}+U_{31}=U+U+U=3U\)

Therefore option 4 is correct