Mechanical Engineering Test

Result

Mechanical Engineering Test - 3

Score
-
out of -
Rank
-
out of -

TIME Taken - -

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Weekly Quiz Competition

Question 1

2 / -0.66

Directions For Questions

Consider the problem of assigning five operators to five machines. The assignment costs are given below.

Operators	Machines
Operators	A	B	C	D	E
I	10	3	10	7	7
II	5	9	7	11	9
III	13	18	2	9	10
IV	15	3	2	7	4
V	16	6	2	12	12

...view full instructions

Assign the operators to different machines so that the total cost is minimized. Find the value of minimum cost.

23

22

20

24 Solution

Explanation:

In the assignment model, the following steps are involved to find the opportunity cost matrix

10	3	10	7	7
5	9	7	11	9
13	18	2	9	10
15	3	2	7	4
16	16	2	12	12

1.Subtract the smallest element of each row from every element of the corresponding row

7	0	7	4	4
0	4	2	6	4
11	16	0	7	8
13	1	0	5	2
14	4	0	10	10

Now, subtract the smallest element in each column from every element of the corresponding column.

7	0	7	0	2
0	4	2	2	2
11	16	0	3	6
13	1	0	1	0
14	4	0	6	8

Now, make an assignment in the opportunity cost matrix. For assigning initially check single zero rows and assign the value to it and then cut the remaining zero in the column, then find the column with single zero and then repeat this procedure till all the assignment is done

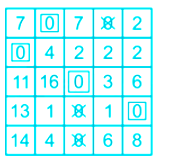
Now, if the no-of allocation is exactly equal to the size of matric, then the current solution is optimum otherwise perform optimality

In this case no-of allocations = 4, so the solution is not optimum

Now, for optimality

i) Mark all rows for which assignment have not been made (5^th row)

ii) Mark all columns which have unassigned zero in the marked (column 3)

iii) Mark all row which have an assignment in the marked column (row 3)

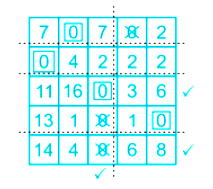
Now, draw minimum no. of lines through the unmarked row and through the marked column to cover all zeros at least once.

Now, select the smallest element that does not have a line through then, subtract form all the elements that do not have a line through them, add it to every element that lies at the intersection of two lines and leave the remaining element matrix unchanged. Then make allocations in the new opportunity cost matrix.

Here smallest element is in 3^rd row (3)

7	0	10	0	2
0	4	5	2	2
8	13	0	0	3
13	1	3	1	0
11	1	0	3	5

Now making assignment

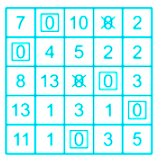
The final allocation is

I - B, II → A, III → D, IV - E and V - C

Total cost = 3 + 5 + 9 + 4 + 2 = 23

Question 2
2 / -0.66

The expected life of a ball bearing subjected to a load of 9800 N and working at 1000 rpm is 3000 hours. What is the expected life of the same bearing for a similar load of 4900 N and speed of 2000 rpm?

A
12,000 hours

B
6,000 hours

C
1,500 hours

D
Unchanged

Solution

Concept:

Load-life relationship:

The approximate rating of the service life of a ball or roller bearing is based on the given fundamental equation.
Question 3
2 / -0.66

The band brake shown in the figure is to have a maximum lining presure of 600 kPa, the drum is 350 mm in diameter, and the band width is 100 mm. The coefficient of friction is 0.25 and the angle of wrap is 270°. Band tensions of the brake are

A
3.2 kN, 6.3 kN

B
5.2 kN, 7.3 kN

C
4.2 kN, 5.4 kN

D
3.2 kN, 10.5 kN

Solution
Question 4
2 / -0.66

A 1 m³ tank containing air at 25°C and 500 kPa is connected through a valve to another tank containing 5 kg of air at 35°C and 200 kPa. Now the valve is opened, and the entire system is allowed to reach thermal equilibrium with the surroundings, which are at 20°C. final equilibrium pressure of air is:

A
112.5 kPa

B
60.5 kPa

C
284.12 kPa

D
284.12 bar

Solution
Question 5
2 / -0.66

A vapour absorption refrigeration system is a heat pump with three thermal reservoirs as shown in the figure. A refrigeration effect of 100 W is required at 250 K when the heat source available is at 400 K. Heat rejection occurs at 300 K. The minimum value of heat required (in W) is

A
167

B
100

C
80

D
20

Solution

T₂ = 250 K

T₁ = 300 K

T₃ = 400 K

Refrigerating effect : Q₂ = 100 W

In the case of VARS, the COP can be remembered directly.

Just apply a heat engine between the upper two temperatures and a refrigerator between lower two
Question 6
2 / -0.66

An inward flow reaction turbine has external and internal diameters as 2.0 m & 1.0 m respectively. The velocity of flow through the runner is constant & is equal to 3 m/s. Determine the discharge (in m³/s) through the runner, if width of the runner at inlet is 400 mm.

A
1.88

B
2.36

C
7.54

D
9.42

Solution

Concept:

Outward flow reaction turbine:

Question 7

2 / -0.66

A closed tank of constant volume containing a mixture of water and water vapour with dryness fraction 0.05. This system is heated externally such that the temperature changes from 293 K to 350 K. Using the following data, find the value of heat added into the system. Assume reversibility

State	u_f (kJ/kg)	u_g (kJ/kg)	h_f (kJ/kg)	h_g (kJ/kg)	v_f (m³/kg)	v_g (m³/kg)
T : 293 K	83.91	2402.3	83.84	2537.2	0.001	57.757
T : 350 K	313.99	2475.2	313.96	2634.6	0.00103	4.129

1626.05 kJ/kg

1650.04 kJ/kg

1000.03 kJ/kg

1200.07 kJ/kg

Solution

Concept:

Question 8
2 / -0.66

A
2

B
0

C
-2

D
3

Solution
Question 9
2 / -0.66

A hollow alloy tube 6 m long with an external diameter of 50 mm and internal diameter of 30 mm was found to extend 2.98 mm under a tensile load of 50 kN. Find safe load on the tube used as strut of both ends pined( Up to the nearest integer value) in KN. Take the factor of safety as 3.

A
2 kN

B
5 kN

C
6 kN

D
1 kN

Solution
Question 10
2 / -0.66

The maximum shear stress developed in the bar subjected to tensile stress (2σ) as shown in the figure will be_______.

A
σ

B
2σ

C
0.5σ

D
0.25σ

Solution