Mathematics Test - 10

Two equal and opposite direction forces \(f\) acting, and then value resulting force will be zero.

• Equal forces acting in opposite directions are called balanced forces.
• Balanced forces acting on an object will not change the object’s motion.
• When you add equal forces in opposite directions, the net force is zero.

Given,

\(A = 1\) kN

\(B = 1\) kN

By Lami's Theorem

\(\frac{A}{\sin \alpha}=\frac{B}{\sin \beta}=\frac{C}{\sin \gamma}\)

where \(A, B, C\) are the magnitudes of the three coplanar, concurrent and non-collinear vectors, and \(α, β, γ\) is the respective angle between them.

\(\frac{F}{\sin 60^{\circ}}=\frac{1}{\sin (90+60)^{\circ}}=\frac{1}{\sin (90+60)^{\circ}}\)

\(F=\frac{\sin 60^{\circ}}{\sin (90+60)^{\circ}}=1.73\) kN

According to Lami's Theorem:

\(\frac{P}{\sin \alpha}=\frac{Q}{\sin \beta}=\frac{R}{\sin \gamma}\)

Also,

\(\frac{T_{Q R}}{\sin (180-\alpha)^{\circ}}=\frac{W}{\sin (\beta+\alpha)^{\circ}}=\frac{T _{PR}}{\sin (180-\beta)^{\circ}}\)

\(\sin \left(180^{\circ}-\theta\right)=\sin \theta\)

Let \(T\) be tension is spring.

Applying Lami’s Theorem,

\(\frac{T}{\sin 90^{\circ}}=\frac{100}{\sin 120^{\circ}}=\frac{F}{\sin 150^{\circ}}\)

\(F=\frac{100 \sin 150^{\circ}}{\sin 120^{\circ}}\)

\(F=57.73 \mathrm{~N}\)

Given:

A = { x : x ∈ N, 0 < x < 6}

B = {x : x is a prime natural number, 0 < x < 10}

A = { x : x ∈ N, 0 < x < 6}

A = {1, 2, 3, 4, 5}

B = {x : x is a prime natural number, 0 < x < 10}

B = {2, 3, 5, 7}

A - B = {1, 2, 3, 4, 5} - {2, 3, 5, 7}

= {1, 4}

∴ The value A - B is {1, 4}.

We have to select 2 persons out of 76 for handshakes.

\(\therefore\) Number of handshakes \(={ }^{76} \mathrm{C}_{2}=\frac{76 \times 75}{2 \times 1}\)

= 38 × 75

= 2850

Given,

Radius of the loop, \((r)=1 \mathrm{~km}=1000 \mathrm{~m}\)

Speed of the aircraft, \((v)=900 \mathrm{~km} / \mathrm{h}\)

\(v=900 \times \frac{5}{18} \)

\(v=250 \mathrm{~m/s}\)

Centripetal acceleration \(\mathrm (a_{c})=\frac{\mathrm v^{2}}{r}\)

\(=\frac{(250)^{2}}{1000}\)

\(=\frac{250 \times 250}{1000}=62.5 \mathrm{~m/s}^{2}\)

Acceleration due to gravity, \((\mathrm{g})=9.8 \mathrm{~m/s}^{2}\)

So the ratio:

\(\frac{\mathrm{a}_{\mathrm{c}}}{\mathrm{g}}=\frac{62.5}{9.8}=6.38 \approx 6.4\)

So the ratio of its centripetal acceleration with the acceleration due to gravity is \(6.4\).

The general term in the expansion of \(\left(\mathrm{x}-\frac{1}{\mathrm{x}}\right)^{11}\) is given by,

\(\mathrm{T}_{\mathrm{r}+1}=(-1)^{\mathrm{r}} \times{ }^{11} \mathrm{C}_{\mathrm{r}} \times \mathrm{x}^{11-\mathrm{r}} \times\left(\frac{1}{\mathrm{x}}\right)^{\mathrm{r}}\)

\(=(-1)^{\mathrm{r}} \times{ }^{11} \mathrm{C}_{\mathrm{r}} \times \mathrm{x}^{11-\mathrm{r}} \times \mathrm{x}^{-\mathrm{r}}\)

\(=(-1)^{\mathrm{r}} \times{ }^{11} \mathrm{C}_{\mathrm{r}} \times \mathrm{x}^{11-2 \mathrm{r}}\)

Here, n is 11 (i.e., odd), so there will be two middle terms

\(\frac{1}{2}(\mathrm{n}+1)\) th term \(=6\) th term and \(\frac{1}{2}(\mathrm{n}+3)\) th term \(=7\) th term

\(\therefore \mathrm{T}_{6}=\mathrm{T}_{5+1}=(-1)^{5} \times{ }^{11} \mathrm{C}_{5} \times \mathrm{x}^{11-10}\)

\(=-\frac{11 \times 10 \times 9 \times 8 \times 7}{5 \times 4 \times 3 \times 2 \times 1} \times \mathrm{x}\)

= -462 x

And, \(\mathrm{T}_{7}=\mathrm{T}_{6+1}=(-1)^{6} \times{ }^{11} \mathrm{C}_{6} \times \mathrm{x}^{11-12}\)

\(=\frac{11 \times 10 \times 9 \times 8 \times 7}{5 \times 4 \times 3 \times 2 \times 1} \times \mathrm{x}^{-1}\)

\(= \frac{462}{x}\)

Let the sum of the marks of the rest of the students be \(x\).

Incorrect Mean \(=70\)

\(\frac{x+87}{40}=70\)

\(x+87=2800\)

\(x=2713\)

Correct sum \(=x+\) correct marks

\(S=2713+78=2791\)

Correct Mean \(=\frac{2791}{40}=69.775\)

Given, probability of success \(\frac{2}{3}\) and number of trials is 10.

Consider, the most probable number of successes in 10 trials with probability of success \(\frac{2}{3}\) is n.

Now, \(\mathrm{n}=\frac{2}{3}+\frac{2}{3}+\frac{2}{3}+\ldots\) ( 10 times)

\(\mathrm{n}=\frac{2}{3} \times 10\)

\(\Rightarrow \mathrm{n}=6.67\)

\(\Rightarrow \mathrm{n}=7\)

The most probable number of successes in 10 trials with probability of success \(\frac{2}{3}\) is 7.

We have been given the polar coordinates of the vertices of a triangle are \((0,0),\left(3, \frac{\pi}{2}\right)\) and \(\left(3, \frac{\pi}{6}\right)\).

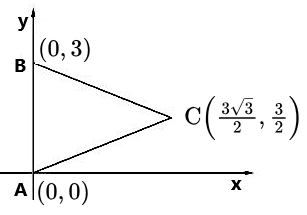
Let us suppose a \(\Delta A B C\) where \(A(0,0), B\left(3, \frac{\pi}{2}\right)\) and \(C\left(3, \frac{\pi}{6}\right)\).

We know that in Cartesian form the polar coordinates \((r, \theta)\) is written as:

\(x\) coordinates \(=r \cos \theta\)

\(y\) coordinates \(=r \sin \theta\)

\(B\left(3, \frac{\pi}{2}\right)\)

\(x\) coordinates \(=3 \cos \frac{\pi}{2}=3 \times 0=0\)

\(y\) coordinates \(=3 \sin \frac{\pi}{2}=3 \times 1=3\)

\(C\left(3, \frac{\pi}{6}\right)\)

\(x\) coordinates \(=3 \cos \frac{\pi}{6}=3 \times \frac{\sqrt{3}}{2}=\frac{3 \sqrt{3}}{2}\)

\(y\) coordinates \(=3 \sin \frac{\pi}{6}=3 \times \frac{1}{2}=\frac{3}{2}\)

We know that distance between two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is given by,

\(D=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

We have \(A(0,0)\) and \(B(0,3)\)

\(\Rightarrow A B=\sqrt{(0-0)^{2}+(3-0)^{2}}\)

\(=\sqrt{0+9}\)

\(=3\)

Also, we have \(A(0,0)\) and \(C\left(\frac{3 \sqrt{3}}{2}, \frac{3}{2}\right)\)

\(\Rightarrow A C=\sqrt{\left(\frac{3 \sqrt{3}}{2}-0\right)^{2}+\left(\frac{3}{2}-0\right)^{2}}\)

\(=\sqrt{\frac{27}{4}+\frac{9}{4}}\)

\(=\sqrt{\frac{36}{4}}\)

\(=\frac{6}{2}\)

\(=3\)

Again, we have \(B(0,3)\) and \(C\left(\frac{3 \sqrt{3}}{2}, \frac{3}{2}\right)\) \(\Rightarrow B C=\sqrt{\left(\frac{3 \sqrt{3}}{2}-0\right)^{2}+\left(\frac{3}{2}-3\right)^{2}}\)

\(=\sqrt{\frac{27}{4}+\left(\frac{-3}{2}\right)^{2}}\)

\(=\sqrt{\frac{27}{4}+\frac{9}{4}}\)

\(=\sqrt{\frac{36}{4}}\)

\(=\frac{6}{2}\)

\(=3\)

So, we get \(A B=B C=A C=3\) unit.

We know that if a triangle has all its sides equal then it must be an equilateral triangle.

Thus, \(\mathrm{ABC}\) is an equilateral triangle.