Arithmetic Progressions Test - 6

S₁₁ = S₁₉
This means that the sum of terms from T₁₂ to T₁₉ is zero; which indicates that out of these 8 terms, half are positive and half are negative with same magnitude. Also, the next 11 terms have the same sum as the first 11 terms are having, but of opposite sign. This will result in the sum of the first 30 terms as 0 (zero).

For an A.P.,
a_n = a + (n - 1)d
47 = 101 + (n - 1)(-2)
n = 28
S_n = (a + )
= 14(101 + 47)
= 2072

T₉ + T₁₄ + T₁₈ = T₂₀ + T₂₄
⇒ 3a + 38d = 2a + 42d
⇒ a = 4d
= =

Given: a = 42°, d = 33°
Sum of all the interior angles of an n-sided polygon is (n - 2)180°.
Therefore, (n - 2)180° = [2a + (n - 1)d]
(n - 2) × 180 = (n/2)(2 × 42 + (n - 1) × 33)
360n - 720 = 84n + 33n² - 33n
11n² - 103n + 240 = 0
(n - 5)(11n - 48) = 0
This implies, n = 5 as sides can't be fraction in number.

Here, a = and T₁₃ = m
Hence, m = + (13 – 1)d
m – = 12d
d =

According to question,
The 17^th term of an A.P. is 2 times its 15^thterm.
a + 16d = 2(a + 14d)
16d - 28d = 2a - a
-12d = a [Equation 1]
T₁₈ = a + (n - 1)d
= a + (18 - 1)d
= a + 17d
= -12d + 17d [From equation 1]
= 5d = 5(6) = 30

The positive integers divisible by 6 are: 6, 12, 18, 24, ….
Here, first term a = 6; common difference d = 12 – 6 = 6
The 85^th term is:
a₈₅ = 6 + (85 – 1) × 6
= 6 + 504 = 510
So, the sum of the first 85 natural numbers is:

S₈₅ = × (a + a₈₅)

= 42.5 × (6 + 510)
= 42.5 × 516 = 21930

Let the consecutive terms be (a - d), a, (a + d).
Sum of these terms = 54
a - d + a + a + d = 54
3a = 54
a = 18
Thus, the numbers will become 18 - d, 18, 27 + 18.
Their product = (18 - d) × 18 × (18 + d)
18² - (d)² =
324 - (d)² = 308
-d² = 308 - 324
(d)² = 16
d = ±4
Let d = 4
The terms are:
18 – 4 = 14; 18; 18 + 4 = 22

Here, S = 126, a = 11 and d = 4
126 =
252 = n[22 + 4n – 4]
= n(4n + 18]
4n² + 18n – 252 = 0

2n² + 9n – 126 = 0
2n² + 21n – 12n – 126 = 0
n(2n + 21) – 6[2n + 21] = 0
(2n + 21)(n – 6) = 0
n = or n = 6
Hence, n = 6

5, 2, –1, –4, …
First term = a
Common difference = d
Sum of n terms = (2a + (n – 1)d)
= (2 5 + (n – 1)(–3))
= (10 + (n – 1)(–3))
= (13 – 3n)

Since a, b, c, d, e and f are in AP.
Let common difference be x.
1^st term = a
2^nd term = b = a + x
3^rd term = c = a + 2x
4^th term = d = a + 3x
5^th term = e = a + 4x
e – c = a + 4x – (a + 2x) = a + 4x – a – 2x = 2x
Also, 2(d – c) = 2(a + 3x – a – 2x) = 2x

Given: =

a + (m - 1)d =

an + mnd - nd = 1 ... (1)



a + (n - 1)d =

am + mnd - md = 1 ... (2)
From (1) and (2), we get
an + mnd - nd = am + mnd - md
a(n - m) - (n - m)d = 0
a = d
Consider (1): an + mnd - nd = 1
dn + mnd - nd = 1

d =

Hence, a =

Sum of mn terms of AP =

=

=

Here, first term, a = 2 … (1)
Fourth term = a + 3d = 6 ... (2)
∴ 2 + 3d = 6
d =
Then, sum = [2a + (n - 1)d]
6800 = [4 + (n - 1)]
6800 = [4 + n - ]
6800 =
6800 2 3 = 8n + 4n²
40,800 = 8n + 4n²
4n² + 8n - 40,800 = 0
n² + 2n - 10,200 = 0
(n + 102)(n - 100) = 0
n = 100 or n = -102 (not possible)
∴ n = 100

If $a is the first installment and the common difference is $d,
Then,
Sum of n terms =
Sum of all installments = S₄₀ = [2a + (40 - 1) d] = total debt = 3,600
2a + 39d = 180 …(1)
Also, S₃₀ = [2a + (30 - 1) d] = of the total debt = 2400.
2a + 29d = 160 …(2)
Subtracting (2) from (1), we get, 10d = 20.
d = 2
a = $51

10 + 12 + 14 + ------- + 200
a = 10, d = 2
T_n = 200 = 10 + (n - 1) × 2
n = 96

S_n =

S_n = [10 + 200] = 48 × 210 = 10,080
Sum of the numbers, which are multiple of 6:
12 + 18 + _ _ _ _ _ + 198
198 = 12 + (m - 1) 6
m = 32
S_m = [12 + 198] = 16 × 210 = 3,360
Required Sum = 10,080 - 3,360 = 6,720

First term a = 13
Let the number of terms be 'n'.
Common difference, d = 5
Sum = 418
418 =
836 = n(26 + 5n - 5)
836 = 5n² + 21n
5n² + 21n - 836 = 0
5n² + 76n - 55n - 836 = 0
n(5n + 76) - 11(5n + 76) = 0
(n - 11)(5n + 76) = 0
n = 11 or
Since, n cannot be negative and a fraction,
Hence, n = 11

Here, a = x, d = y
a_n = z
z = x + (n – 1)y
z – x = ny – y
n =

Let the first term or sale in the 1^st year be a.
Difference = d
Total sales or S₈ of the first 8 years = 1,18,800
Sale in the 10^th year or a₁₀ = 9,900
Sale in the 4^th year or a₄ = ?
i.e.
a₁₀ = a + (10 - 1)d = 9,900
a + 9d = 9900
a = 9900 – 9d --- (1)
As the total sales figure of the first 8 years is given, we can calculate the common difference or the amount of sales decreasing each year.





1,18,800 = 4[2a + 7d]
2a + 7d = 29,700
2(9,900 – 9d) + 7d = 29,700
19,800 – 18d + 7d = 29,700
-11d = 9900
d = -900 (Minus sign implies that the A.P. is getting decreased)

Put d = -900 in equation (1).
a = 9,900 – 9(-900)
= 9,900 + 8,100
= 18,000
So, sale in the 1^st year or a = 18,000
Sale in the 4^th year or a₄ = a + (4 - 1)d
= 18,000 + 3(-900) (a = 18,000, d = -900)
= 18,000 – 2,700
= 15,300 units

Let the first term or the number of admissions in the first year be a.
Difference = d
Total number of admission in n years or S_n = 49,600
Number of admissions in the 4^th year or a₄ = 5400
Number of admissions in the 6^th year or a₆ = 8600
Number of admissions in the n^th year or a_n = ?
a is the first term and d is the common difference.
a + 3d = 5400 --- (1)
a + 5d = 8600 --- (2)
Subtracting equation (1) from equation (2),
d = 1600
Putting d = 1600 in equation (1),
a + 3(1600) = 5400
a = 5400 – 4800
a = 600
Number of admissions in the 1^st year = 600
Total number of admission in n years or S_n = 49,600







n[800n – 200] = 49,600
800n² – 200n – 49,600 = 0

(Dividing the whole equation by 200)
4n² – n – 248 = 0
4n² – 32n + 31n – 248 = 0
(n - 8)(4n + 31) = 0
n = 8, []
⇒ n = 8
Number of admissions in the 8^th year or a_n = a + (n - 1)d
a₈ = a + 7d
a₈ = 600 + 7(1600)
= 11,800

Production of ACs in the first year or a₁ = 10000
Production of ACs in the n^th year or a_n = 2500
Production of ACs is decreasing every year by 1500.
d = -1500

Now,
Production in the n^th year or a_n = a + (n - 1)d
2500 = 10000 + (n - 1)(-1500)
-7500 = -1500n + 1500
1500n = 7500 + 1500
1500n = 9000
n = 6
So, production in the 6^th year = 2500
Total production of ACs in 6 years or S_n =

= 3(12,500) = 37,500

Therefore, total production of ACs in 6 years is 37,500 units.

T₇ = 5400

T₁₁ = 7000

T₇ = a + 6 × d

T₁₁ = T₇ + 4d

7000 = 5400 + 4 × d; d = 400;

T₇ = a + 6 × 400

5400 = a + 2400

a = 3000
Production in 1 year = S₁₂ = (2 × a + 11d) = 6(2 × 3000 + 11 × 400) = 62,400

Let the distance between the hurdles be d m.
Given distance between the first hurdle and the original position or a = 15 m
Number of hurdles or n = 30 m
Total distance to be covered = 9.6 km = 9600 m
As a person has to come back to the starting point after crossing each hurdle, the sum of the distances of all hurdles from the starting point would be half of the distance covered.











Distance of the 30^th hurdle or

305 = 15 + 29d
290 = 29 d
d = 10 m

The hurdles are placed at 10 m from each other.

(i) Given: The first two terms of an A.P. are k and k + 2.
Therefore, a = first terms of the A.P. = k
Difference between the consecutive terms (d) = k + 2 – k = 2
Also, n = number of terms = 11
Now, using formula a_n = a + (n – 1) × d; where a_n is the last term of the series,
a₁₁ = k + (11 – 1) × 2
a₁₁ = k + 20
Hence, (k + 20) is the 11^th term.
Now,
Sum of the first 11 terms,
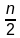
S_n = × (a + a_n)
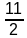
S₁₁ = × (k + k + 20)
S₁₁ = 11 × (k + 10) = 11k + 110_.
Now, using formula a_n = a + (n – 1) × d; where a_n is the last term of the series,
a₇ = k + (7 – 1) × 2
a₇ = k + 12
Hence, (k + 12) is the 7^th term.
Now,
Sum of the first 7 terms:
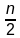
S₇ =× (a + a_n)
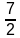
S₇ =× (k + k + 12)
S₇ = 7 × (k + 6) = 7k + 42
Hence, the difference between the sum of the first 11 terms and the sum of the first 7 terms can be calculated as:
S₁₁ – S₇ = 11k + 110 – (7k + 42) = 4k + 68 = 4(k + 17)

(ii) Let 'k' be the number of all terms in the series of both the even and odd numbers.
Therefore,
For odd numbers:
As the first odd number is '1' and the second odd number is '3', the difference between the first and second terms is 2.
a_n = a + (n – 1) × d
a_k = 1 + (k – 1) × 2
a_k = 1 + 2k – 2
a_n = 2k – 1
Now,
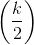
Sum of all the odd terms = × (1 + 2k – 1)
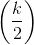
= × 2k
= k² … Eq. 1
Now,
For even numbers:
As the first even number is '0' and the second even number is '2', the difference between the first and second terms is 2.
a_n = a + (n – 1) × d
a_k = 0 + (k – 1) × 2
a_k = 0 + 2k – 2
a_k = 2k – 2
Now,
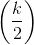
Sum of all the even terms = × (0 + 2k – 2)
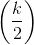
= × (2k – 2)
= k × (k – 1)

= k² - k … Eq. 2

We have to find the difference between the sum of all the odd natural numbers and the sum of all the even natural numbers.
Therefore, using Eq. 1 and Eq. 2,
Difference = k² - (k² - k) = k² - k² = k

(iii) Given series:
(k + 1), (k + 3), …, (k + 13)
As the first and second terms are (k + 1) and (k + 3), the common difference is k + 3 – k – 1 = 2.
So, the series would continue like:
(k + 1), (k + 3), (k + 5), (k + 7), (k + 9), (k + 11) and (k + 13)
Now, the sum of the first 5 terms can be calculated as:
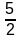
S_{(first five terms)} =× (k + 1 + k + 9)
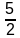
=× (2k + 10)

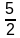
=× 2(k + 5)

= 5k + 25
Now, the sum of the last five terms of the series is :
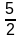
S_{(last five terms)} =× (k + 5 + k + 13)
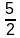
=× (2k + 18)
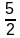
=× 2(k + 9)
= 5k + 45
Now, addition of the sum of the first 5 terms of the series and the sum of last 5 terms of the series = 5k + 25 + 5k + 45 = 10k + 70 = 10(k + 7)

Let 'a' be the first term and 'd' be the common difference of the A.P.
We have,
(1) a₄ - a₂ = 8 ... (1)
(2) a₄ × a₂ = 20 ... (2)
From equation (1), we can say that
(a + 3d) – (a + d) = 8
⇒ 2d = 8
⇒ d = 4 ... (3)
We know that the product of the above mentioned A.P. terms is 20.
So, we need to find two factors of 20 which have a difference of 8.
Factors of 20 = 1, 2, 4, 5, 10, 20
∴ The required two factors are 2 and 10.
⇒ a₂ = 2
And a₄ = 10
If d = 4
⇒ a₁ = a₂ - 4
So, a₁ = -2

T_n = a + (n – 1)d
T₂₅ = -2 + (25 – 1) × 4
T₂₅ = 94

(Using the formula of sum of first n terms of an A.P.)
S_n =

=

= 12.5 × 92
= 1150

(A)
S_n = n/2 [2a + (n -1)d]
S₈ = 8/2 [2a + (8 - 1)d] = 64
2a + 7d = 16 … (1)
Also, S₁₉ = 19/2 [2a + (19 - 1)d] = 361
2a + 18d = 38 ... (2)
Subtracting (1) from (2), we get
11d = 22
d = 2
By putting the value of d in eq. 1,
2a = 16 - 14 = 2
a = 1
Sn = n/2 [2a + (n - 1)d] = n/2 [2 + (n - 1)2]
= 2n + n² - 2n = n²

(B) Let A be the first term and D be the common difference of the A.P.
Then, Sn = an(n - 1)

⇒ [2A + (n - 1)(D)] = an(n - 1)

⇒ 2A + (n - 1)D = 2an - 2a
Compare the coefficient of n and constant term on both sides.
⇒ 2A - D = -2a and D = 2a
⇒ D = 2a
⇒ A = 0
Sum of squares of n terms of the sequence,
S = A² + (A + D)² + (A + 2D)² + ... + (A + (n - 1)D)²
= D²(1² + 2² + 3² + ... + (n - 1)²)

= 4a² = n(n - 1)(2n - 1)

(C) Given:
p^th term = a ⇒ t₁ + (p - 1)d = a … (1)
q^th term = b ⇒ t₁ + (q - 1)d = b ... (2)
r^th term = b ⇒ t₁ + (r - 1)d = c … (3)

The given expression is: a(q - r) + b(r - p) + c(p - q)
This is equivalent to: q(a - c) + r(b - a) + p(c - b)
Putting the values of a, b and c in terms of t₁ and d in the given expression, we get
q[(p - 1)d - (r - 1)d] + r[(q - 1)d - (p - 1)d] + p[(r - 1)d - (q - 1)d]
= q[pd - d - rd + d] + r[qd - d - pd + d] + p[rd - d - qd + d]
= qpd - qrd + rqd - prd + prd - qpd = 0
a(q - r) + b(r - p) + c(p - q) = 0