Mathematics Test - 23

Given:

Mean of 20 observations \(=15\)

Sum of 20 observations \(=15 \times 20=300\)

Correct sum \(=300+8+4-3-6=303\)

\(\therefore\) Correct mean \(=\frac{303}{20}=15.15\)

Given:

\(\sqrt{\frac{1+\cos x}{1-\cos x}}\)

Put \(y=\sqrt{\frac{1+\cos x}{1-\cos x}}\)

Using the double angle formula for cosine function we can write:

\(1+\cos x=2 \cos ^{2} \frac{x}{2}\)

Similarly using the another formula for cosine function we can write:

\(1-\cos x=2 \sin ^{2} \frac{x}{2}\)

Substituting in value of \(y\) we can write:

\(y=\sqrt{\frac{2 \cos ^{2} \frac{x}{2}}{2 \sin ^{2} \frac{x}{2}}}\)

\(=\sqrt{\frac{\cos ^{2} \frac{x}{2}}{\sin ^{2} \frac{x}{2}}}\)

\(=\sqrt{\cot ^{2} \frac{x}{2}}\)

\(=\cot \frac{x}{2}\)

Therefore, \(y=\cot \frac{x}{2}\)

Differentiating both sides with respect to \(\mathrm{x}\):

\(\frac{d y}{d x}=-\frac{1}{2} \operatorname{cosec}^{2} \frac{x}{2}\)

We know that the number of permutations of n dissimilar things, taking r at a time is

${}^n{P}_r=\frac{n!}{\left(n-r\right)!}=n\left(n-1\right)\left(n-2\right).....\left(n-r+1\right)$

There are 7 different letters, i.e. P, I, N, E, A, L, S in the word 'PINEAPPLES'

${}^7{P}_4=\frac{7!}{\left(7-4\right)!}=\frac{7!}{3!}$

=$\frac{7\times 6\times 5\times 4\times 3\times 2\times 1}{3\times 2\times 1}=7\times 6\times 5\times 4=840$

Let, the system of equations be:

\(a_{1} x+b_{1} y+c_{1} z=d_{1}\)

\(a_{2} x+b_{2} y+c_{2} z=d_{2}\)

\(a_{3} x+b_{3} y+c_{3} z=d_{3}\)

\(\left[\begin{array}{lll}a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3}\end{array}\right]\left[\begin{array}{l}x \\ y \\ z\end{array}\right]=\left[\begin{array}{l}d_{1} \\ d_{2} \\ d_{3}\end{array}\right]\) \(=\mathrm{AX}=\mathrm{B}\)

\(X=A^{-1} B=\frac{\operatorname{adj}(A)}{\operatorname{det}(A)} B\)

If \(\operatorname{det}(A) \neq 0\), system is consistent having unique solution.

If \(\operatorname{det}(A)=0\) and \((\operatorname{adj} A) . B=0\), system is consistent, with infinitely many solutions.

If \(\operatorname{det}(A)=0\) and \(( adj A) . B \neq 0\), system is inconsistent (no solution)

Given: The system of equations

\(2 x+y-3 z=5\)

\(3 x-2 y+2 z=5\) and

\(5 x-3 y-z=16\)

So, \(A=\left[\begin{array}{ccc}2 & 1 & -3 \\ 3 & -2 & 2 \\ 5 & -3 & -1\end{array}\right]\)

det \((\mathrm{A})=|\mathrm{A}|=2 \times\{(-2 \times-1)-(-3 \times 2)\}-1 \times\{(3 \times-1)-(2 \times 5)\}+(-3) \times\{(3 \times-3)-(5 \times-2)\}\)

\(\Rightarrow|\mathrm{A}|=2 \times(2+6)-1 \times(-3-10)-3 \times(-9+10)\)

\(\Rightarrow|\mathrm{A}|=16+13-3=26\)

\(\therefore|\mathrm{A}| \neq 0\)

So, system is consistent having unique solution.

Given:

\(\frac{\sin 7 x+6 \sin 5 x+17 \sin 3 x+12 \sin x}{\sin 6 x+5 \sin 4 x+12 \sin 2 x}\)

\(=\frac{\sin 7 x+\sin 5 x+5 \sin 5 x+5 \sin 3 x+12 \sin 3 x+12 \sin x}{\sin 6 x+5 \sin 4 x+12 \sin 2 x}\)

As we know,

\(\sin x+\sin y=2 \sin \left(\frac{x+y}{2}\right) \cos \left(\frac{x-y}{2}\right)\)

\(=\frac{2 \sin 6 x \cos x+10 \sin 4 x \cos x+24 \sin 2 x \cos x}{\sin 6 x+5 \sin 4 x+12 \sin 2 x}\)

\(=\frac{2 \cos x(\sin 6 x+5 \sin 4 x+12 \sin 2 x)}{\sin 6 x+5 \sin 4 x+12 \sin 2 x}\)

\(=2 \cos x\)

In this problem, we need to find the point from the option which does not lie which means the point which does not satisfy the equation of the parabola.

To find the equation of parabola:

From question, the parabola formed with the given vertex and focus on positive x axis is:

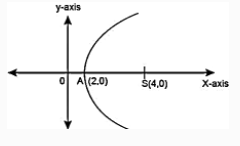
Where,

\({S}=\) Focus

\(A=\) Vertex

The general formula for horizontal parabola is:

\((y-k)^{2}=4 a(x-h)\)

Where,

\((h, k)=\) Vertex

\(a=\) Distance between vertex and focus

Now, from question, we can understand that, \((h, k)=(2,0)\)

Now, ' \(a\) ' is distance between point ' \(A\) ' and 'S'.

The distance between two points is given by the formula:

\(\mathrm{d}=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

On substituting the point ' \(A\) ' and ' \(S\) ',

\(\Rightarrow a=\sqrt{(4-2)^{2}+(0-0)^{2}}\)

\(\Rightarrow a=\sqrt{(2)^{2}}\)

\(\Rightarrow a=\sqrt{4}\)

\(\therefore a=2\)

So, the equation for the given parabola is:

\(\Rightarrow(y-0)^{2}=4 \times 2(x-2)\)

\(\therefore y^{2}=8(x-2)\)

Substituting all the points given in the options:

Option (A):

\((5,2 \sqrt{6}) \Rightarrow({x}, {y})\)

On substituting the point in the obtained parabola equation:

\(\Rightarrow(2 \sqrt{6})^{2}=8(5-2)\)

\(\Rightarrow(4 \times 6)=8(3)\)

\(\Rightarrow 24=24\)

\(\therefore 24-24=0\)

This point satisfies the parabola equation.

Option (B):

\((8,6) \Rightarrow(x, y)\)

On substituting the point in the obtained parabola equation:

\(\Rightarrow(6)^{2}=8(8-2)\)

\(\Rightarrow 36=8(6)\)

\(\therefore 48-36=12\)

This point does not satisfy the parabola equation.

Option (C):

\((6,4 \sqrt{2}) \Rightarrow(x, y)\)

On substituting the point in the obtained parabola equation:

\(\Rightarrow(4 \sqrt{2})^{2}=8(6-2)\)

\(\Rightarrow(16 \times 2)=8(4)\)

\(\Rightarrow 32=32\)

\(\therefore 32-32=0\)

This point satisfies the parabola equation.

Option (D):

\((4,-4) \Rightarrow(x, y)\)

On substituting the point in the obtained parabola equation:

\(\Rightarrow(-4)^{2}=8(4-2)\)

\(\Rightarrow 16=8(2)\)

\(\Rightarrow 16=16\)

\(\therefore 16-16=0\)

This point satisfies the parabola equation.

So, the point which is not satisfying the parabola equation is in option b.

Thus, option (B) does not lie within the parabola.

Probability is the chance of an occurring event.

On tossing a coin, certainty of occurrence of a head \((\mathrm{H})\) or tail \((\mathrm{T})\) on the top.

So, probability of occurrence of head (or tail) \(=\frac{1}{2}\)

Here, a coin tossed repeatedly, but the result of fourth toss is independent of first three tosses.

\(\therefore\) Probability of the tail appearing on the last (fourth) toss \(=\frac{1}{2}\)

\(f: \mathrm{R} \rightarrow \mathrm{R}\) is defincd as \(f(x)=x^{4}\).

Let \(x, y \in \mathrm{R}\) such that \(f(x)=f(y)\).

\(\Rightarrow x^{4}=y^{4}\)

\(\Rightarrow x=\pm y\)

\(\therefore f(x)=f(y)\) does not imply that \(x=y\).

For example \(f(1)=f(-1)=1\)

\(\therefore f\) is not one-one.

Consider an element 2 in co-domain \(\mathrm{R}\). It is clear that there does not exist any \(x\) in domain \(\mathrm{R}\) such that \(f(x)=2\).

\(\therefore f\) is not onto.

Thus, function \(f\) is neither one \(-\) one nor onto.