Chemistry Test - 10

Chloroxylenol, also known as para-chloro-meta-xylenol (PCMX), is an antiseptic and disinfectant which is used for skin disinfection and cleaning surgical instruments.

Main Concept :
Antiseptics and Disinfectants

A chemical substance which has ability to alter the normal body functions of a living organism after injection is called as drug. In medicinal chemistry, a drug can be used for the treatment of diseases caused by microorganism like bacteria, virus, fungi etc.

Generally drugs inhibit the synthesis of cell wall, or cell membrane proteins to prevent the growth of these microorganism or they can be interfere with the processing of nucleic acids of these microorganism to control them. Drugs are complex molecules containing carbon, hydrogen with some heteroatom like oxygen, nitrogen, sulphur.

On the basis of their action of different microorganism and mode of action, drugs can be various types. Some common classes of drugs are as follows.

1.  Antipyretics: These drugs used to reduce fever.

2. Analgesics: They are painkiller which used to reduce pain

3. Antimalarial drugs: These drugs use to treat malaria

4. Antibiotics: They inhibited the germ growth which caused disease

5. Antiseptics: They used to prevention of germ growth near burns, cuts and wounds

Some common natural antiseptics with their applications are as follows:

• Lemon: The presence of citrus juice in lemon make it a good antiseptic which effect on immune function system, circulatory system and digestive systems. Because of its antibacterial nature, it can use to sterilize the air by using few of its drops in a spray bottle.

• Honey: it is a natural antiseptic which used to prevent the infection of wounds due to presence of antibacterial agents which kill the bacteria present in and around the wound. It can also be used for treating ulcers and burns, diarrhea and any vomiting and stomach upsets.

• Pineapple: This fruit is rich in vitamin- A, C, and B, with manganese, which involve in metabolism of proteins and carbohydrates. Bromelain enzyme present in pineapple is used for digesting proteins and enhances medical antibiotics due to its antibacterial properties. Because of antiseptic and astringent nature of pineapple, it can used treatment of pneumonia and infection caused by worms. It is also effective in the treatment of kidney infections and kidney stones.

• Tea Tree Oil: it used for skin disinfectant like acne, athlete's foot and wound healing.

• Lavender: It is a natural antiseptic and astringent which helps with minor skin problems.

• Eucalyptus: It has antiviral and antibacterial properties, thus used for the treatment of flu, throat infections, sinusitis and headaches. Compare to natural antiseptic, synthetic antiseptics are in much more uses due to their reactivity towards bacteria.

Some common examples of synthetic antiseptics are as follow.

1. Alcohols: Some alcohols like ethanol, propanol (1-propanol, 2-propanol) and mixtures of alcohols act as good antiseptics. These alcoholic solutions commonly known as surgical alcohol and used for disinfection of skin before injection along with other antiseptics like tincture of iodine, chlorhexidine etc.

2. Quaternary ammonium compounds: These compounds can act as antibiotic as well as antiseptics also. For example; Benzethonium chloride. These compounds are commonly abbreviated as "Quats," and used to sterilize the skin before surgery as well as for irrigation or as a preservative in eye drops.

3. Boric acid: It's a white crystalline solid, chemically known as orthoboric acid (H₃BO₃). It is mainly used as suppository in the treatment of yeast infections in vagina, in eyewashes. 4. Brilliant Green: It is a triarylmethane dye used as 1% ethanol solution for treatment of small wounds and abscesses.

5. Chlorhexidine Gluconate: It is a biguanidine derivative of chlorhexidine whose alcoholic solution is widely used for skin treatment and for gingivitis.

6. Hydrogen peroxide: The 20 volume solution of hydrogen peroxide acts as good antiseptic due to its oxidising nature and used to clean wounds and ulcers. It also present in many households first aid used to cleanse wounds, disinfect skin, as a gargle or mouthwash.

7. Iodine: The alcoholic solution of iodine is known as tincture of iodine is a good antiseptic used to gentle washing of minor wounds.

8. Octenidine dihydrochloride: It is a bis-(dihydropyridinyl)-decane derivative and a cationic surfactant which show similar in their action to the Quaternary ammonium compounds, but with broader spectrum of activity.

9. Phenolic compounds: Phenol and other phenolic compounds are very common antiseptics used as an antiseptic baby powder, used in mouthwashes and throat lozenges.

10. Other antiseptics: some other antiseptics are polyhexamethylene biguanide (PHMB), Sodium chloride, Sodium hypochlorite, Calcium hypochlorite, Sodium bicarbonate (NaHCO₃) and, Terpenes.

Disinfectants:

Disinfectants are used to kill bacteria. They are used to sterilize instruments, utensils, clothes, floors, sanitary fittings, sputum and excreta. They harm the living tissues and cannot be used on skin. Some examples are phenol, methyl phenol, hydrogen peroxide and sulfur dioxide.

Main Concept :
Examples on Preparation & Properties of Hypo (Sodium thiosulphate)

Sodium thiosulphate

Main Concept :
First law of thermodynamicsThe first law of thermodynamics

The first law of thermodynamics is an application of the law conservation of energy, which states that energy can neither created nor destroyed, that is, the total energy of the system remains constant, though it may change from one from to another. Another statement for the first law arises from the fact that it is impossible to construct a perpetual motion machine that can produce work without spending energy on expenditure of energy.

Derivation

Suppose heat q is supplied to the system with initial internal energy U₁. A part of heat energy is used by the system to do work  ( - w )  while the remaining is used to change the internal energy of the system to U₂. According to the first law of thermodynamics.

ΔU= U₂ - U₁ = q+ w

q = ΔU - ( - w )

So th energy of the system is conserved. For an infinitesimally small change dU in energy, the corresponding changes in heat and work are given by dq and dw and Eq. (2) can be written as:

dU = dq + dw    

For this change in state, q and w will depend on how the change takes place. So these are not state functions. However, the change in internal energy  does not depend on how a change takes place and will depend only on the initial and final states of the system. If there is no transfer of heat to or from the system (q = 0) or no work is done on or by the system (w = 0), then ΔU = 0

Question:

Express the change in internal energy of a system when
(i) No heat is absorbed by the system from the surroundings, but work (w) is done on the system. What type of wall does the system have?
(ii) No work is done on the system, but q amount of heat is taken out from the system and given to the surroundings. What type of wall does the system have?
(iii) w amount of work is done by the system and q amount of heat is supplied to the system. What type of system would it be?

Concept 1 :
Thermodynamic Processes (Isobaric, Isochoric, Isothermal and Adiabatic)

Types of Thermodynamics Process

A thermodynamic process is said to occur when the state of a system changes from one state (initial state) to another (final state).

1. Isothermal process: It is the process carried out at a constant temperature, dT = 0. For this process, the system is usually kept in contact with a constant temperature bath (thermostat) and the constant temperature is maintained by the exchange of heat with the thermostat.

2. Adiabatic process: It is the process in which heat cannot leave or enter the system, dq = 0. For this process, the system is thermally insulated from the surroundings.

3. Isobaric process: It is the process carried out at a constant pressure, dp = 0. All reactions carried out a atmospheric pressure are examples of isobaric process. However, volume change always takes place in an isobaric process.

4. Isochoric process: It is the process in which the volume of the system is kept constant (dV = 0). For example, heating of a substance in a non-expanding chamber.

5. Cyclic process: It is the process in which the initial and final states are indentical.

6. Reversible process: It is the process in which the energy change in each step of the process can be reversed in direction by making a small change in any property of the system, such as temperature, pressure, etc. Two imortant criteria for a process to be reversible are:

(a) The change must be performed at an infinitesimal slow rate.

(b) Threre must be no loss of energy due to friction and no finite temperature differences.

7. Irreversible process: It is the process in which the system or surroundings are not restored to their initial state at the end of the process. All process ocurring spontaneously in nature are irreversible. They always tend to proceed in a definite direction; and do not proceed in the opposite direction without the actions of an external force. Irreversible processes take place spontaneously and not in infinitesimal slow steps that can be reversed. Some examples of irreversible process are expansion and diffusion of gases, flow of heat from a hotter body to a colder body, etc.

Concept 2 :
EnthalpyEnthalpy

Enthalpy is the amount of heat content used or released in a system at constant pressure. Enthalpy is usually expressed as the change in enthalpy. The change in enthalpy is related to a change in internal energy (U) and a change in the volume (V), which is multiplied by the constant pressure of the system.

Enthalpy (H) is the sum of the internal energy (U) and the product of pressure and volume (PV) given by the equation:

H = U + PV

When a process occurs at constant pressure, the heat evolved (either released or absorbed) is equal to the change in enthalpy. Enthalpy is a state function which depends entirely on the state functions T, P and U. Enthalpy is usually expressed as the change in enthalpy (ΔH) for a process between initial and final states:

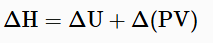
If temperature and pressure remain constant through the process and the work is limited to pressure-volume work, then the enthalpy change is given by the equation:

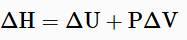
Also at constant pressure the heat flow (q) for the process is equal to the change in enthalpy defined by the equation:

ΔH = q

By looking at whether q is exothermic or endothermic we can determine a relationship between ΔH and q. If the reaction absorbs heat it is endothermic meaning the reaction consumes heat from the surroundings so q > 0 (positive). Therefore, at constant temperature and pressure, by the equation above, if q is positive then ΔH is also positive. And the same goes for if the reaction releases heat, then it is exothermic, meaning the system gives off heat to its surroundings, so q < 0 (negative). If q is negative, then ΔH will also be negative.

Enthalpy Change Accompanying a Change in State of Matter

When a liquid vaporizes the liquid must absorb heat from its surroundings to replace the energy taken by the vaporizing molecules in order for the temperature to remain constant. This heat required to vaporize the liquid is called enthalpy of vaporization (or heat of vaporization). For example, the vaporization of one mole of water the enthalpy is given as:

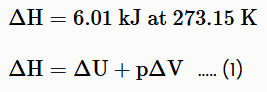
Enthalpy can also be expressed as a molar enthalpy, ΔH_m, by dividing the enthalpy or change in enthalpy by the number of moles. Enthalpy is a state function. This implies that when a system changes from one state to another, the change in enthalpy is independent of the path between two states of a system.

Glycerol (B.P. 290°C ) is separated from spent - lye in the soap industry by distillation under reduced pressure, as for simple distillation very high temperature is required which might decompose the component.

KEY CONCEPTS

Preparation/Separation of Inert gases (i) Dewar's Charcoal adsorption method (ii) Fractional distillation of liquid air

Separation of Noble Gases

The individual noble gases can be separated by Dewar Charcoal adsorption method.

The adsorption capacity power of difference noble gases on charcoal depends on two things:

i. At low temperature the adsorption capacity of these gases increases with the increase in the atomic weight of noble gases.

ii. Adsorption capacity also depends on temperature and it is inversely proportional to the temperature.

Dewar’s Charcoal Adsorption Method

i. Here mixture of inert gases obtained from air, are passed over activated coconut charcoal placed in cold bath at 173K.

ii. Heavier gases like argon, krypton and xenon are adsorbed while lighter gases like helium and neon come out as these are unadsorbed.

iii. When the mixture of He and Ne is passed over activated coconut charcoal at 93K or -180°C , Ne is adsorbed while He comes out. The adsorbed Ne on warming comes out when the temperature of the charcoal is raised.

iv. Now when the charcoal at -100°C on which Ar, Kr and Xe are adsorbed is kept in contact with another charcoal at 77K the lighter Ar diffuses into this charcoal leaving behind Kr and Xe.

v. When the temperature of the charcoal on which Kr and Xe are adsorbed at -100°C or 173K is raised to -90°C or 183K, Kr comes out leaving behind Xe which can be easily collected by heating.

vi. The remaining xenon in adsorbed state comes out on warming.

vii. Here noble gases are separated by fractional distillation of liquid air using the difference in the boiling points of these using Claude’s apparatus.

viii. He and Ne mixed with gaseous N₂

ix. Argon and oxygen in gaseous state above liquid oxygen.

x. Krypton and oxygen in gaseous state above liquid oxygen.

xi. From these fractions inert gases are separated one by one as follows: Separation of He, Ne and N₂

When gaseous mixture of He, Ne and N₂ is passed through a spiral colled by liquid nitrogen most of the nitrogen is removed due to condensation and the remaining nitrogen is removed by passing it over calcium carbide at 1000°C.

i. The remaining mixture having 75% Ne and 25 % He is passed thourgh tubes cooled in liquid hydrogen at 20K, where Ne condenses while He comes out. Separation of Argon and Oxygen.

When the mixture is passed around coils having liquid nitrogen most of the oxygen is removed while remaining oxygen is removed by passing over heated copper.

Seperation of Krypton, Xenon and Oxygen

Krypton, xenon and oxygen an be easily separated by fractional distillation due to wide differences in their boiling points.

Large cation has lesser polarization power whereas small anion is lesser polarisable

KEY CONCEPTS
Conditions of ionic bonding

(i) The atom which changes into cation (+ve ion) should possess 1, 2 or 3 valency electrons. The other atom which changes into anion (–ve ion) should possess 5, 6 or 7 electrons in the valency shell. 

(ii) A high difference of electronegativity (about 2) of the two atoms is necessary for the formation of an electrovalent bond. Electrovalent bond is not possible between similar atoms.

  (iii) There must be overall decrease in energy i.e., energy must be released. For this an atom should have low value of Ionisation potential and the other atom should have high value of electron affinity.
 

(iv) Higher the lattice energy, greater will be the case of forming an ionic compound. The amount of energy released when free ions combine together to form one mole of a crystal is called lattice energy (U).

Examples on Fajan's Rule, Covalent Bond Characteristics

Fajans Rule: The magnitude of polarization or increased covalent character depends upon a number of factors. These factors are,

(1) Small size of cation: Smaller the size of cation, greater is its polarizing power i.e. greater will be the covalent nature of the bond.

(2) Large size of anion: Larger the size of anion, greater is its polarizing power i.e. greater will be the covalent nature of the bond.

(3) Large charge on either of the two ions: As the charge on the ion increases, the electrostatic attraction of the cation for the outer electrons of the anion also increases with the result its ability for forming the covalent bond increases.

(4) Electronic configuration of the cation: For the two ions of the same size and charge, one with a pseudo noble gas configuration (i.e. 18 electrons in the outermost shell) will be more polarizing than a cation with noble gas configuration (i.e., 8 electron in the outer most shell).

For example,

Question: What is the bond character of SnCl₄?

Solution:

Step1: Think about the size of cation and anion

Step2: If the cation is small with large positive charge and large anion

Step3: Then the bond character is covalent.

Sn⁴⁺ is a small cation with high positive charge, and Cl^- is a large anion, as already stated. Therefore, according to the rules, SnCl₄ is the tin halide with more covalent charactor.

Main Concept : 

Test For Iron Sulphate

Iron sulphate on strong heating gives a blackish brown powder and two oxides of sulphur.

2 FeSO ₄ → Fe ₂ O ₃ + SO ₂ + SO ₃

The powder was dissolved in HCl when a yellow solution was obtained which gave blood red coloured solution with thiocyanide ions.

Other Concepts :

Concept 1 :
Examples on Properties of Compounds of Iron

Properties

Carbon monoxide is conveniently produced in the laboratory by the dehydration of formic acid or oxalic acid, for example with concentrated sulphuric acid. Another method is heating an intimate mixture of powdered zinc metal and calcium carbonate, which releases CO and leaves behind zinc oxide and calcium oxide:

Main Concept : 

Faraday's laws electrolysis, First law, Second law

The laws, which govern the deposition of substances (In the form of ions) on electrodes during the process of electrolysis, is called Faraday's laws of electrolysis. These laws given by Michael Faraday in 1833.

(1) Faraday's first law : It states that,

“The mass of any substance deposited or liberated at any electrode is directly proportional to the quantity of electricity passed.”i.e.,

On descending the magnesium group, hydration energies of cations decrease due to increase in size of the ions.

Main Concept :
Solubility of electrovalent compounds

Solubility :Electrovalent compounds are fairly soluble in polar solvents and insoluble in non-polar solvents.  The polar solvents have high values of dielectric constants.* Water, the polar solvent, is one of the best solvents as it has a high value of dielectric constant water is a dipole.  The positive end of the dipole interacts with the negative ion of the electrovalent compound and the negative end of the dipole interacts with the positive ion of the same electrovalent compound as shown in diagram.  Water molecules pull the ions

from the crystal lattice.  These solvated ions lead an independent existence and are thus dissolved in water. The electrovalent compound dissolves in a solvent if the value of solvation energy is higher than the lattice energy of the electrovalent compound.

These ions are surrounded by solvent molecules.  This process is called solvation.  This process is exothermic.

Smaller the ion more of solvation, hence solvation energy will be high.
Other Concepts :

Concept 1 :
Hydration of Ions & Hydration Energy of alkaline earth metals

The hydration enthalpies of group 2 ions are considerably larger than group 1 ions. This is attributed to their smaller ionic sizes and increased charged ion of the alkaline earth metal ions. Like alkali metal ions hydration enthalpies of alkaline earth metal ions decrease with increase in ionic size down the group;

Be²⁺ > Mg²⁺ > Ca²⁺ > Sr²⁺ > Ba²⁺ .

Thus compounds of alkaline earth metals are more extensively hydrated than those of alkali metals e.g. MgCl₂ and CaCl₂ exist as MgCl₂.6H₂O and CaCl₂.6H₂O while NaCl and KCl do not form such hydrates. Further, it is the increase in hydration enthalpy with the ionic charge that is responsible for the existence of group 2 ions exclusively in +2 oxidation state in the aqueous solutions.

Concept 2 :
Solubility of ionic compounds

When a salt is placed in an aqueous medium (i.e. water) a "tug-of-war" immediately begins to take place between the polar water molecules and the ions in the salt. The forces in the tug-of-war are electrostatic and between the ion-ion attractions and the water-ion attractions. If the water-ion attraction wins the war then the salt is soluble. If the ion-ion attractions win then the salt is insoluble. Consider table salt (NaCl), it is highly soluble and its solubility can be written as

At the atomic level, the ions in the salt are "solvated" by the water molecules. The cage of water molecules around the solvated ion is known as a "Hydration" cage.

Introduction, classification, nomenclature and isomerism of alcohols

Introduction of alcohols

The hydroxy derivatives of aliphatic hydrocarbons (compounds having their carbon atoms in chains and not in the form of rings) are called alcohols. When one, two or more hydrogen atoms of a hydrocarbon are replaced by a corresponding number of hydroxyl groups (-OH), alcohols can be obtained.