The interesetion of line and circle is (0, 0) and (2, -2). Now, taking option (c),
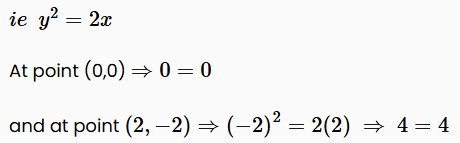
Hence, option (c) is the correct answer
Main Concept :
Equations and Parameters of Standard ParabolaStandard equation of the Parabola:
Consider as S be the focus, ZZ' be the directrix of the parabola and P(x, y) be any point on parabola.
Let AS = AK = a (a > 0) then coordinate of focus S is (a, 0) and the equation of directrix KZ is x = - a or x + a = 0.
If point P (x , y) lies on the parabola then its distance from the focus S and directrix line L must be equal.
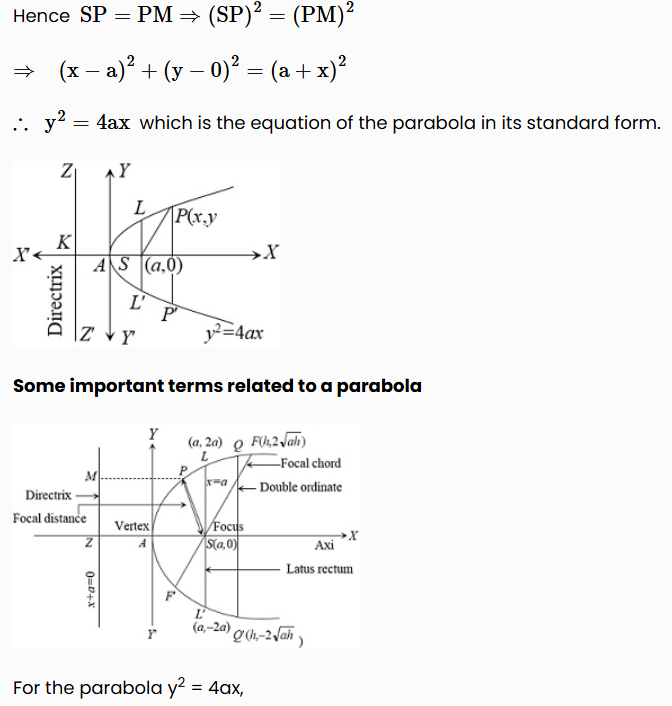
Axis of a parabola: A straight line passes through the focus and perpendicular to the directrix is called the axis of parabola.
For the parabola y2 = 4ax, x - axis is the axis. Here all powers of y are even in y2 = 4ax. Hence parabola y2 = 4ax is symmetrical about x - axis.
We can also generalise this fact that a parabola is always symmetric about its axis.
(2) Vertex : The point of intersection of a parabola and its axis is called the vertex of the parabola.
The vertex is the middle point of the focus and the point of intersection of axis and the directrix. For the parabola y2 = 4ax, A(0, 0) i.e., the origin is the vertex.
(3) Double - ordinate: The chord which is perpendicular to the axis of parabola or parallel to directrix is called double ordinate of the parabola.
Let QQ' be the double - ordinate. If abscissa of Q is h then ordinate of Q, y2 = 4ah or y = 2√ah (for Ist Quadrant) and ordinate of Q' is y = -2√ah (for IVth Quadrant). Hence coordinates of Q and Q' are (h, 2√ah) and (h, -2√ah) respectively.
(4) Latus - rectum: If the double - ordinate passes through the focus of the parabola, then it is called latus - rectum of the parabola.
Coordinates of the extremeties of the latus rectum are L(a, 2a) and L' (a, - 2a) respectively. Since LS = L'S = 2a.
∴ Length of latus rectum LL' = 2(LS) = 2(L'S) = 4a.
(5) Focal Chord: A chord of a parabola which is passing through the focus is called a focal chord of the parabola. Here PP' and LL' are the focal chords.
(6) Focal Distance (Focal length): The focal distance of any point P on the parabola is its distance from the focus S i.e., SP.
Here, Focal distance SP = PM = x + a
Note: If length of any double ordinate of parabola y2 = 4ax is 2l, then coordinates of end points of this double ordinate are
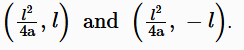


 Get latest Exam Updates
Get latest Exam Updates 
 ×
×
















