Physics Test - 11

Capacitance Capacitance of an Isolated Conductor
When a charge q is given to a conductor it spreads over the outer surface of the conductor. The whole conductor comes to the same potential (say V). This potential V is directly proportional to the charge q, i.e.,

Combination of Capacitors Capacitors in Series and in Parallel

Capacitors are one of the standard components in electronic circuits. Moreover, complicated combinations of capacitors often occur in practical circuits. It is, therefore, useful to have a set of rules for finding the equivalent capacitance of some general arrangement of capacitors. It turns out that we can always find the equivalent capacitance by repeated application of two simple rules. These rules related to capacitors connected in series and in parallel.

Consider two capacitors connected in parallel: i.e., with the positively charged plates connected to a common "input'' wire, and the negatively charged plates attached to a common "output'' wire see Fig. What is the equivalent capacitance between the input and output wires? In this case, the potential difference V across the two capacitors is the same, and is equal to the potential difference between the input and output wires. The total charge Q, however, stored in the two capacitors is divided between the capacitors, since it must distribute itself such that the voltage across the two is the same. Since the capacitors may have different capacitance, C₁ and C₂ the charges Q₁ and Q₂ may also be different. The equivalent capacitance CeqCeq of the pair of capacitors is simply the ratio Q/V, where Q=Q₁+Q₂Q is the total stored charge. It follows that

Consider two capacitors connected in series: i.e., in a line such that the positive plate of one is attached to the negative plate of the other--see Fig. In fact, let us suppose that the positive plate of capacitor 1 is connected to the ``input'' wire, the negative plate of capacitor 1 is connected to the positive plate of capacitor 2, and the negative plate of capacitor 2 is connected to the ``output'' wire. What is the equivalent capacitance between the input and output wires? In this case, it is important to realize that the charge Q stored in the two capacitors is the same. This is most easily seen by considering the "internal'' plates: i.e., the negative plate of capacitor 1, and the positive plate of capacitor 2. These plates are physically disconnected from the rest of the circuit, so the total charge on them must remain constant. Assuming, as seems reasonable, that these plates carry zero charge when zero potential difference is applied across the two capacitors, it follows that in the presence of a non-zero potential difference the charge +Q on the positive plate of capacitor 2 must be balanced by an equal and opposite charge – Q on the negative plate of capacitor 1. Since the negative plate of capacitor 1 carries a charge – Q, the positive plate must carry a charge + Q . Likewise, since the positive plate of capacitor 2 carries a charge + Q, the negative plate must carry a charge – Q . The net result is that both capacitors possess the same stored charge Q. The potential

(v) Capacitance of a conductor do not depend on

(a) Charge on the conductor

(b) Potential of the conductor

(c) Potential energy of the conductor.

Parallel Plate Capacitor

Parallel Plate Capacitor It consists of two parallel metallic plates (may be circular, rectangular, square) separated by a small distance

A transistor oscillator is a amplifier with positive feed back.

A transistor oscillator is the one in which DC supply energy is converted into AC output energy.

KEY CONCEPTS
Positive feedback amplifier oscillator

A transistor amplifier with proper positive feedback can act as an oscillator i.e, it can generate oscillations without any external signal source. Fig. 1 shows a transistor amplifier with positive feedback.



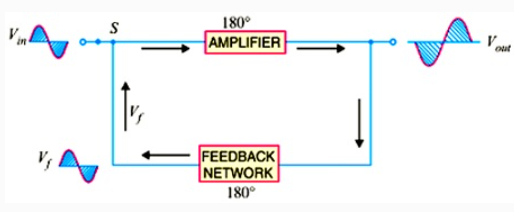
Remember that a positive feedback amplifier is one that produces a feedback voltage $\left(V_f\right)$ that is in phase with the original input signal. As you can see, this condition is met in the circuit shown in fig. A phase shift of is produced by the amplifier and a further phase shift of is introduced by feedback network. Consequently, the signal is shifted by and fed to the input i.e. feedback voltage is in phase with the input signal.

i. We note that the circuit shown in fig. is producing oscillations in the output. However, this circuit has an input signal. This is inconsistent with our definition of an oscillator i.e., an oscillator is a circuit that produces oscillations without any external signal source.

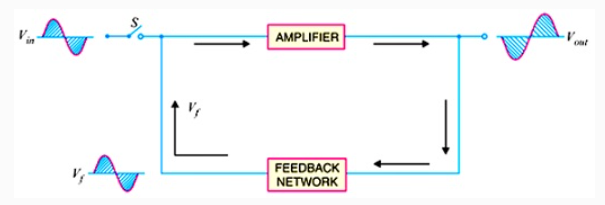
ii. When we open the switch S of Fig. 14.5, we get the circuit shown in Fig. 14.6. This means the input signal. However, Vf (which is in phase with the original signal) is still applied to the input signal. The amplifier will respond to this signal in the same way that it did to V_in  i.e., Vf will be amplified and sent to the output. The feedback network sends a portion of the output back to the input. Therefore, the amplifier receives another input cycle and another output cycle is produced. This process will continue so long as the amplifier is turned on. Therefore, the amplifier will produce sinusoidal output with no external signal source. The following points may be noted carefully: (a) A transistor amplifer with proper positive feedback will work as an oscillator. (b) The circuit needs only a quick trigger signal to start the oscillations. Once the oscillations have started, no external signal source is needed. (c) In order to get continuous undamped output from the circuit, the following condition must be met: AvB = 1 where Av = voltage gain of amplifier without feedback B = feedback fraction This relation is called Barkhausen criterion. Fig. shows the block diagram of an oscillator. Its essential components are:

(i) Tank circuit. It consists of inductance coil (L) connected in parallel with capacitor (C). The frequency of oscillations in the circuit depends upon the values of inductance of the coil and capacitance of the capacitor.

(ii) Transistor amplifier: The transistor amplifier receives d.c. power from the battery and changes it into a.c. power for supplying to the tank circuit. The oscillations occurring in the tank circuit are applied to the input of the transistor amplifier. Because of the amplifying properties of the transistor, we get increased output of these oscillations

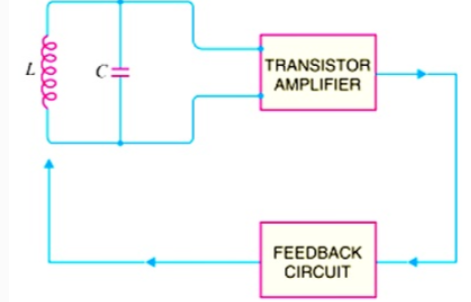
This amplified output of oscillations is due to the d.c. power supplied by the battery. The output of the transistor can be supplied to the tank circuit to meet the losses.

(iii) Feedback circuit: The feedback circuit supplies a part of collector energy to the tank circuit in correct phase to aid the oscillations i.e. it provides positive feedback.

Transistor as an oscillator

(i) The simplest electrical oscillating system consists of an inductance L and a capacitor C connected in parallel.

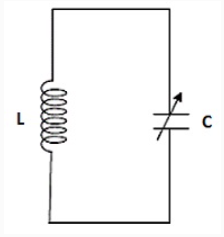
(ii) Once an electrical energy is given to the circuit, this energy oscillates between capacitance (in the form of electrical energy) and inductance (in the form of magnetic energy) with a frequency.

(iii) The amplitude of oscillations is damped due to the presence of inherent resistance in the circuit.

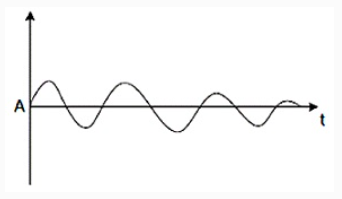
(iv) In order to obtain oscillations of constant amplitude, an arrangement of regenerative or positive feedback from an output circuit to the input circuit is made so that the circuit losses may be compensated.

(v) Circuit diagram of NPN transistor in common emitter configuration as an oscillator.

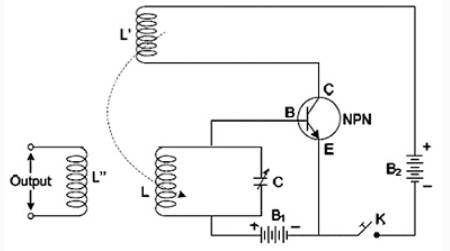
(vi) The tank circuit is used in emitter base circuit of the transistor. The E-B circuit is forward biased whereas the C-B circuit is reverse biased.

(vii) The coil L' in the emitter-collector circuit is inductively coupled with coil L.

(viii) When the key K is closed, I_C begins to increase. The magnetic flux linked with coil L' and hence with L also begins to increase. This supports the forward bias pf B-E circuit. As a result of this I_E increases. Consequently I_C also continues increase till saturation.

(ix) When I_C attains saturation value, mutual inductance has no role to play.

(x) When the capacitor begins to discharge through inductance L, the I_E and hence I_C begins to decrease. Consequently, the magnetic flux linked with L' and hence with L decrease. The forward bias of E-B circuit is opposed thereby further reducing I_E and I_C. This process continues till I_C becomes zero.

(xi) At this stage too, the mutual inductance has once again no role to play.

In a conductor, the electron number density i.e., number of electrons per unit volume of a conductor is very large (≈10²⁸ m^-3), so large current in a conductor is obtained irrespective of their small drift speed.

KEY CONCEPTS

Current#
Current in terms of the drift velocity v_d of the moving charges

i = nqAv_d

n = moving charged particles per unit volume
A = area of cross-section

The current per unit cross-section area is called the current density J.

Current Density
Current density at any point inside a conductor is defined as a vector having magnitude equal to current per unit area surrounding that point. Remember area is normal to the direction of charge flow (or current passes) through that point.

Drift Velocity of Electrons

Drift velocity is the average uniform velocity acquired by free electrons inside a metal by the application of an electric field which is responsible for current through it. Drift velocity is very small it is of the order of 10⁻⁴m/s as compared to thermal speed of electrons at room temperature.

If suppose for a conductor

n= Number of electron per unit volume of the conductor

A= Area of cross-section

V= potential; difference across the conductor

E= electric field inside the conductor

i= current, j=current density, r=specific resitance, s=conductivity then current relates with drift velocity as we can also wirte v_d=i/neA.

Examples on Problems on current density drift velocity of electrons

Find the current flowing inside the conductor. Find the area of cross section of the wire. Ratio of current and area gives the current density.

When a forward bias is applied to a PN junction it applies electric field opposite to potential barrier and hence lowers the potential barrier.

KEY CONCEPTS

pn junction 
A p-n junction is a boundary or interface between two types of semiconductor material, p-type and n-type, inside a single crystal of semiconductor. It is created by doping, for example by ion implantation, diffusion of dopants, or by epitaxy (growing a layer of crystal doped with one type of dopant on top of a layer of crystal doped with another type of dopant). If two separate pieces of material were used, this would introduce a grain boundary between the semiconductors that would severely inhibit its utility by scattering the electrons and holes.

p-n junctions are elementary building blocks of most semiconductor electronic devices such as diodes, transistors, solar cells, LEDs, and integrated circuits; they are the active sites where the electronic action of the device takes place. For example, a common type of transistor, the bipolar junction transistor, consists of two p-n junctions in series, in the form n-p-n or p-n-p.

KEY CONCEPTS

Electric Power

The rate at which electrical energy is dissipated into other forms of energy is called electrical power i.e.

Units: It's S.I. unit is Joule/sec or Watt
Bigger S.I. units are KW, MW and HP, remember 1 HP = 746 Watt

Current
Electric current is nothing but the rate of flow of electric charge through a conductor with respect to time. It is caused by drift of free electrons through a conductor to a particular direction. As we all know, the measuring unit of electric change is Coulomb and the unit of time is second, the measuring unit of current is Coulombs per second and this logical unit of current has a specific name Ampere after the famous French scientist André-Marie Ampere.

As net horizontal force acting on the system is zero, hence momentum must remain conserved. Hence

As per definition,

KEY CONCEPTS

Coefficient of restitution
The coefficient of restitution (COR) of two colliding objects is typically a positive real number between 0.0 and 1.0 representing the ratio of speeds after and before an impact, taken along the line of the impact. Pairs of objects with COR = 1 collide elastically, while objects with COR < 1 collide inelastically. For a COR = 0, the objects effectively "stop" at the collision, not bouncing at all. An object (singular) is often described as having a coefficient of restitution as if it were an intrinsic property without reference to a second object, in this case the definition is assumed to be with respect to collisions with a perfectly rigid and elastic object. The Coefficient of Restitution is equal to the Relative Speed After Collision divided by the Relative Speed Before Collision.

When the ball hits the floor, its gravitational potential energy (=mgh) is at a minimum, as h, height, cannot be any lower (i.e. the ball can't go through the floor), so all its energy is Kinetic. When kinetic energy=0 (i.e. at the peak of its motion when it momentarily stops), all the energy is potential. Thus the ratio of heights (maximum potential energy) is also a square-root ratio one:

Coefficient of restitution

The coefficient of restitution (COR) is a measure of the "bounciness" of a collision between two objects: how much of the kinetic energy remains for the objects to rebound from one another vs. how much is lost as heat, or work done deforming the objects.
The coefficient, e is defined as the ratio of relative speeds after and before an impact, taken along the line of the impact:

This equation shows that in absence of external force for a closed system the linear momentum of individual particles may change but their sum remains unchanged with time.

(2) Law of conservation of linear momentum is independent of frame of reference, though linear momentum depends on frame of reference.

(3) Conservation of linear momentum is equivalent to Newton’s third law of motion.

For a system of two particles in absence of external force, by law of conservation of linear momentum.

These gates form the basis of modern communication through signals as signals get transferred in form of high voltage and low voltage i.e 1 and 0.

Gates are based on semiconductors which is further based on concept of forward biasing and reverse biasing.

S and R are equipotential

KEY CONCEPTS

Equipotential Surfaces#
An equipotential surface is a three dimensional surface on which the electric potential V is the same at every point it. An equipotential surface has the following characteristics.
1. Potential difference between any two points in an equipotential surface is zero.
2. If a test charge q₀ is moved form one point to the other on such a surface, the electric potential energy q₀V remains constant.
3. Nor work is done by the electric force when the test charge is moved along this surface.
4. Two equipotential surfaces can never intersect each other because otherwise the point of intersection will have two potentials which is of course not acceptable.
5. As the work done by electric force is zero when a test charge is moved along the equipotential surface, it follows that $\overrightarrow{\text{E}}$ must be perpendicular to the surface at a every point so that the electric force q₀ $\overrightarrow{\text{E}}$ will always be perpendicular to the displacement of a charge moving on the surface. Thus, field lines and equipotential surfaces are always mutually perpendicular. Some equipotential surfaces are shown in Fig.


The equipotential surfaces are a family of concentric spheres for a point charge or a sphere of charge and are a family of concentric cylinders for a line of charge or cylinder of charge. For a special case of a uniform field, where the field lines are straight, parallel and equally spaced the equipotentials are parallel planes perpendicular to the field lines.

Equipotential Surfaces
Equipotential surfaces are surfaces of constant scalar potential. They are used to visualize an (n)-dimensional scalar potential function in (n-1) dimensional space. The gradient of the potential, denoting the direction of greatest increase, is perpendicular to the surface.

In electrostatics, the work done to move a charge from any point on the equipotential surface to any other point on the equipotential surface is zero because equipotential surfaces are always perpendicular to the net electric field lines passing through it.

KEY CONCEPTS

DISTRIBUTION OF CHARGES ON CONNECTING TWO CHARGED CAPACITOR

When two capacitors are C₁ and C₂ are connected as shown in figure