CBSE 10th Term-2 2022 : Mathematics Important Questions with Their Answers- 4 Marks

Check important answer type questions to prepare for CBSE Class 10th Mathematics Term 2 Exam 2022. The set of questions provided here is best to prepare the 4 marks questions from all chapters of Class 10 Mathematics. These questions have been prepared by the examination experts. Students can easily read all questions in revise them to score maximum marks in their Mathematics exam.

CBSE Class 10 Term 2 Study Material

CBSE Class 10 Term 2 Study Material
CBSE Class 10 Previous Year Question Paper	CBSE Class 10 Sample Paper for Term 2 Exam 2022
CBSE Class 10 Full Study Material for Term 2 Exam 2022 to Score 95+% Marks	NCERT Solutions For Class 10 Maths

Chapter - Quadratic Equations

Q.1 If −5 is a root of the quadratic equation 2x² + px − 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, find the value of k.

Ans : Since −5 is a root of the equation 2x² + px − 15 = 0. Therefore,

2(−5)² − 5p − 15 = 0 ⇒ p = 7

Putting p = 7 in p(x² + x) + k = 0 we get

7x² + 7x + k = 0

Here, a = 7,b = 7;c = k

This equation will have equal roots, if

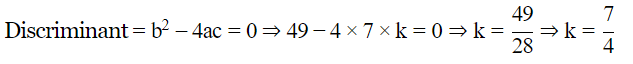
Q.2 Solve the following quadratic equation for x,
4x² + 4bx - (a² - b²) = 0

Ans : Given equation,

4x² + 4bx - (a² - b²) = 0 

⇒ 4x²  +4bx - ( a + b) (a - b) = 0

⇒ 4x² + 2[(a + b) - (a - b)] x - (a + b)(a-b) = 0

⇒ 4x² +2 (a + b)x - 2(a - b)x - (a + b ) (a - b) = 0

⇒ 2x [2x + (a + b)] [(a - b)[2x + (a + b)] = 0

⇒ 2x + (a + b) = 0 or 2x - (a - b) = 0

⇒ x =  - (a + b)/2 OR x = (a - b)/2

Q.3 The sum of the areas of two squares is 468 m². If the difference of their perimeters is 24 m, find the sides of the two squares.

Ans : Let the side of the first square be 'a' m and that of the second square be ′A′ m.

Area of the first square = a² 

Area of the second square = A²

Perimeter of the first square = 4a 

Perimeter of the second square = 4A

Given, difference of their perimeters is 24 m

 4a − 4A = 24

a - A = 6 -------- (1)

Also given, sum of the areas of two squares is 468 m²

a² + A² = 468 ------------ (2)

From (1), a = A + 6

Substituting the value of 'a' in (2), we get

(A + 6)² + A² = 468

=> A² + 12A + 36 + A² = 468              (By using the algebraic identity (a + b)² = a² + 2ab + b²)

=> 2A² + 12A + 36 = 468

=> A² + 6A + 18 = 234                       (By taking 2 as a common factor)

=> A² + 6A − 216 = 0

=> A² + 18A − 12A − 216 = 0             (By splitting the middle term)

=> A (A + 18) - 12 (A + 18) = 0

=> (A + 18) (A - 12) = 0

Thus, A = 12, -18

Since, length cannot be negative, neglect A = -18

Hence, A = 12

Substitute A = 12 in (1)

=> a - A = 6

=> a - 12 = 6

=> a = 18

Therefore, the sides of the first square and the second square whose sum of the areas is 468 m² and the difference of their perimeters is 24m, is 18m and 12m respectively

Q.4 A train travels 180 km at a uniform speed. If the speed had been 9 km/ hour more, it would have taken 1 hour less for the same journey. Find the speed of the train.

Ans : Let the speed of the train be xkmph

The time taken by the train to travel 180km is 180/x h

The increased speed is x + 9

The time taken is 180/x+9

According to the question,

The time taken is 180/x - 1

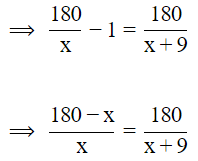
⟹ 180x − x² + 1680 − 9x = 180x

⟹ x² + 9x − 1680 = 0

⟹ x² + 45x−36x−1680=0

⟹ x(x + 45) − 36(x + 45) = 0

x = 36, −45

Speed cannot be negative (In this case,)

So The speed of the train is 36kmph

Q.5 In a flight of 600 km, an aircraft was slowed due to bad weather. Its average speedfor the trip was reduced by 200 km/hr and the time of flight increased by 30 minutes. Find the original duration of the flight.

Ans : Let the original speed of the aircraft be x km/hr. 

Then new speed =(x−200) km.hr

Q.6 The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.

Ans : We have,

Let the large number is = x

Square of smaller number is = 8x

Now, According to given question,

x² − 8x = 180

⇒ x² − 8x − 180 = 0

⇒ x² − (18 − 10)x − 180 = 0

⇒x² − 18x + 10x − 180 = 0

⇒ x(x − 18) + 10(x − 18) = 0

⇒ (x − 18)(x + 10) = 0

⇒ x − 18 = 0, x + 10 = 0

⇒ x = 18, x = −10

⇒ x = −10, 18

Either

x = −10 and x = 18

x = 18 is true (Positive value)

Now, square of small number

= 18x = 18 × 8 = 144

√144

= 12

Hence, this is the answer.

Q.7 The sum of reciprocals of Rehman’s ages (in years) 3 years ago and 5 years from now is 1/3. Find his present age.

Ans : Let Rehman's present age be x yrs.

Therefore his age 3 years ago was (x−3) years.

And his age 5 years from now will be (x+5) years.

Hence applying the above condition, we get

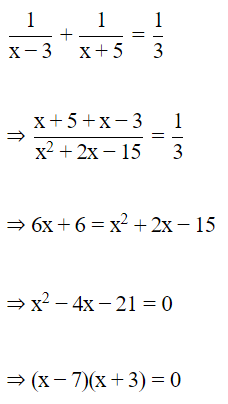
Now, age cannot be negative.

Hence, x = 7

Therefore, the present age is 7 years.

Q.8 A motor boat whose speed is 24 km/h in still water takes 1 hour more to go 32km upstream than to return downstream to the same spot. Find the speed of the stream.

Ans : Given that:

Total Distance = 32km
Speed in Still Water = 24km/h
Let the speed of the stream be ‘x’ km/h
then, Speed moving upstream = 24-x
Speed moving downstream = 24+x

Now for upstream journey

Time taken = 32/ 24-x hours

For downstream journey

Time taken = 32/ 24+x hours

Difference between timings =1 hr
Time of upstream journey = Time of downstream journey +1 hr

Hence the equation becomes

(32/ 24-x) – (32/ 24+x) = 1

1/32= (1/ 24-x) – (1/ 24+x)

1/32= (24+x-24+x) / 242- x²

242- X² = 64X

X2 + 64x – 576= 0

On factorising we get

x² +72x – 8x – 576 = 0

x(x+72) -8(x+72)=0

(X-8)(x=72)=0

x=8 or x=-72

Speed cannot be negative

Hence X=8

Therefore, the speed of the stream is 8 km/hr

Q.9 The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.

Ans : 

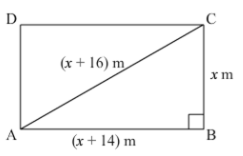
Let the shorter side of the rectangular field be x m.

Then, diagonal of the rectangular field = ( x+ 16) m

Also, longer side of the rectangular field = (x +14) m

In right ΔABC

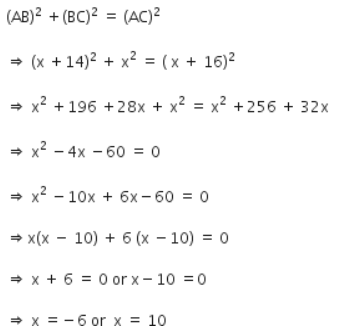
Since length cannot be negative, so x = 10

therefore, the length of the shorter side = 10 m

Length of the diagonal = 10 +16 = 26m

Length of the longer side = 10 +14 = 24

Hence, the length of the sides of the rectangular field is 10 m and 24 m.

Q.10 Solve the following quadratic equation for x: 9x² – 6b²x – (a⁴ – b⁴) = 0

Ans : For the given quadratic equation 9x²−6b²x−(a⁴−b⁴)=0, discriminant is calculated by 

D = (−6b²)² − 4 × 9 × [−(a4 − b4)]

= 36b⁴ + 36(a⁴ − b⁴)

= 36a⁴

Using the quadratic formula, we get

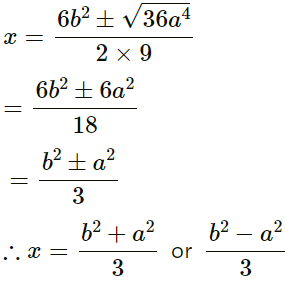
Chapter - Arithmetic Progressions

Q.1 In an A. P. if S₅ + S₇ = 167 and S₁₀ = 235, then find the A.P., where S_n denotes the sum of the first n terms.

Ans : 

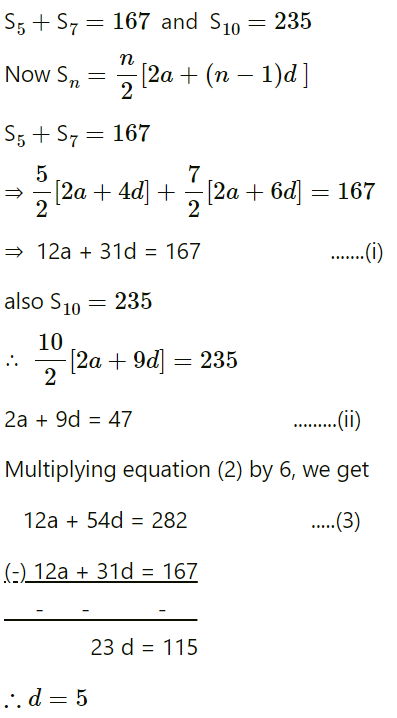
Substituting value of d in (2), we have
2a + 9(5) = 47
2a + 45 = 47
2a = 2
a = 1
Thus, the given A.P. is 1, 6, 11, 16 ,..........

Q.2 The first and the last term of A.P. are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference.

Ans : Let n be the total number of terms and d be the common difference.

Given:

first term = a = 5

last term = l = 45

Sum of all terms = S_n = 400

S_n = n/2[a + l]

400 = n/2[5 + 45]

n/2 = 400/50

n = 16

There are 16 terms in the AP.

Therefore, 45 is the 16th term of the AP.

45 = a + (16 – 1)d

45 = 5 + 15d

40 = 15d

15d = 40

d = 8/3

Common difference = d = 8/3

Q.3 The sum of 3^rd and 7^th terms of an A.P. is 6 and their product is 8. Find the sum of the first 20 terms of the A.P

Ans : a₃ + a₇ = 6; a₃ x a₇ = 8

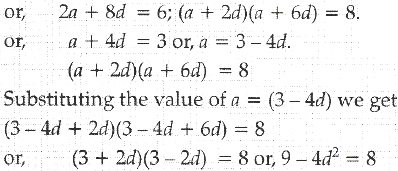
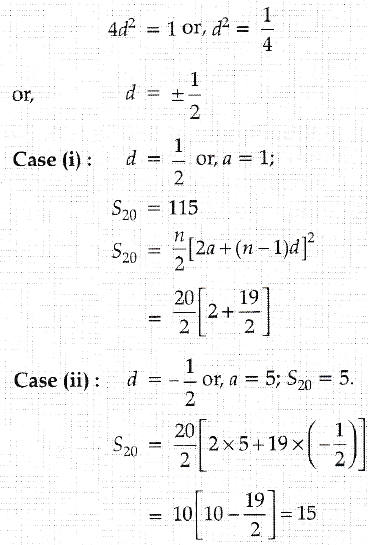
Q.4 If 1 + 4 + 7 + 10 ……. + x = 287 find the value of x

Ans : Given, a = 1, d = 3.

Let number of terms in the series be n.

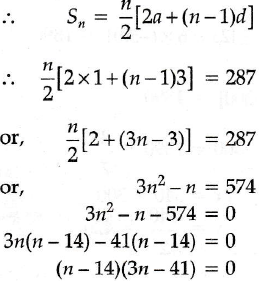
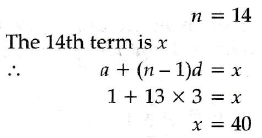
Q.5 The ratio of the sums of first m and first n terms of an A.P.is m2∶n 2. Show that the ratio of its mth and the nth terms is (2m-1): (2n - 1).

Ans : Let the first term and the common difference of the AP be a and d, respectively.

Therefore,

Sum of the first m terms of the AP,

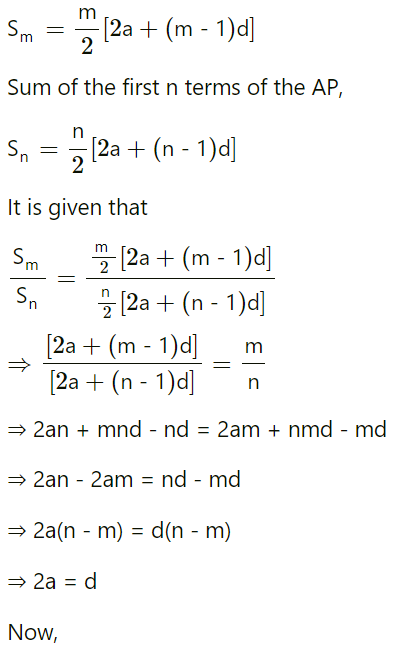
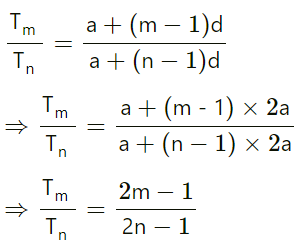
Hence, the ratio of the mth term to the nth term is (2m − 1) : (2n − 1).

Q.6 If the ratio of the 11^th term of an A.P. to its 18^th term is 2 :3, find the ratio of the sum of the first five term to the sum of the first 10 terms.

Ans : 

Q.7 If the p^th term of an A.P. is 1/q and the q^th term is 1/p, prove that sum of the first pq terms of the A.P. is [(pq+1)/2].

Ans : Let first term and common difference of given A.P. be a and d respectively.

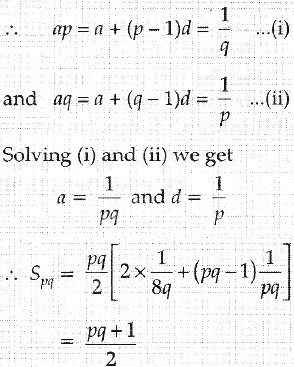
Q.8 The sum of first n terms of an A.P are S1, S2, S3 respectively. The first term of A.P. is 1 and common differences are 1,2 and 3 respectively. Prove that S₁ + S₃ = 2S₂

Ans : 

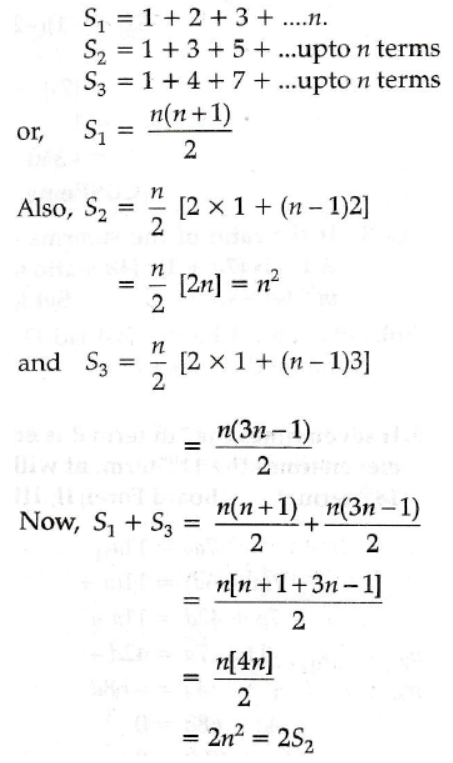
Q.9 If p^th, q^th and r^th terms of an A.P. are a, b, c respectively, then show that (a – b)r +(b – c)p+ (c – a)q = 0

Ans : Let A = first term of the AP.
and
Let d = common difference of the AP

Now
a = A+(p-1).d.......(1)
b = A+(q-1).d.......(2)
c = A+(r-1).d........(3)

Subtracting 2nd from 1st , 3rd from 2nd and 1st from 3rd we get

a-b = (p-q).d......(4)
b-c = (q-r).d........(5)
c-a = (r-p).d.......(6)

multiply 4,5,6 by c,a,b respectively we have

c.(a-b) = c.(p-q).d......(4)
a.(b-c) = a.(q-r).d........(5)
b.(c-a) = b.(r-p).d.......(6)

a(q-r).d+b(r-p).d+c(p-q).d = 0(a(q-r)+b(r-p)+c(p-q)).d = 0

Now since d is common difference it should be non zero

Hence

a(q - r) + b(r - p) + c(p - q) = 0

Q.10 The first and the last terms of an AP are 8 and 350 respectively. If its common difference is 9, how many terms are there and what is their sum?

Ans : First term, a = 8

Common difference, d = 9 

Let the n^th term be the last term.

∴ l = a_n = 350

⇒ a + (n − 1) d = 350

⇒ 8 + (n − 1) × 9 = 350

⇒ (n − 1) × 9 = 342

Chapter - Circles

Q.1 Prove that the lengths of tangents drawn from an external point to a circle are equal.

Ans : Let AP and BP be the two tangents to the circle with centre O.

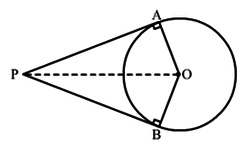
To Prove : AP = BP
Proof :
In ΔAOP and ΔBOP
OA = OB (radii of the same circle)
∠OAP = ∠OBP=90^∘ (since tangent at any point of a circle is perpendicular to the radius through the point of contact)
OP = OP (common)
∴ ΔAOP ≅ ΔBOP (by R.H.S. congruence criterion)
∴ AP = BP (corresponding parts of congruent triangles)
Hence the length of the tangents drawn from an external point to a circle are equal.

Q.2 In fig, two equal circles with centres O and O’, touch each other at X. OO’ produced meet the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of DO’/CO.

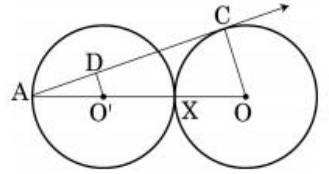
Ans : 

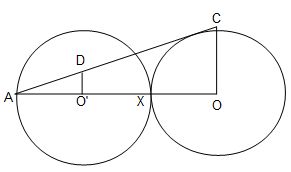
we know that ∠ADO′ = 90° ( since O'D is perpendicular to AC)

∠ACO′ = 90° ( OC(radius)perpendicular to AC(tangent))

In triangles ADO'and ACO ,

∠ADO′ = ∠ACO′ ( each 90°)

∠DAO′ = ∠CAO (common)

by AA criterion ,triangles ADO' and ACO are similar to each other.

AO′AO = DO′CO

(corresponding sides of similar triangles)

AO = AO' + O'X + OX

= 3AO' (since AO'=O'X=OX because radii of the two circles are equal)

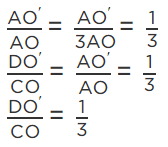
Q.3 The radius of the in-circle of a triangle is 4 cm and the segments into which one side is divided by the point of contact are 6 cm and 8 cm. Determine the other two sides of the triangle.

Ans : BF = BD = 6cm
[length of tangent from external point are equal]

CE = CD = 8cm
[length of tangent from external point are equal]

Let AF = AE = x
[length of tangent from external point are equal]

Now,

Area of ΔABC = Area o fΔAOB + Area of ΔBOC + Area of ΔCOA

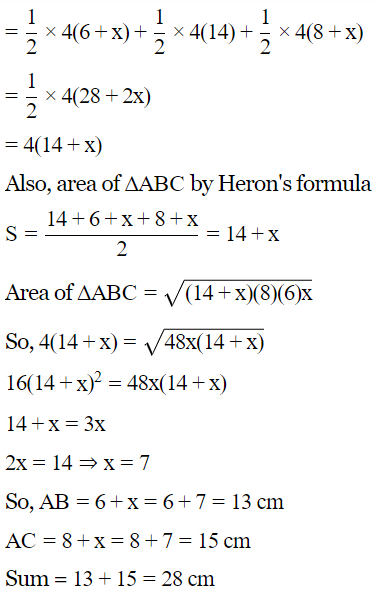
Q.4 In fig, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.

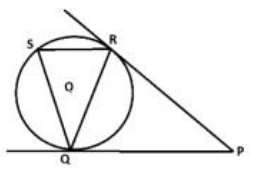
Ans : Given, RS∥PQ and ∠RPQ = 30°

PR = PQ (equal tangents)

∠PRQ = ∠PQR (angle opposite to equal sides)

In △PQR

Q.5 Prove that opposites sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Ans : Given : A circle with centre O touches the sides AB, BC, CD and DA of a quadrilateral ABCD at the points P, Q, R and S respectively.
To prove : ∠AOB + ∠COD = 180°
∠AOD + ∠BOC = 180°

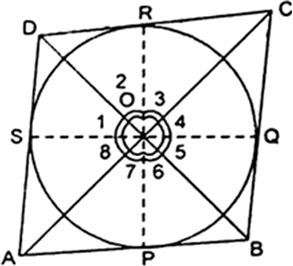
Const. : Join OP, OQ, OR and OS.
Proof : Since, the two tangents drawn from an external point to a circle subtend equal angles at the centre.
∴ ∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6, ∠7 = ∠8
Since sum of all the angles subtended at a point is 360°.
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8
= 360°
⇒ 2 ∠2 + 2 ∠3 + 2 ∠6 + 2 ∠7) = 360°
⇒ 2 (∠2 + ∠3 + ∠6 + ∠7) = 360°
⇒ ∠2 + ∠3 + ∠6 + ∠7) = 180°
⇒ (∠6 + ∠7) + (∠2 + ∠3) = 180°
⇒ ∠AOB + ∠COD = 180°
Similarly, we can prove ∠AOD + ∠BOC = 180°

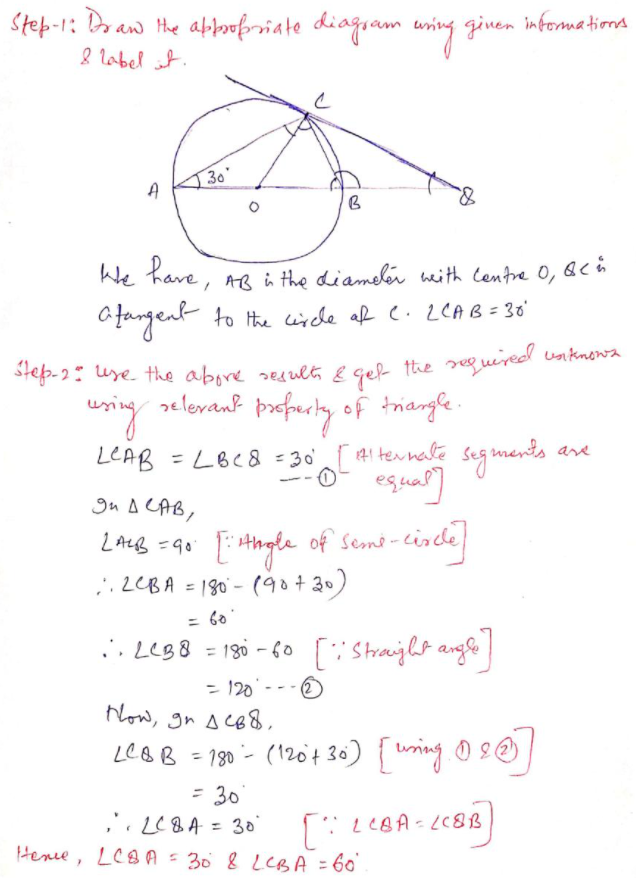
Q.6 . In fig AB is diameter of a circle with centre O and QC is a tangent to the circle at C. If ∠CAB = 30°, find ∠CQA and ∠CBA.

Ans : 

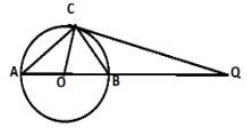
Q.7 In fig, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13cm and OT intersect circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

Ans : 

Thus, AB = 6.6cm

Chapter - Some Application of Trigonometry

Q.1 The angle of elevation of a cloud from a point 100 meter above the surface of a lake is 30° and the angle of depression of its image in the lake is 60° then height of the cloud above the lake is

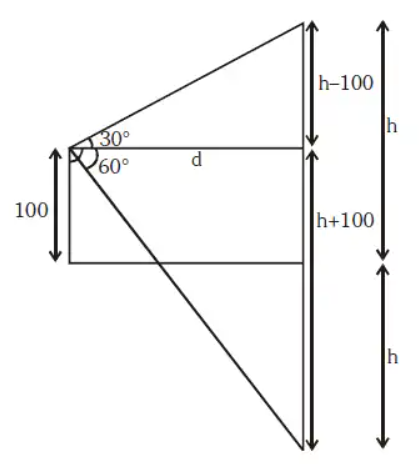
Ans : 

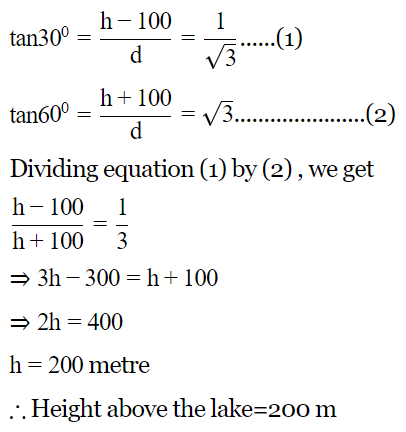
Q.2 From the top of a tower 60m high, the angles of depression of the top and bottom of a vertical lamp post are observed to be 30° and 60° respectively. Find:

a) The horizontal distance between the tower and the lamp post.

b) The height of the lamp post.

c) the difference between the heights of the building and the lamp post.

Ans : 

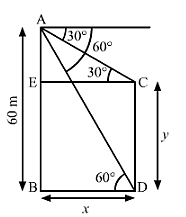
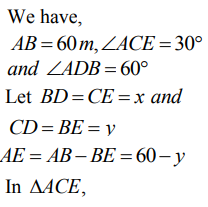
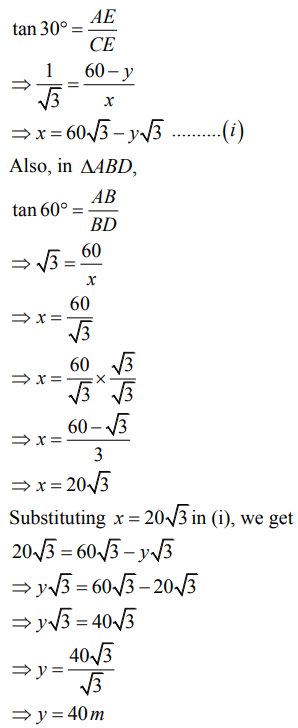
(i) The horizontal distance between AB and CD = BD = x

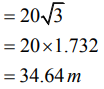
(ii) The height of the lamp post CD =y = 40 m  

(iii) the difference between the heights of the building and the lamp post 

= AB - CD = 60 - 40 = 20 m

Q.3 From a point on a cricket ground, the angle of elevation of the top of a tower is found to be 30° at a distance of 225m from the tower. On walking 150 m towards the tower, again the angle of elevation is found. Find the new angle of elevation and the height of the tower?

Ans : 

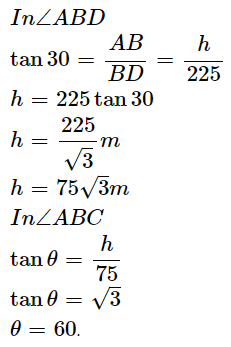
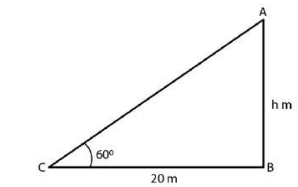
Q.4 A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top the tower is 60°. What is the height of the tower?

Ans : 

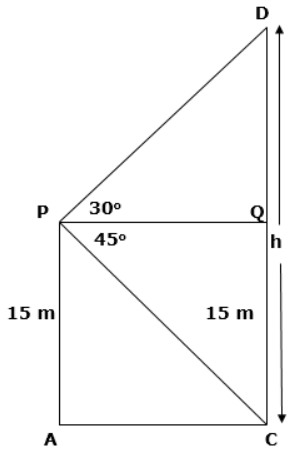
Q.5 From a window 15 metres high above the ground in a street, the angles of elevation and depression of the top and foot of another house on the opposite side of the street are 30° and 45° respectively. Show that the height of the opposite house is 23.65 m. (Use √3 = 1.73)

Ans : 

Chapter - Surface Areas and Volumes

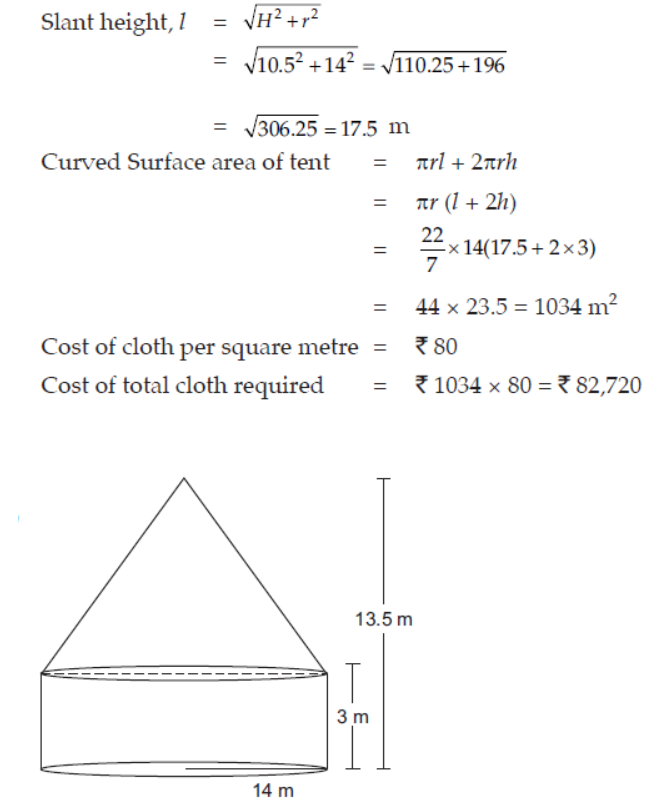
Q.1 A tent is in the shape of a right circular cylinder up to a height of 3 m and conical above it. The total height of the tent is 13.5 m and radius of its base is 14 m. Find the cost of cloth required to make the tent at the rate of ` 80 per square metre. (Take π = 22/7).

Ans : Here, Height of cylindrical part, h = 3m

Height of conical part, H = 13.5 – 3 = 10.5 m

Radius, r = 14 m

Q.2 A hemispherical bowl of internal diameter 36 m contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.

Ans : 

Since 10% liquid is wasted, therefore only 90% liquid is filled into 72 cylindrical bottles.

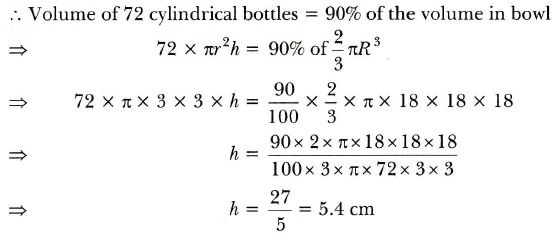
Q.3 From a cuboidal solid metallic block of dimensions 15cm X 10cm X 5cm a cylindrical hole of diameter 7m is drilled out. Find the surface area of the remaining block. (π= 22/7)

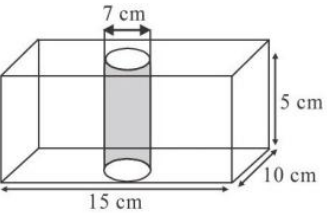
Ans : Total surface area = 2( lb + bh + hl ) + 2πrh

Q.4 A metallic cylinder has radius 3cm and height 5cm. To reduce its weight a conical hole is drilled in the cylinder. The conical hole has a radius of 3/2cm and its depth is 8/9cm. calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.

Ans : 

Hence, Volume of metal left : Volume of metal cut off = 133:2

Q.5 A hollow cylindrical pipe is made up of copper. It is 21 dm long. The outer and inner diameters of the pipe are 10cm and 6cm respectively. Find the volume of copper used in making the pipe. (π= 22/7)

Ans : We have,

Length of cylinder = 21 dm = 210 cm

Outer diameter = 10 cm

Outer radius, R = 10/2 = 5cm

Inner diameter = 6 cm

Inner radius, r = 6/2 = 3cm

∴ Volume of copper used in making the pipe = π (R² – r²)h

= 22/7 (5² – 3²) 210

= 22/7 (25-9) 210

= 10560 cm³

Q.6 A farmer connects a pipe of internal diameter 20cm. from a canal into a cylindrical tank which is 10m in diameter and 2cm deep. If the water flows through the pipe at the rate of 4km per hour, in how much time will the Tank be filled completely?

Ans : We have,

so, the tank will be completely filled in 1 hour 15 minutes.

Q.7 A solid is in the shape of a cone mounted on a hemisphere of same base radius. If the curved surface areas of the hemispherical part and the conical part are equal, then find the ratio of the radius and the height of the conical part.

Ans : We have,

Surface area of Hemisphere = Surface Area of Cone

Let the radius of hemisphere = r

And let the slant length of Cone = l

But according to given question,

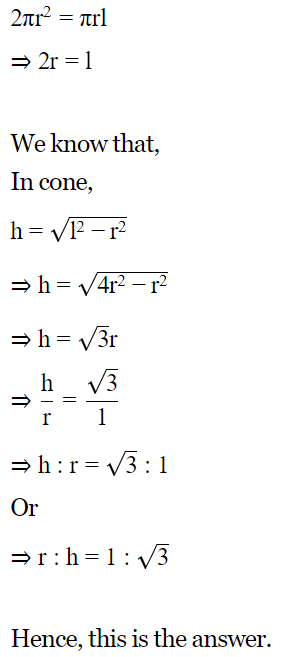
Q.8 A hollow sphere of internal and external diameter 4cm and 8cm respectively is melted to form a cone of base diameter 8cm. find the height and the slant height of the cone.

Ans : Given,

Internal diameter of hollow sphere = 4 cm

So, the internal radius of hollow sphere = 2 cm

External diameter of hollow sphere = 8 cm

So, the external radius of hollow sphere = 4 cm

We know that,

Volume of the hollow sphere 4/3 π × (4³ – 2³) … (i)

Also given,

Diameter of the cone = 8 cm

So, the radius of the cone = 4 cm

Let the height of the cone be x cm

Volume of the cone 1/3 π × 4² × h ….. (ii)

As the volume of the hollow sphere and cone are equal. We can equate equations (i) and (ii)

So, we get

4/3 π × (4³ – 2³) = 1/3 π × 4² × h

4 x (64 – 8) = 16 x h

h = 14

Therefore, the height of the cone so obtained will have a height of 14 cm.

Q.9 A hemispherical tank, full of water is emptied by a pipe at the rate of 25/7 liters/sec. How much time will it, take to empty half of the tank, if the diameter of the base of the tank is 3m?

Ans : 

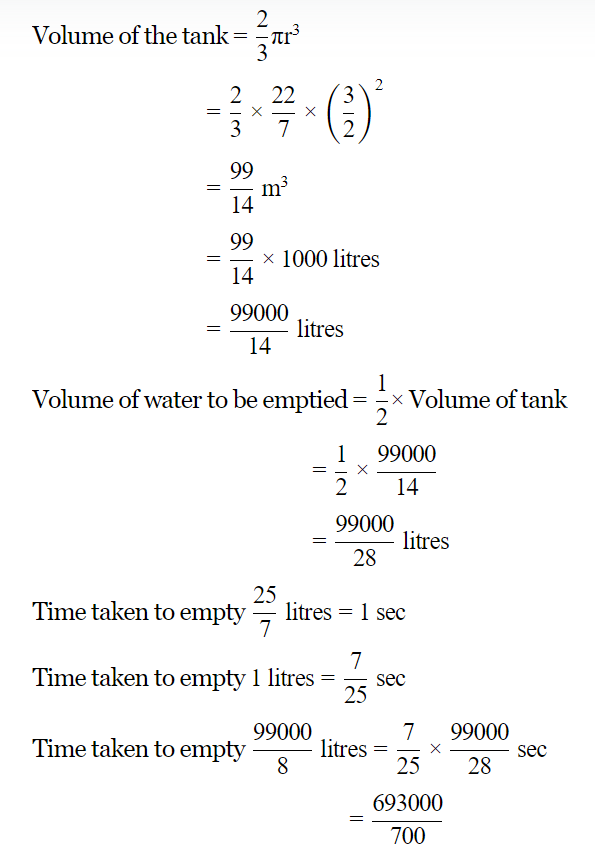
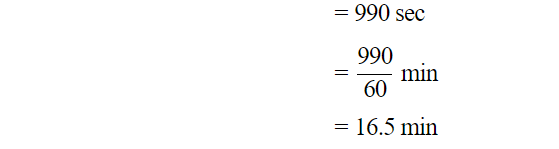
Q.10 Water running in a cylindrical pipe of inner diameter 7cm, is collected in a container at the rate of 192.5 liter per minute. Find the rate of flow of water in the pipe in km/h.

Ans : Diameter of the pipe = 7 cm

radius, r = 7/2 = 3.5

Quantity of water flowing in 1 minute = 192.5 litres

Volume of water flowing in 1 hour = 192.5 × 60 × 1000 cm³−−−−(1)

Also, Volume of water flowing in 1 hour = πr² × rate(R) cm/h−−−−−(2)

From (1) and (2), we get,

πr² × rate(R) cm/h = 192.5 × 60 × 1000 cm³

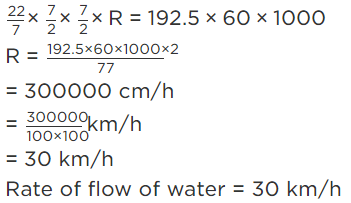
Chapter - Statistics

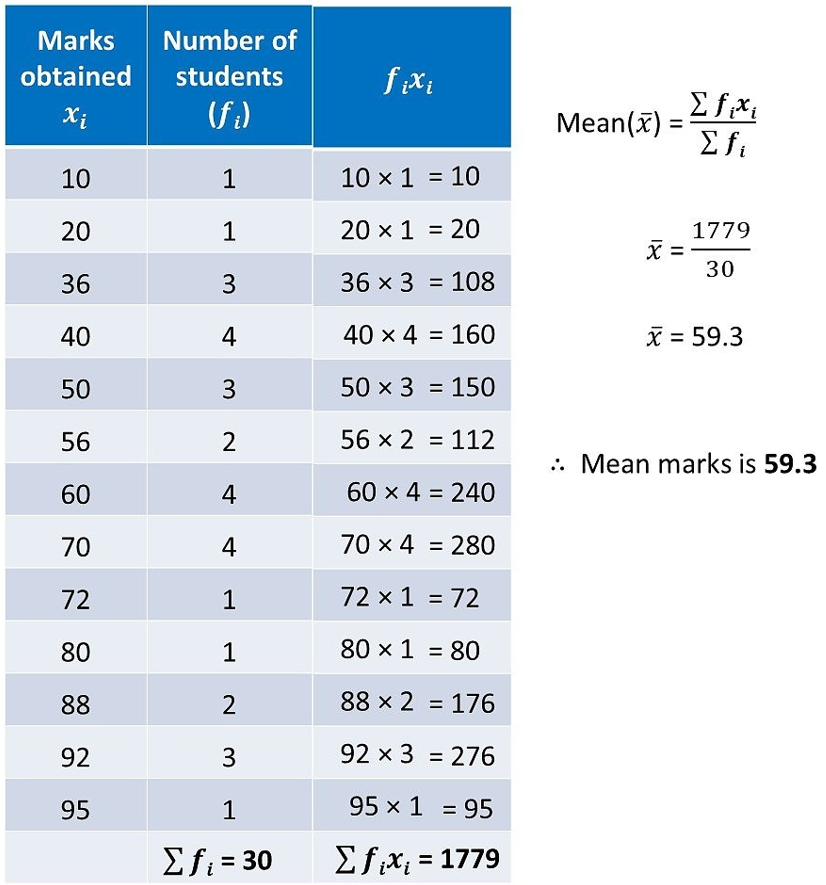
Q.1 The marks obtained by 30 students of class X of a certain school in a mathematics paper consisting of 100 marks are presented in the table below . Find the mean mark.

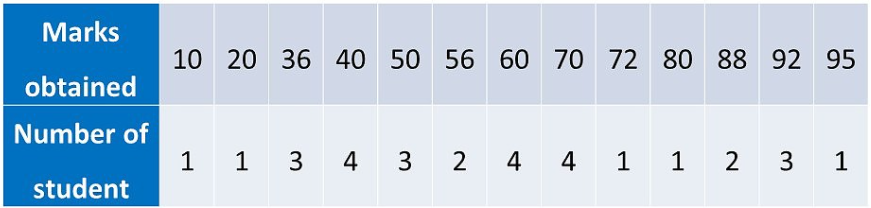
Ans :

Q.2 The following table gives the heights (in cm) of a group of 55 students of a class, Find the modal height of a student.

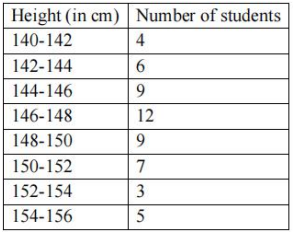
Ans :

Height	No. of students
140-142	4
142-144	6
144-146	9
146-148	12
148-150	9
150-152	7
152-154	3
154-156	5

Modal class is the class with maximum frequency

Maximum frequency = 12

12 lies in 146 - 148

Modal class in 146 - 148 cm

Most of the students height lies between 146 & 148 cm

Mode = 146  + 2 * (12 - 9)/(12 - 9  + 12 - 9)

= 146  + 2 * 3/6

= 146 + 1

= 147

Modal height = 147 cm

Hence maximum number of students have height 147 cm

Q.3 The median of the following data is 525. Find the values of x and y, if the total frequency is 100

Class interval	Frequency
0−100	2
100−200	5
200−300	x
300−400	12
400−500	17
500−600	20
600−700	y
700−800	9
800−900	7
900−1000	4

Ans : Computation of Median

Class interval	Frequency (f)	Cumulative frequency (cf)
0-100	2	2
100-200	5	7
200-300	x	7+x
300-400	12	19+x
400-500	17	36+x
500-600	20	56+x
600-700	y	56+x+y
700-800	9	65+x+y
800-900	7	72+x + y
900-1000	4	76+x + y
		Total = 100

We have,

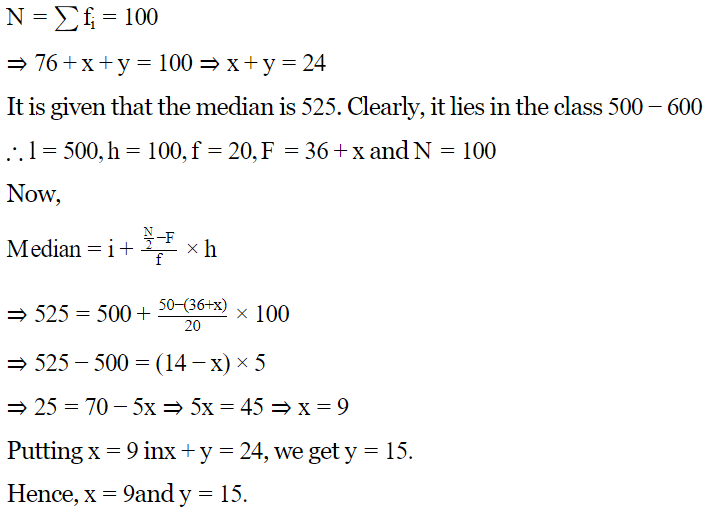
Q.4 The following data gives the information on the observed lifetimes (in hours) of 225 electrical components:

Lifetimes (in hours)	0−20	20−40	40−60	60−80	80−100	100−120
Frequency	10	35	52	61	38	29

Determine the modal lifetimes of the components.

Ans : Here , frequency of class interval 60 − 80 is maximum.

So, it is the modal class

Now, l = Lower limit of modal class = 60

f1​ = Frequency of modal class = 61

f0​ = Frequency of class preceding the modal class = 52

f2 ​= Frequency of class succeeding the modal class = 38

h = Class interval width = 20

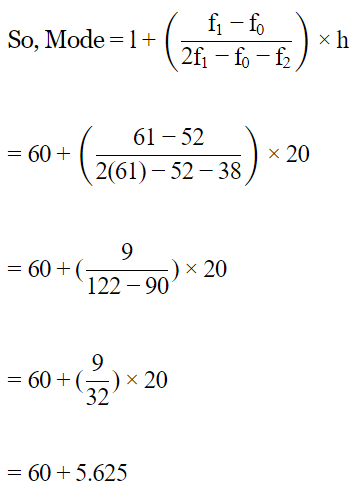
Mode = 65.625

Therefore, modal lifetime of electrical components is 65.625 hours

Q.5 The lengths of 40 leaves of a plant are measured correct to the nearest millimetre and the data obtained is represented in the following table. Find the median length of the leaves.

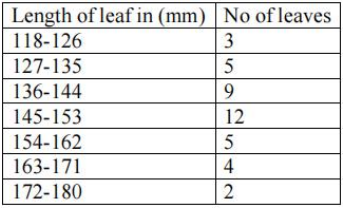
Ans : 

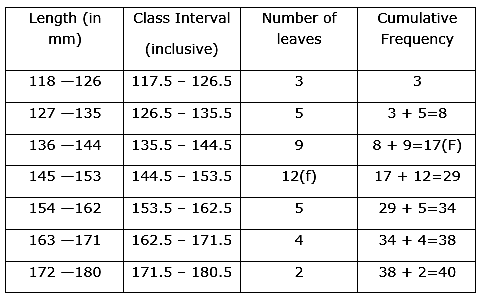
We have n = 40

So, n/2 = 40/2 = 20

The cumulative Frequency just greater than n/2 is 29 then the median class is 144.5 – 153.5 such that

the lower limit (l) = 144.5

cumulative frequency of the class preceding 144.5 – 153.5 (cf) = 17

frequency of the median class 144.5 – 153.5 = 12,

class size (h) = 9

Using the formula,

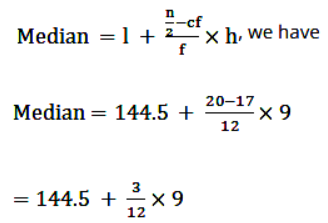
= 144.5 + 2.25

 = 146.75

So, the median length of the leaves is 146.75 mm.