CBSE Class 10th Exam 2025 : Important Chapter-Wise Maths Formulas for Easy Learning

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
Maths is a subject that most students do not like because they don’t understand it well and more likely feel connected with it. If we know all the formulas and techniques to calculate the answer then it will be easy to solve the answer.
It is not difficult to score good marks in maths. However, in maths we get the answer by following the correct steps. So to increase your maths marks and understanding, read this article till the end and you will get all your answers. We make learning maths easy for all students.
Take a look at all the important formulas below, and keep them handy for the 2025 CBSE Class 10 board exam.
CBSE Class 10 Maths Formulas Chapter-Wise
Here is the chapter-wise list given, which you must read to get benefited. Read and revise to become a topper for Class 10 Maths.
Chapter 1 - Real Numbers
|
Natural Numbers |
N ={ 1, 2,3,4,5 … } |
|
Whole Numbers |
W={ 0, 1, 2, 3, 4, 5… } |
|
Rational Numbers |
Those numbers which can be presented in the form of a/b are called Rational Numbers. |
|
Real Numbers |
Real Numbers can be found on a number line |
|
LCM (P, Q, R) |
P.Q.R.H.C.F(P, Q, R) / [HCF ( P, Q) . HCF( Q, R) . HCF ( P, R)] |
|
HCF (P, Q, R) |
P.Q.R.L.C.M(P, Q, R) / [LCM ( P, Q) . LCM ( Q, R) . LCM ( P, R)] |
👉 Read Also- CBSE Board Class 10 Exam 2025 : Subject-wise Most Predicted Questions with Answers; Download Free PDF
Chapter 2 - Polynomials
- (a+b)2 = a2+2ab+b2
- (a−b)2=a2−2ab+b2
- (x+a)(x+b) = x2+(a+b)x+ab
- a2−b2 = (a+b)(a−b)
- a3−b3 = (a−b)(a2+ab+b2)
- a3+b3 = (a+b)(a2−ab+b2)
- (a+b)3 = a3+3a2b+3ab2+b3
- (a−b)3 = a3−3a2b+3ab2−b3
👉 Read Also- CBSE Board Class 10 Exam 2025 : Subject-wise Most Repeated Questions with Answers; Download Free PDF
Chapter 3 - Pair of Linear Equations in Two Variables
- Linear equation in one variable: ax +b =0, a≠0 and a&b are real numbers
- Linear equation in two variables: ax+ by+ c =0 , a≠0 & b≠0 and a,b & c are real numbers
- Linear equation in three variables: ax+ by+ cz= 0, a≠0 , b≠0, c≠0 and a,b,c,d are real numbers
- a1x+b1y+c1=0
- a2x+b2y+c2=0
Where a1, b1, c1, a2, b2, c2 are all real numbers and a12+ b12 ≠ 0, a22+ b22 ≠ 0
Chapter 4 - Quadratic Equations
x = (α, β) = [-b ± √(b2 – 4ac)]/2a provided b2 – 4ac >= 0
A quadratic equation ax2 + bx + c = 0 has
(i) two distinct real roots, if b2 – 4ac > 0,
(ii) two equal roots (i.e., coincident roots), if b2 – 4ac = 0, and
(iii) no real roots, if b2 – 4ac < 0
Chapter 5 - Arithmetic Progressions
The nth term of AP = nth term = a + (n-1) d
Sum of n terms in AP = Sn = n/2[2a + (n − 1) × d]
Sum of all terms in AP with the last term ‘l’ = n/2(a + l)
Chapter 6 - Triangles
Here,
A = Area of Triangle
B = Base of Triangle
H = Height of a Triangle
Area of Triangle = A = ½ (b × h) square units
Area of an Isosceles Triangle = 1/4 b√(4a2 – b2)
Area of a Right Triangle = A = 1/2 × Base × Height
Area of an Equilateral Triangle = A = (√3)/4 × side2
Chapter 7 - Coordinate Geometry
- Distance Formula to find distance between two points P(x1,y1) and Q(x2,y2) is = √[(x2 – x1)2 + (y2 – y1)2 ]
- Distance of a point P(x, y) from the origin is = √x2 + y2
- The coordinates of the point P(x, y) which divides the line segment joining the points A(x1 , y1 ) and B(x2 , y2 ) internally in the ratio m1 : m2 = Section Formula = ((m1x2 + m2x1)/m1+ m2 , (m1y2 + m2y1)/m1+ m2)
- The mid-point of the line segment joining the points P(x1, y1) and Q(x2, y2 ) = [(x1+x2/2), (y1+y2/2)
Chapter 8 - Introduction to Trigonometry
|
Basic Trigonometric Formulas |
|
|
Property |
Mathematical value |
|
sin A |
Perpendicular/Hypotenuse |
|
cos A |
Base/Hypotenuse |
|
tan A |
Perpendicular/Base |
|
cot A |
Base/Perpendicular |
|
cosec A |
Hypotenuse/Perpendicular |
|
sec A |
Hypotenuse/Base |
|
Reciprocal Relations |
|
|
tan A |
sin A/cos A |
|
cot A |
cos A/sin A |
|
cosec A |
1/sin A |
|
sec A |
1/cos A |
Trigonometry Table
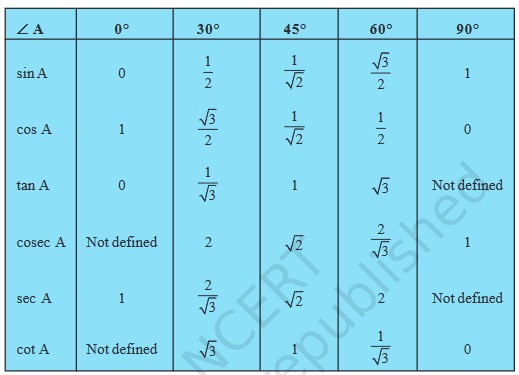
Chapter 9 - Some Applications of Trigonometry
- sin(90°– θ) = cos θ
- cos(90°– θ) = sin θ
- tan(90°– θ) = cot θ
- cot(90°– θ) = tan θ
- sec(90°– θ) = cosecθ
- cosec(90°– θ) = secθ
Chapter 10 - Circles
When r = radius of the circle,
- Circumference of the circle = 2 π r
- Area of the circle = π r2
- Area of a sector of a circle with radius r and angle with degree measure θ = (θ/360) × π r2
- Length of an arc of a sector of a circle with radius r and angle with degree measure θ = (θ/360) × 2 π r
Chapter 11 - Areas Related to Circles
Area of segment of a circle = Area of the corresponding sector – Area of the corresponding triangle.
- The tangent to a circle equation x2 + y2 = a2 for a line y = mx + c is given by the equation y = mx ± a √[1+ m2].
- The tangent to a circle equation x2 + y2 = a2 at (a1,b1) is xa1 + yb1 = a2
Chapter 12 - Surface Areas and Volumes
CUBOID
- Surface Area of a cuboid of length (l), breadth (b), and height (h) = 2 (lb + bh + lh)
- Lateral Surface Area of cuboid = 2 (l + b)h
CUBE
- Surface Area of a cube = 6 ✕ l2 where l is the length
- Lateral Surface Area of cube = 4 ✕ l2, where l is the length
- Volume of cube = l2
CYLINDER
- Total Surface Area of a Cylinder = 2πr (h+r)
- Lateral Surface Area of a Cylinder = 2πrh
- Volume of Cylinder = πr2 h
CONE
- Lateral Surface Area of Cone = πrL
- Total surface area of cone = πr ( L+ r)
- Volume of Cone = ⅓ (πr2 h)
- Volume of a frustum of a cone = 1/3 πh(r₁2 + r₂2 + r₁r₂)
SPHERE
- Surface Area of Sphere= 4 πr2
- Volume of Sphere = 4/3 (πr3)
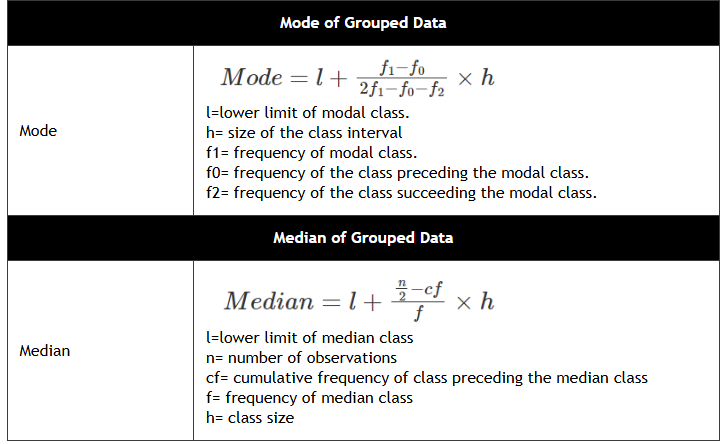
Chapter 13 - Statistics
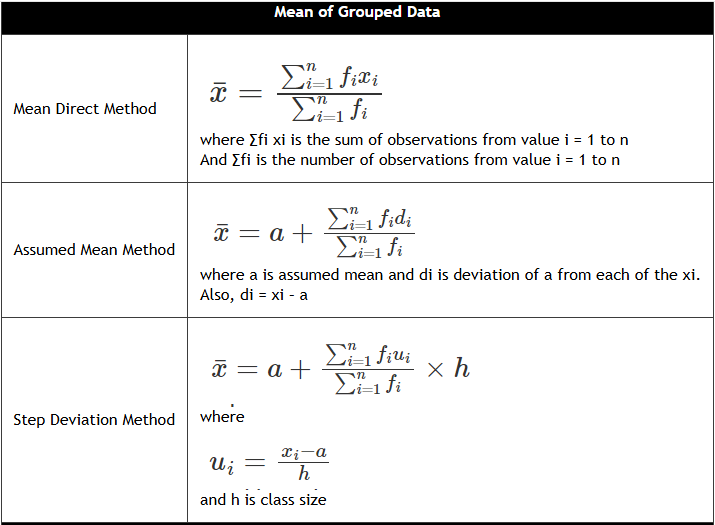
Chapter 14 - Probability
- The theoretical (classical) probability of an event E, written as P(E), is defined as
P (E) = Number of outcomes favourable to E / Number of all possible outcomes of the experiment, where we assume that the outcomes of the experiment are equally likely
- The probability of a sure event (or certain event) is 1
- The probability of an impossible event is 0
- The probability of an event E is a number P(E) such that 0≤ PE≤ 1
-----
👉 Read Also- CBSE Class 10 English Grammar 2025: Most Important Repeated Questions for Board Exam Preparation
👉 Read Also- CBSE Class 10 Board Exam 2024-25 : Most Important English Grammar MCQs, Free PDF Download
👉 Read Also- CBSE Class 10th Hindi Grammar 2025 : Most Repeated Questions from Last 10 Years – Download PDF
👉 Read Also- CBSE Class 10 English 2025: Important Unseen Passages for Board Exam
👉 CBSE Class 10 Study Materials
| CBSE Class 10 Syllabus 2024-25 | NCERT Solutions For Class 10 |
| CBSE Class 10 Previous Year Question Papers | CBSE Class 10 Books |
| CBSE Class 10 Full Study Material | CBSE Class 10 Sample Paper |







 Profile
Profile Signout
Signout













 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










