AEEE Previous Year Question Paper
Using the AEEE previous year question papers available on SelfStudys strategically during your preparation can be very helpful. The Amrita Entrance Examination - Engineering PYQs give you a good idea of how the exam is structured and what questions you can expect. These papers serve as effective tools to enhance your preparation by providing a means to practice and improve your skills.
Solving the AEEE previous year question papers with solutions PDF allows you to analyze your performance and identify key chapters that require more attention. Moreover, they play a crucial role in refining your time management skills, which is an important aspect of success in the exam.
Overview Of Amrita Engineering Entrance Exam
The highlights of this exam are mentioned with all the details in the table below for your reference. You can check them out for a clear understanding of AEEE.
|
HIGHLIGHTS |
DETAILS |
|
Examination Name |
Amrita Entrance Examination - Engineering |
|
Exam Conducting Body |
Amrita Vishwa Vidyapeetham |
|
Frequency of the Exam |
Twice a year |
|
Examination Mode |
Computer-Based Test |
|
Duration to Solve AEEE Exam Question Papers |
2 hours and 30 minutes |
|
Language or Medium of Exam |
English |
|
Number of Sections |
Four
|
|
Total Questions and Marks |
100 Questions and 300 Marks |
|
Campuses Accepting Exam Score |
Amrita University Campuses at:
|
|
Official Website |
AEEE Exam Question Papers In Year-Wise Format
There are a number of AEEE previous year question papers on our digital platform that you can solve. The subject-matter experts at SelfStudys have collected the papers of the past many years from official sources. You can take advantage of these PYPs and increase your question bank significantly to score better marks.
AEEE Previous Year Question Papers With Solutions
The AEEE previous year question papers with solutions PDF can be utilized free of cost on our website. The solutions to each question are created accurately, including detailed and step-by-step explanations. With the help of these solutions, you can cross-check your responses, rectify your mistakes, and learn not to repeat them in the future.
| Year | Solved Papers |
| 2022 | |
| 2019 | |
| 2018 | |
| 2017 | |
| 2015 | |
| 2014 | |
| 2009 |
How To Download The AEEE Previous Year Question Paper From SelfStudys?
To get your hands on the AEEE exam question papers on SelfStudys, you must follow the steps below properly. Just make sure you have a good internet connection to download the PYP.
- The first step is to reach our website which can be done by typing www.selfstudys.com on your favorite web browser.

- Then, you need to move your cursor to the “JEE” section displayed at the header of the homepage.

- Now, you can select the “AEEE Previous Year Paper” from various other exam options.

- Soon, a new page will be loaded on your screen where you will be able to see different year-wise AEEE previous year question papers with solutions.
- You can pick any of the yearly papers and select it to open its PDF file.
- At last, you can click on the download icon to get AEEE previous year question papers saved on your device.

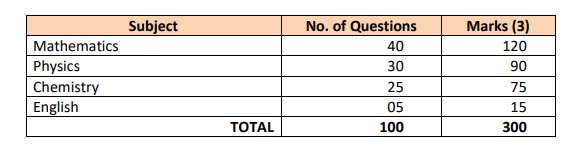
Number of Questions and Marks Distribution For AEEE
With the help of the image below, you can learn about the number of questions in each section of the AEEE exam question papers and their marks distribution.
Syllabus Of AEEE Previous Year Question Papers
As there are various subjects included in the AEEE exam question papers, the syllabus of this exam is quite vast. You can go through the table below to learn which topics are covered in the paper from different subjects.
|
AMRITA ENTRANCE EXAM - ENGINEERING SYLLABUS |
|
|
Mathematics |
|
|
UNIT |
TOPICS |
|
Sets, Relations, and Functions |
Sets and their representation: Union, intersection, and complement of sets and their algebraic properties; Power set; Relation, Type of relations, equivalence relations, functions; one-one, into and onto functions, the composition of functions. |
|
Complex Numbers |
Complex numbers in the form of a+ib and their representation on a plane. Argand diagram. Algebra of complex numbers, Modulus, and argument (or amplitude) of a complex number, square root of a complex number. Cube roots of unity, triangle inequality. |
|
Permutations and Combinations |
Fundamental principle of counting; Permutation as an arrangement and combination as selection, simple applications. |
|
Binomial Theorem |
Binomial theorem for positive integral indices. General and middle terms in binomial expansions, simple applications. |
|
Sequences and Series |
Arithmetic, Geometric, and Harmonic progressions. Insertion of Arithmetic, Geometric, and Harmonic means between two given numbers. Relation between A.M., G.M., and H.M. special series. Arithmetic-Geometric Series, exponential and logarithmic series. |
|
Matrices and Determinants |
Determinants and matrices of order two and three, Properties of determinants. Evaluation of determinants. Addition and multiplication of matrices, adjoint, and inverse of matrix. Solution of simultaneous linear equations using determinants |
|
Quadratic Equations |
Quadratic equations in real and complex number system and their solutions. Relation between roots and coefficients, Nature of roots, Formation of quadratic equations with given roots. |
|
Trigonometry |
Trigonometrical identities and equations. Inverse trigonometric functions and their properties. Properties of triangles including centroid, incentre, circumcentre, and orthocentre, Solution of triangles. Heights and distances. |
|
Measures of Central Tendency and Dispersion |
Calculation of Mean, Median, and Mode of grouped and ungrouped data, Calculation of standard deviation, variance, and mean deviation for grouped and ungrouped data. |
|
Probability |
Probability of an event, addition and multiplication theorems of probability and their applications; Conditional probability; Bayes’ theorem, Probability distribution of a random variate; Binomial and Poisson distributions and their properties. |
|
Differential Calculus |
Polynomials, rational, trigonometric, logarithmic and exponential functions; Graphs of simple functions, Limits, and Continuity; Differentiation of the sum, difference, product and quotient of two functions; Differentiation of trigonometric, inverse trigonometric, logarithmic, exponential, composite and implicit functions; Derivatives of order upto two, Applications of derivatives. |
|
Integral Calculus |
Integral as an anti-derivative. Fundamental integrals involving algebraic, trigonometric, exponential, and logarithmic functions; Integration by substitution, by parts, and by partial fractions; Integration using trigonometric identities; Integral as a limit of sum; Determining areas of the regions bounded by simple curves. |
|
Differential Equations |
Ordinary differential equations, their order, and degree; Formation of the differential equation; Solutions of differential equations by the method of separation of variables; Solution of Homogeneous and linear differential equations of the first order. |
|
Coordinate Geometry |
Review of the Cartesian system of rectangular coordinates in a plane, distance formula, area of triangle, condition for the collinearity of three points, slope of a line, parallel and perpendicular lines, intercepts of a line on the coordinate axes. |
|
The Straight Line and Pair of Straight Lines |
Various forms of equations of a line, intersection of lines, angles between two lines, conditions for concurrence of three lines, and distance of a point from a line. Equations of internal and external bisectors of angles between two lines, equation of family lines passing through the point of intersection of two lines, homogeneous equation of second degree in x and y, angle between pair of lines through the origin, combined equation of the bisectors of the angles between a pair of lines, condition for the general second-degree equation to represent a pair of lines, point of intersections and angles between two lines. |
|
Circles and Family of Circles |
Standard form of the equation of a circle, general form of the equation of a circle, its radius, and center, equation of a circle in parametric form, equation of a circle when the endpoints of a diameter are given, points of intersection of a line and circle with the center at the origin and condition for a line to be tangent, equation of family of circles through the intersection of two circles, condition for two intersecting circles to be orthogonal. |
|
Conic Sections |
Sections of cones, equations of conic sections (parabola, ellipse, and hyperbola) in standard forms, conditions for y=mx+c to be a tangent, and points of tangency. |
|
Vector Algebra |
Vectors and scalars, the addition of two vectors, components of a vector in two dimensions, and three-dimensional space, scalar and vector products, scalar and vector triple product. Applications of vectors to plane geometry. |
|
Three-Dimensional Geometry |
Distance between two points. Direction cosines of a line joining two points. Cartesian and vector equation of a line. Coplanar and skew lines. Shortest distance between two lines. Cartesian and vector equation of a plane. The angle between (i) two lines (ii) two planes (iii) a line and a plane. Distance of a point from a plane. |
|
Physics |
|
|
Units and Dimensions |
Units for measurement, system of units, SI, fundamental and derived units, dimensional analysis. |
|
Kinematics |
Uniform and non-uniform motion, average speed and instantaneous velocity, uniformly accelerated motion, velocity-time, position-time graph. Relative velocity, Motion in a plane, Projectile motion, and Uniform circular motion. |
|
Mechanics |
Motion in one dimension, Newton’s laws of motion, conservation of linear momentum, Friction; Work-Energy theorem, kinetic energy, potential energy; elastic collision in one and two dimensions. Center of mass of a system of particles, center of mass of a rigid body, rotational motion and torque, angular momentum and its conservation, moments of inertia for various geometries, parallel and perpendicular axes theorem. Universal law of gravitation, acceleration due to gravity, planetary motion, Kepler’s law, Satellites. |
|
Solids and Fluids |
|
|
Oscillations and Waves |
|
|
Heat and Thermodynamics |
Heat, work, and temperature; Ideal gas laws; Specific heat capacity, Thermal expansion of solids, liquids, and gases, Relationship between Cp and Cv for gases; Newton’s law of cooling, black body, Kirchoff’s law, Stafan’s law and Wein’s law, thermodynamic equilibrium, internal energy; Zeroth, first and second law of thermodynamics, thermodynamic processes, Carnot cycle, efficiency of heat engines, refrigerator. |
|
Electrostatics, Current Electricity, and Magnetostatics |
|
|
Electromagnetic Induction and Electromagnetic Waves |
|
|
Kinetic Theory of Gases |
Equation of state of a perfect gas, work done on compressing a gas, Kinetic theory of gases - assumptions, the concept of pressure. Kinetic energy and temperature: RMS speed of gas molecules: Degrees of freedom. Law of equipartition of energy, applications to specific heat capacities of gases; Mean free path. Avogadro's number. |
|
Ray and Wave Optics |
|
|
Modern Physics |
|
|
Chemistry |
|
|
Basic Chemical Calculations |
Density- mole concept- empirical and molecular formula- stoichiometry- volumetry, equivalent and molecular masses, percentage composition. |
|
Atomic Structure and Periodicity |
Atomic models, sub-atomic particles, orbital shapes, Pauli’s exclusion, Hund’s rule, Aufbau principle, de-Broglie relation, Heisenberg’s uncertainty, electronic configuration and periodic properties. |
|
Chemical Bonding |
Ionic bonding, lattice energy – Born-haber cycle, covalent bond - Fajan’s Rule –VSEPR theory -- hybridization, valence bond and molecular orbital theory, coordinate, metallic and hydrogen bonding. |
|
S-block and Hydrogen |
Hydrogen, isotopes, liquid hydrogen as fuel, alkali metals, oxides and hydroxides, extraction and properties of lithium, sodium and potassium. Group 2 elements and their properties. |
|
P-block Elements |
Boron - borax, boranes, diboranes, Carbon - allotropes, oxides, carbides, halides and sulfides of carbon group- silicon and silicates – silicones, Nitrogen – Fixation – compounds of nitrogen- Phosphorous – allotropes and compounds. Oxygen - oxides and peroxide. Sulfur – its compounds - inter-halogen compounds. |
|
D and F block Elements |
d-block elements configuration and properties - transition elements, chromium, copper, zinc, silver, interstitial compounds and alloys, f-block elements and extraction, lanthanides and actinides. |
|
Solid State |
Solids - amorphous and crystalline, classification of crystalline - unit cell, Miller indices - packing efficiency, unit cell dimensions, crystal structure, ionic crystals, imperfections in solids, electric and magnetic properties. |
|
Coordination Compounds |
Terminology in coordination- isomerism, Werner, VBT, CFT theories - Bio- coordination compounds. |
|
Gaseous State and Surface Chemistry |
Gaseous state and gas laws, deviation- van der Waal’s constants - Joule-Thomson effect - liquefaction of gases, theory of catalysis, colloids and emulsions. |
|
Colligative Properties |
Lowering of vapor pressure, Depression of freezing point, Elevation in boiling point, Osmotic pressure, abnormality- dissociation and association. |
|
Electrochemistry |
Faraday’s laws - specific, equivalent and molar conductances, Kohlraush’s law and applications- electrode potentials - EMF, electrochemical and, galvanic cells, Nernst equation, batteries, fuel cells, corrosion and its prevention. |
|
Thermodynamics |
First and second law- internal energy, enthalpy, entropy, free energy changes– specific heats at constant pressure and constant volume – enthalpy of combustion, formation and neutralization, Kirchoff law – Hess’s law - bond energy. |
|
Chemical and Ionic Equilibria |
Law of chemical equilibrium, homogenous and heterogeneous equilibrium, Le Chatlier’s principle, equilibrium constants, factors affecting- Ionic equilibrium, ionization of acids and bases, buffer solutions, pH -solubility of sparingly soluble salts. |
|
Chemical Kinetics |
Order, molecularity, rate and rate constant – first and second order reactions - temperature dependence, factors influencing rate of reaction, integrated rate equation, collision theory of chemical reaction. |
|
Basic Organic Chemistry |
Classification, functional groups, nomenclature and isomerism, types of organic reactions, mechanism, purification, qualitative and quantitative analysis carbocation, carbanion and free radical, electron displacement in covalent bond. |
|
English |
|
|
Articles, Synonyms, Antonyms, Preposition, Verbs. |
|
Tips To Solve The AEEE Previous Year Question Paper
Solving AEEE previous year question papers are an integral part of your exam preparation strategy. By following a few tips and techniques, you can approach the papers with confidence and maximize your chances of success. Our team of experts has discussed some of these tips below.
- Familiarize Yourself with the Exam Pattern: Before starting to solve AEEE previous year question papers with solutions PDF, it is important to familiarize yourself with the exam pattern. You should understand the marking scheme, the types of questions asked, and the time allotted for each section. This will give you a clear idea of what to expect and how to approach the paper effectively.
- Start with Easy Questions: When you begin solving AEEE exam question papers, start with the easier questions first. It will help you build your confidence and momentum. As you progress, gradually tackle more challenging questions. You should also remember that time management is key, so don’t get stuck on one question for too long.
- Analyze Mistakes: After solving AEEE previous year question papers with solutions, take the time to analyze your mistakes. You must identify the areas where you struggled and understand why. This will help you pinpoint your weaknesses and focus your efforts on improving them. You may keep a log of your mistakes and revisit them regularly to track your progress.
- Practice Regularly: Consistent practice is essential when preparing for any exam, and AEEE is no exception. You should set aside dedicated time each day to solve AEEE previous year question papers and other practice materials. The more you practice, the more familiar you will become with the exam pattern and the better prepared you will be on exam day.
- Time Management: Time management is crucial during the real exam, and it's equally important when solving AEEE previous year question papers with solutions PDF. You must practice solving these PYPs within the allotted time to simulate exam conditions. You can use techniques like skipping difficult questions and coming back to them later to optimize your time.
- Seek Help When Needed: If you encounter questions or concepts in AEEE exam question papers that you are struggling with, don’t hesitate to seek help. You should reach out to teachers, mentors, or online resources for clarification. You can also join study groups or forums where you can discuss doubts and learn from others’ experiences.
- Revision: Regular revision is essential to reinforce your learning and solidify concepts. You should review AEEE previous year question papers with solutions periodically to keep your skills sharp. Focus on areas where you are weak and strive to improve with each revision.
- Stay Positive: Finally, you must maintain a positive mindset throughout your preparation journey. You should believe in your abilities and stay motivated, even when faced with challenges. Celebrate your progress and milestones along the way, and don’t be too hard on yourself for setbacks. With determination and perseverance, you can conquer AEEE previous year question papers and excel in the exam.
Engineering Courses Offered After AEEE
We have gathered information regarding several engineering courses that are offered based on the Amrita Entrance Exam - Engineering score at different campuses of this University. You can have a look at the table below for details.
|
BACHELOR OF TECHNOLOGY COURSES |
LOCATION OF AMRITA VISHWA VIDYAPEETHAM CAMPUS |
|
Mechanical Engineering |
Courses offered in:
|
|
Computer Science and Engineering |
Courses offered in:
|
|
Electronics and Communication Engineering |
Courses offered in:
|
|
Electrical and Electronics Engineering |
Courses offered in:
|
|
Civil Engineering |
Courses offered in:
|
|
Chemical Engineering |
Courses offered in:
|
|
Aerospace Engineering |
Courses offered in:
|
|
Electronics and Computer Engineering |
Courses offered in:
|
|
Electrical and Computer Engineering |
Courses offered in:
|
|
Computer and Communication Engineering |
Courses offered in:
|
|
Computer Science and Engineering (Cyber Security) |
Courses offered in:
|
|
Computer Science and Engineering (Artificial Intelligence) |
Courses offered in:
|
|
Automation and Robotics Engineering |
Courses offered in:
|
|
Robotics and Artificial Intelligence (RAI) |
Courses offered in:
|
|
Artificial Intelligence and Data Science |
Courses offered in:
|
Cities For Amrita Entrance Exam - Engineering
There are several cities where you are permitted to take the AEEE exam question papers. You can check out the images below for the list of different exam centers where AEEE is conducted.
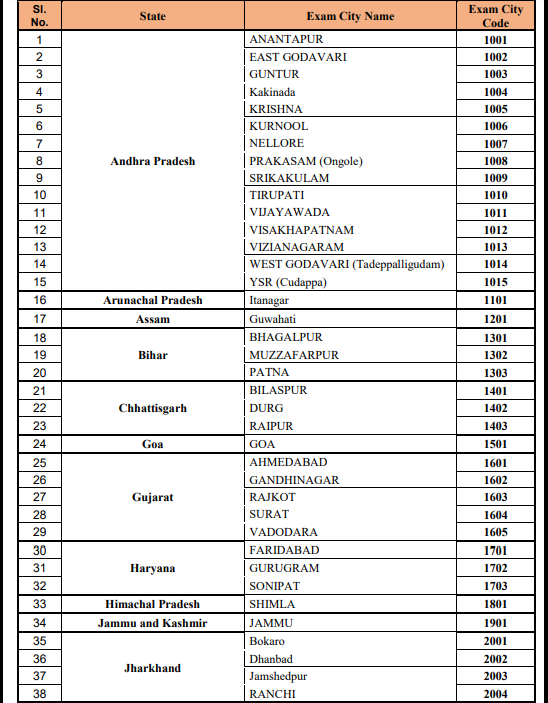
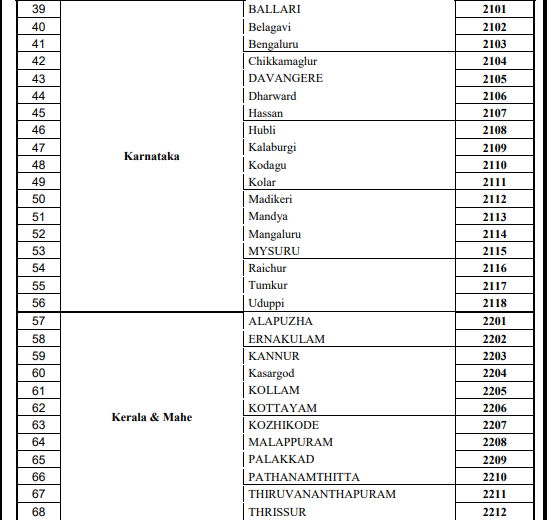
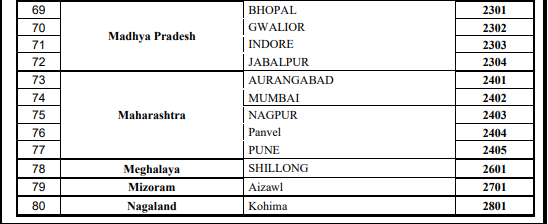
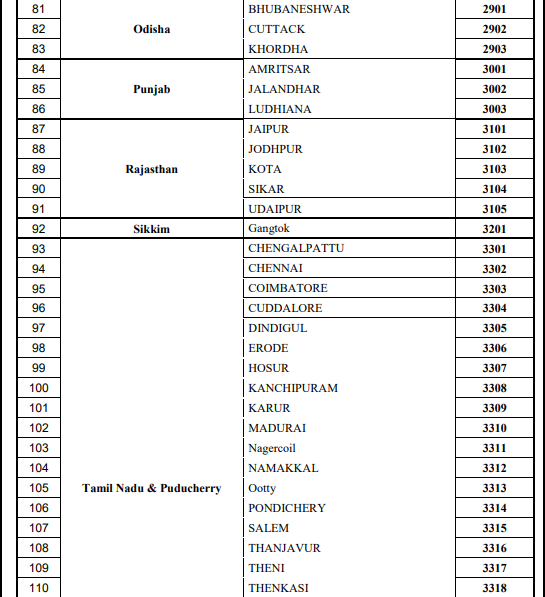

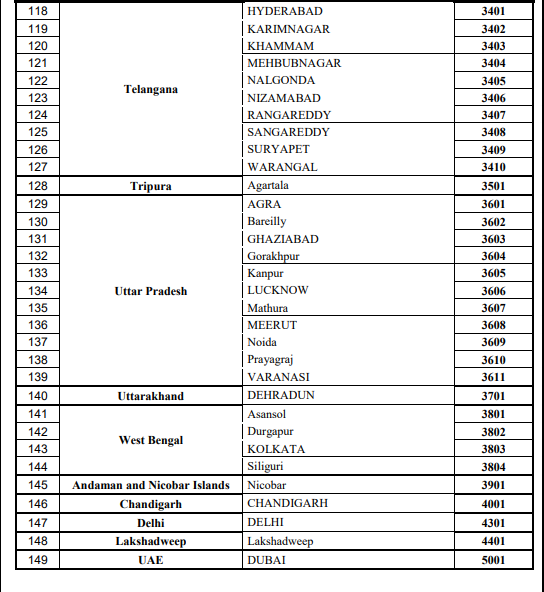
While AEEE previous year question papers with solutions are a valuable tool, consistent practice, a strong understanding of concepts, and thorough revision are very important for guaranteed success.







 Profile
Profile Signout
Signout










 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










