Given,
Richard earned a total of 22.5 points and he was not the first in any level. The only way he can win 22.5 points without being first in any level is if he earned 7.5 in two levels, 5 in one level and 2.5 in another level.
From (2), Connor and Poppy did not win the highest points in the game.
From (6), Sarah also did not win the highest points in the game.
From (4), one of the persons was the first in two levels and this person did not win the highest points. This person must have earned a minimum of 10 + 10 + 2.5 + 2.5 = 25 points in the game. The person who earned the highest points must have earned more than this. From this, we can infer that Richard also cannot be the person who earned the highest points.
Hence, only Mason can be the person who earned the highest points.
From (5), Mason was the first in one level. He is not the third in any level. Also, Richard was the second in two levels (since he earned 7.5 in two levels). Hence, the maximum points that Mason can win = 10 + 7.5 + 7.5 + 2.5 = 27.5 points.
Since Mason has to win more than 25 points, he must have earned 27.5 points. The person who was first in two levels must have earned 25 points (this is the only way for him to have earned less points than Mason).
From (2) and (6), Poppy and Sarah cannot be the person who earned 25 points.
Hence, Connor must be the person who earned 25 points. This is possible if he was the first in two levels and fourth/fifth in two other levels.
From (2), Poppy must have earned 20 points. This is possible only if Poppy was the first in one level, the third in another level and fourth/fifth in two levels (Poppy cannot be the second in any level because Richard and Mason are second in two levels each). The points that Poppy wins in this case = 10 + 5 + 2.5 + 2.5 = 20 points.
Sarah must have been the third in two levels and fourth/fifth in two levels. The total points that Sarah earned = 5 + 5 + 2.5 + 2.5 = 15 points.
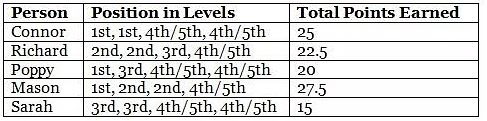
The following table presents the positions of the five persons in the four levels and the total points earned by them in the game.
Connor earned 2.5 points in two levels. In these two levels, Sarah could have got 2.5 points. Hence, we cannot say that Connor definitely earned more than Sarah in at least three levels.
Richard could have earned 2.5 points in the same level that Sarah earned 2.5 points. In the level that Richard earned 5 points, Sarah could have earned only 2.5 points (since two persons could not have earned 5 points). In the other two levels that Richard earned 7.5 points, Sarah would have got less points than Richard. Hence, Richard would have definitely earned higher points than Sarah in three levels. Poppy earned 2.5 points in two levels. In these two levels, Sarah could have earned 2.5 points. Hence, we cannot say that Poppy definitely earned more than Sarah in at least three levels. Mason earned 10 points in one level and 7.5 points in two levels. In all the three levels, Mason would have earned higher points than Sarah. Hence, the given condition is satisfied for two persons, Richard and Mason.


 Get latest Exam Updates
Get latest Exam Updates 
 ×
×
















