Quantitative Aptitude (QA) Test

Result

Quantitative Aptitude (QA) Test - 30

Score
-
out of -
Rank
-
out of -

TIME Taken - -

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Weekly Quiz Competition

Question 1
3 / -1

There were 500 seats in a cinema hall placed in N identical rows. After the renovation of the hall the total number of seats became 450. The number of rows was reduced by 5 but each row contained 5 seats more than before. What were the total number of rows and total number of seats in a row respectively in the hall before the renovation?

A
50 and 10

B
30 and 15

C
25 and 20

D
20 and 25

Solution

Let the number of rows be x and the number of seats per row be y.

Given (xy) = 500...(i)

and (x - 5)(y + 5) = 450...(ii)

From (i) and (ii), (y - x) = 5

Among all the pairs of factors of 500, only 25 and 20 satisfy the above condition.

Hence, option (4) is the correct answer.
Question 2
3 / -1

When five is added to three times a number and the result is squared, the result obtained is four times the square of the sum of the number and its next multiple. What could be the number?

A

B

C

D

Solution
Question 3
3 / -1

A car and a bus start from a same point in the same direction. After T hrs the car is 45km ahead of the bus, while after 9hrs distance between the car and the bus is same as distance covered by the car in one hour. If relative speed of the car and the bus if they move towards each other is 255km/h, then how much distance (in km) can the car cover in

A
337.5

B
320

C
336.3

D
305.2

Solution

Let the speed of the car be x km/h and the speed of the bus be y km/h.

Distance covered by the car in one hour = Distance between the car and the bus in 9hrs

⇒ x = 9(x - y) [therefore, x > y]

⇒ x = 9x - 9y

= 9y = 8x .....(1)

And x + y = 255 ......(2)

From (i) and (ii).

x = 135 and y = 120

After T hrs, the car is 45km ahead of the bus.

(135 - 120)T = 45

Hence, required distance = 2.5 × 135 = 337.5km.
Question 4
3 / -1

The lengths of the sides of the triangle are x, 21, and 40, where x is the shortest side. A possible value of x is

A
18

B
19

C
20

D
17

Solution

Note: Sum of any two sides of the triangle is greater than the third side. As per this rule, x + 21 > 40 and, 21 + 40 > x

From above two inequalities, we get 19 < x < 61.

Hence, a possible value of x can be 20.
Question 5
3 / -1

Bheem, Jaggu and Raju start from Dholakpur at the same time on their cycles to go to Sultanpur. Bheem reaches Sultanpur first and turns back and meets Jaggu at a distance of 9 miles from Sultanpur. When Jaggu reaches Sultanpur, he too turns back and meets Raju at a distance of 7 miles from Sultanpur. If 3 times the speed with which Bheem cycles at a speed which is equal to 5 times Raju’s speed, what could be the distance (in miles) between the points Dholakpur and Sultanpur?

A
45

B
54

C
63

D
72

Solution

Let the distance between Dholakpur and Sultanpur be 'x' miles.
Question 6
3 / -1

In triangle ABC, point D lies on AC such that AD:DC = 1:2. Let E denote the midpoint of BD, and let point F be the intersection of BC and AE (when produced). If the area (in sq. cm) of triangle ABC is 180cm², what is the area of triangle EBF?

A
30

B
45

C
15

D
60

Solution

From (1) and (2), Area of triangle EBF = 15cm².
Question 7
3 / -1

a, b, c are three distinct integers from 2 to 10 (both inclusive). Exactly one of ab, bc and ca is odd. abc is a multiple of 4. The arithmetic mean of a and b is an integer and so is the arithmetic mean of a, b and c. How many such triplets are possible (unordered triplets)?

A
3

B
4

C
6

D
8

Solution

Exactly one of ab, bc and ca is odd => Two are odd and one is even.

abc is a multiple of 4 => the even number is a multiple of 4.

The arithmetic mean of a and b is an integer => a and b are odd.

and so is the arithmetic mean of a, b and c. => a + b + c is a multiple of 3.

c can be 4 or 8 and a,b can be one among 3, 5, 7, 9.

c = 4; a, b can be 3, 5 or 5, 9

c = 8; a, b can be 3, 7 or 7, 9

Four triplets are possible (4, 3, 5), (4, 5, 9), (8, 3, 7), (8, 7, 9),

Therefore, Option (B) is the answer.
Question 8
3 / -1

Out of 40% of the total number of matches, a badminton player has won 8 matches and lost 4 of them. If it's true that no match can end in a tie, what is the maximum number of matches he can lose and still win more than 60% of the total number of matches?

A
6

B
8

C
7

D
9

Solution

19 - 8 = 11 more wins are required out of remaining 18 matches.

Hence, he can lose a maximum of 7 matches.
Question 9
3 / -1

A factory produces three types of products – P, Q, and R. The average cost of producing one unit of product P is Rs.200, for Q is Rs.250, and for R is Rs.300. The number of units produced for P, Q, and R are in the ratio 5:6:9, respectively. During a cost audit, it was found that 40% of the units of product P were defective and had to be reworked, increasing their cost by 25%. Similarly, 30% of the units of product Q were defective, increasing their cost by 30%, and 20% of the units of product R were defective, increasing their cost by 20%. The rest of the units were produced at their original cost. If the selling prices for P, Q, and R are Rs.250, Rs.320, and Rs.380 per unit, respectively, what is the overall percentage profit or loss for the factory?

A
18.89%

B
19.19%

C
17.59%

D
21.29%

Solution

Let the number of units produced for products P, Q, and R be 5x, 6x, and 9x respectively.

The total initial cost of production is calculated as follows:

For product P: 5x × 200 = 1000x

For product Q: 6x × 250 = 1500x

For product R: 9x × 300 = 2700x

Therefore, the total initial cost of production = 1000x + 1500x + 2700x = 5200x

40% of the units of product P were defective, which is 0.4 × 5x = 2x units. The cost of these defective units increased by 25%, so the new cost per defective unit is 200 × 1.25 = 250. The cost

for defective units = 2x × 250 = 500x. The cost for non-defective units (60% or 3x units) = 3x × 200 = 600x.

Total revised cost for product P = 500x + 600x = 1100x

30% of the units of product Q were defective, which is 0.3 × 6x = 1.8x units. The cost of these defective units increased by 30%, so the new cost per defective unit is 250 × 1.30 = 325. The

cost for defective units = 1.8x × 325 = 585x. The cost for non-defective units (70% or 4.2x units) = 4.2x × 250 = 1050x.

Total revised cost for product Q = 585x + 1050x = 1635x

20% of the units of product R were defective, which is 0.2 × 9x = 1.8x units. The cost of these defective units increased by 20%, so the new cost per defective unit is 300 × 1.20 = 360. The

cost for defective units = 1.8x × 360 = 648x. The cost for non-defective units (80% or 7.2x units) = 7.2x × 300 = 2160x.

Total revised cost for product R = 648x + 2160x = 2808x.

Total revised cost for all products = 1100x + 1635x + 2808x = 5543x

The total revenue is as follows:

For product P: 5x × 250 = 1250x

For product Q: 6x × 320 = 1920x

For product R: 9x × 380 = 3420x

Total revenue = 1250x + 1920x + 3420x = 6590x

Overall profit = Total Revenue - Total Cost = 6590x − 5543x = 1047x

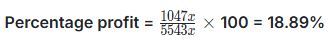
Therefore, the overall percentage profit for the factory is approximately 18.89%.
Question 10
3 / -1

Five men and eight women complete a task in 28 days. If the women are at least half as efficient as the men, but not more efficient than the men, then the possible number of days for 4 women and 3 men to complete the same task lies in the range?

A
30 to 42

B
40 to 48

C
49 to 53

D
55 to 60

Solution