Coordinate Geometry Test

Result

Coordinate Geometry Test - 24

Score
-
out of -
Rank
-
out of -

TIME Taken - -

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Weekly Quiz Competition

Question 1
1 / -0

If point P divides the line joining the points $$(5, 0)$$ and $$(0, 4)$$ in the ratio $$2 : 3$$ internally, then the $$x$$-coordinate of $$P$$ is

A
$$2$$

B
$$1$$

C
$$3$$

D
$$4$$

Solution

The point $$P=\left( X,Y \right)$$ divides the line joining the points $$A=\left( { x }_{ 1 },{ y }_{ 1 } \right) =\left( 5,0 \right)$$
and $$B=\left( { x }_{ 2 },{ y }_{ 2 } \right) =\left( 0,4 \right)$$ in the ratio $$m:n=2:3$$

$$\therefore$$ The abscissa of $$P$$ is $$X=\dfrac { m{ x }_{ 2 }+n{ x }_{ 1 } }{ m+n } =\dfrac { 2\times 0+3\times 5 }{ 2+3 } =3$$
Question 2
1 / -0

If mid point of the line segment joining $$(2a, 4)$$ and $$(-2, 3b)$$ is $$(1, 2a + 1)$$, then the values of $$a$$ and $$b$$ are given by

A
$$a = 2, b = - 2$$

B
$$a = b = 2$$

C
$$a= 1 = b$$

D
$$a= -2, b = 2$$

Solution

Midpoint of any two points $$(p,q)$$ and $$(r,s)$$ is given by
$$M=\left(\dfrac{p+r}{2},\dfrac{q+s}{2}\right)$$
Given points are $$(2a, 4)$$ and $$(-2,3b)$$ and the midpoint is $$(1,2a+1)$$
$$\therefore (1,2a+1)=\left(\dfrac{2a-2}{2},\dfrac{4+3b}{2}\right)$$
$$\implies (1,2a+1)=\left(a-1,\dfrac{4+3b}{2}\right)$$
Now, comparing both sides,
$$ a-1=1$$
$$\implies a=2$$

and,
$$\dfrac{4+3b}{2}=2a+1$$
$$\Rightarrow 4+3b=4a+2$$
$$\Rightarrow 3b=4a+2-4$$
$$\Rightarrow 3b=4\times2-2$$
$$\Rightarrow 3b=6$$
$$\Rightarrow b=2$$

Hence, $$a=b=2$$.
Question 3
1 / -0

The coordinates of $$A$$ and $$B$$ are $$(1, 2) $$ and $$(2, 3)$$. Find the coordinates of $$R $$, so that $$\displaystyle \frac{AR}{RB} = \frac{4}{3}$$.

A
$$\displaystyle \left ( \frac{1}{7} , \frac{3}{7}\right)$$

B
$$\displaystyle \left ( \frac{11}{7} , \frac{18}{7}\right)$$

C
$$\displaystyle \left ( \frac{15}{7} , \frac{3}{7}\right)$$

D
$$\displaystyle \left ( \frac{13}{7} , \frac{4}{5}\right)$$

Solution

Let the coordinates of $$R$$ be $$(x, y)$$, then $$\displaystyle \frac{AR}{RB} = \frac{m_1}{m_2}= \frac{4}{3}$$
Two points are $$A (1, 2) $$ and $$B (2, 3)$$
We know that $$x$$ $$\displaystyle =\frac{m_1x_2 + m_2 x_1}{m_1+m_2} = \frac{4.2 + 3.1}{4+3} = \frac{11}{7}$$
$$\displaystyle y = \frac{m_1y_2 + m_2y_1}{m_1+m_2} = \frac{4.3 + 3.2}{4+3} = \frac{18}{7}$$
Therefore, given point $$R$$ is $$\displaystyle \left ( \frac{11}{7} , \frac{18}{7} \right )$$.
Question 4
1 / -0

The co-ordinates of a point $$R$$ which divides the line joining $$A(-3, 3)$$ and $$B(2, - 7)$$ internally in the ratio $$2 : 3$$ are

A
$$(1, 1)$$

B
$$(-1, - 1)$$

C
$$(2, 2)$$

D
$$(3, 3)$$

Solution

The given points are $$A=\left( { x }_{ 1 },{ y }_{ 1 } \right) =\left( -3,3 \right) , B=\left( { x }_{ 2 },{ y }_{ 2 } \right) =\left( 2,-7 \right)$$
Now, $$R=\left( X,Y \right)$$ divides the line segment AB internally in the ratio $$m:n=2:3$$.
We know $$X=\dfrac { m{ x }_{ 2 }+n{ x }_{ 1 } }{ m+n }$$ and $$Y=\dfrac { m{ y }_{ 2 }+n{ y }_{ 1 } }{ m+n }$$
$$\therefore X=\dfrac { 2\times 2+3\times (-3) }{ 2+3 } =-\dfrac { 5 }{ 5 } =-1$$ and $$Y=\dfrac { 2\times (-7)+3\times 3 }{ 2+3 } =-\dfrac { 5 }{ 5 } =-1$$
$$\therefore \left( X,Y \right) =\left( -1,-1 \right)$$
Question 5
1 / -0

$$M$$ is the midpoint of the straight line $$PQ$$. If $$P$$ is $$(-2, 9)$$ and $$M$$ is (4, 3), find the coordinates of $$Q.$$

A
$$(1, 6)$$

B
$$(10, -3)$$

C
$$(10, 6)$$

D
$$(8, -3)$$

Solution

Let coordinates of $$Q$$ be $$(x, y)$$
and midpoints are given as:
$$\dfrac{x+(-2)}{2}=4
\dfrac{y+9}{2}=3$$
$$x-2=8\\ y+9=6$$
$$\Rightarrow x=10\\ \Rightarrow y=-3$$
$$\therefore (10, -3)$$ are coordinates of $$Q$$.
Question 6
1 / -0

The Point $$A$$ on x-axis and point $$B$$ on y-axis and the mid-point of the line segment AB is shown in the figure is $$(4 - 3)$$. Then, the co-ordinates of A and B are

A
$$(8, 0)$$ and $$(0, - 6)$$

B
$$(0, 8)$$ and $$(0, - 6)$$

C
$$(8, 0)$$ and $$(-6, 0)$$

D
None of these

Solution

$$A= (x, 0), B= (0, y)$$
$$4= \dfrac{x+0}{2}$$
$$x= 8$$
$$-3= \dfrac{0+y}{2}$$
$$y= -6$$
Hence $$A= (8,0)\ and\ B=(0,-6)$$
Question 7
1 / -0

If the line joining points $$(5, -6)$$ and $$(9, 8)$$ divided by a point R internally in $$5 : 6$$ ratio, then R =

A
($$\dfrac {5}{11}, \dfrac {4}{11}$$)

B
($$\dfrac {75}{11}, \dfrac {76}{11}$$)

C
($$\dfrac {75}{11}, \dfrac {4}{11}$$)

D
None of these

Solution

The given points are $$A=\left( { x }_{ 1 },{ y }_{ 1 } \right) =\left( 5, -6 \right) , B=\left( { x }_{ 2 },{ y }_{ 2 } \right) =\left( 9,8 \right)$$
Now, $$R=\left( X,Y \right)$$ divides the line segment AB internally in the ratio $$m:n=5:6$$.
We know $$X=\dfrac { m{ x }_{ 2 }+n{ x }_{ 1 } }{ m+n }$$ and $$Y=\dfrac { m{ y }_{ 2 }+n{ y }_{ 1 } }{ m+n }$$
$$\therefore X=\dfrac { 5\times 9+6\times 5 }{ 5+6 } =\dfrac {7 5 }{ 11 }$$ and $$Y=\dfrac { 5\times 8+6\times (-6 )}{ 5+6} =\dfrac { 4 }{ 11} $$
Therefore, given point $$R$$ is $$\displaystyle \left ( \frac{75}{11} , \frac{4}{11} \right )$$.
Question 8
1 / -0

If (2, 1), (4, 5), (-1, - 3) are the mid points of the sides of a triangle, then the co-ordinates of its vertices are

A
$$(- 3, -7), (17, 9), (1, 1)$$

B
$$(-3. 7), (7, 9), (- 1, 1)$$

C
$$(-3, - 7), (7, 9), (1, 1)$$

D
none

Solution

Let $$A(x_1,y_1),\,B(x_2,y_2),\, C(x_3,y_3)$$ be the vertices of $$\triangle ABC$$
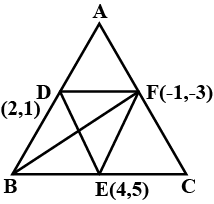
Let D(2,1) , F(-1,-3) and E(4,5) be the mid points of AB,AC and BC.
D and F are mid points pf ABC and AC
$$\therefore DF\parallel BE$$
E and F are mid points pf BC and Ac
$$\therefore EF\parallel BD$$
$$\therefore$$ DBEF is a parallelogram.
The diagonals of a parallelogram bisect each other i.e, both diagonals have same mid point
i.e, Midpoint BF=Midpoint of DE
$$\left( \dfrac { { x }_{ 2 }+(-1) }{ 2 } ,\dfrac { { y }_{ 2 }+(-3) }{ 2 } \right) =\left( \dfrac { 2+4 }{ 2 } ,\dfrac { 1+5 }{ 2 } \right) \\ \therefore \dfrac { { x }_{ 2 }+(-1) }{ 2 } =\dfrac { 2+4 }{ 2 } \quad \therefore { x }_{ 2 }=7$$
Similarly $$\dfrac { { y }_{ 2 }+(-3) }{ 2 } =\dfrac { 1+5 }{ 2 } \quad \therefore { y }_{ 2 }=9\\ i.e,\left( { x }_{ 2 },{ y }_{ 2 } \right) =\left( 7,9 \right) $$
D is the mid point of AB
$$D=(2,1)=\left( \dfrac { { x }_{ 1 }+{ x }_{ 2 } }{ 2 } ,\dfrac { { y }_{ 1 }+{ y }_{ 2 } }{ 2 } \right) \\ \dfrac { { x }_{ 1 }+7 }{ 2 } =2\quad \quad \quad \therefore { \quad x }_{ 1 }=-3\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad i.e,({ x }_{ 1 },{ y }_{ 1 })=\left( -3,-7 \right) \\ \dfrac { { y }_{ 1 }+9 }{ 2 } =1\quad \therefore { y }_{ 1 }=-7$$
F is the midpoint of AC
$$F=\left( -1,-3 \right) =\left( \dfrac { { x }_{ 1 }+{ x }_{ 3 } }{ 2 } ,\dfrac { { y }_{ 1 }+{ y }_{ 3 } }{ 2 } \right) \\ -1=\dfrac { -3+{ x }_{ 3 } }{ 2 } \quad \therefore \quad { x }_{ 3 }=1\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad i.e,({ x }_{ 3 },{ y }_{ 3 })=(1,1)\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ -3=\dfrac { -7+{ y }_{ 3 } }{ 2 } \quad \therefore \quad { y }_{ 3 }=1$$
$$\therefore$$ The vertices of triangle are $$=(-3,-7),(7,9),(1,1)$$
Question 9
1 / -0

The diagram is on a Cartesian plane.
If the midpoints of PQ and RS are the same, the coordinates of S are:

A
(0, 2)

B
(3, 4)

C
(0, 6)

D
(2, 0)

Solution

$$P(-2, 6); Q(4, 2);R(2, 6)$$
Mid-point pf PQ $$=\left ( \dfrac{-2+4}{2}, \dfrac{6+2}{2} \right )$$
Let coordinates of S be (x, y) then, $$ \dfrac{x+2}{2}=1; \dfrac{y+2}{2}=4$$
$$x=0; y=2$$
$$(0, 2)$$ are the coordinates of $$S$$
Question 10
1 / -0

If the coordinates of the mid points of the sides of the triangle are (1, 2), $$(0,   -1)$$ and $$ (2,   -1)$$. Find the coordinates of its vertices.

A
$$(1,   -4), (3,   2), (-1,   2)$$

B
$$(1, 4), (3,   2), (-1,   2)$$

C
$$(1,   -4), (3,   2), (1,   2)$$

D
$$(1,   -4), (3, -2), (-1,   2)$$

Solution

User

Question Analysis

Correct -
Wrong -
Skipped -

My Perfomance

Score
-
out of -
Rank
-
out of -

Re-Attempt Weekly Quiz Competition

Coordinate Geometry Test - 24

Result

Coordinate Geometry Test - 24

Score

-

Rank

-

SHARING IS CARING

Question 1

$$2$$

$$1$$

$$3$$

$$4$$

Solution

Question 2

$$a = 2, b = - 2$$

$$a = b = 2$$

$$a= 1 = b$$

$$a= -2, b = 2$$

Solution

Question 3

$$\displaystyle \left ( \frac{1}{7} , \frac{3}{7}\right)$$

$$\displaystyle \left ( \frac{11}{7} , \frac{18}{7}\right)$$

$$\displaystyle \left ( \frac{15}{7} , \frac{3}{7}\right)$$

$$\displaystyle \left ( \frac{13}{7} , \frac{4}{5}\right)$$

Solution

Question 4

$$(1, 1)$$

$$(-1, - 1)$$

$$(2, 2)$$

$$(3, 3)$$

Solution

Question 5

$$(1, 6)$$

$$(10, -3)$$

$$(10, 6)$$

$$(8, -3)$$

Solution

Question 6

$$(8, 0)$$ and $$(0, - 6)$$

$$(0, 8)$$ and $$(0, - 6)$$

$$(8, 0)$$ and $$(-6, 0)$$

None of these

Solution

Question 7

($$\dfrac {5}{11}, \dfrac {4}{11}$$)

($$\dfrac {75}{11}, \dfrac {76}{11}$$)

($$\dfrac {75}{11}, \dfrac {4}{11}$$)

None of these

Solution

Question 8

$$(- 3, -7), (17, 9), (1, 1)$$

$$(-3. 7), (7, 9), (- 1, 1)$$

$$(-3, - 7), (7, 9), (1, 1)$$

none

Solution

Question 9

(0, 2)

(3, 4)

(0, 6)

(2, 0)

Solution

Question 10

$$(1, -4), (3, 2), (-1, 2)$$

$$(1, 4), (3, 2), (-1, 2)$$

$$(1, -4), (3, 2), (1, 2)$$

$$(1, -4), (3, -2), (-1, 2)$$

Solution

User

Question Analysis

My Perfomance

Score

-

Rank

-

Results Announcement on: coming Monday

Stay Tuned: We’ll update you on your result via email or SMS.