Coordinate Geometry Test

Result

Coordinate Geometry Test - 46

Score
-
out of -
Rank
-
out of -

TIME Taken - -

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Weekly Quiz Competition

Question 1
1 / -0

$$ \mathrm{ABC} $$ is a triangle and $$ \mathrm{D} $$ is a mid point of $$ \mathrm{BC} $$. If the co-ordinate of vertices of $$ \triangle \mathrm{ABC} $$ are (1,2),(-1,-3) and (3,-5) respectively then co-ordinate of the point divides $$ A D $$ internally in the ratio 2: 1 will be :

A
(1,-6)

B
(-1,6)

C
(-1,-6)

D
(1,-2)

Solution

Co-ordinate of mid point D of BC $$ =\left(\dfrac{-1+3}{2}, \dfrac{-3-5}{2}\right) $$
$$ =(1,-4) $$
The co-ordinate of a point divide $$ A(1,2) $$ and $$ D(1,-4) $$ internally in the ratio 2: 1 $$ =\left(\dfrac{2(1)+(1)(1)}{2+1}, \dfrac{2(-4)+1(2)}{2+1}\right)=(1,-2) $$
$$ \therefore $$ Co-ordinate of a point $$ =(1,-2) $$
Question 2
1 / -0

The coordinated of the midpoint of the line segment joining points (6,8) and (2,4) will be:

A
(4,6)

B
(6,4)

C
(2,2)

D
(1,0)

Solution

Let the coordinates of the midpoint of $$(6,8)$$ and $$(2,4)$$ be $$ (x, y) $$.

We know that the coordinates of the midpoint of the line segment joining $$(x_1,y_1) \ and\ (x_2,y_2)$$ are:

$$P(x,y)=\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)$$

$$\therefore \ x=\dfrac{6+2}{2}=\dfrac{8}{2}=4 $$

And $$ y=\dfrac{8+4}{2}=\dfrac{12}{2}=6 $$

Hence, coordinates of the midpoint are $$ (4,6) $$.
Question 3
1 / -0

The line $$\displaystyle 3x+2y=24$$ meets x-axis at A and y-axis at B. The perpendicular bisector of $$\displaystyle \overline { AB } $$ meets the line through (0, -1) and parallel to x-axis at C. Find the area of $$\displaystyle \Delta ABC$$.

A
85 $$\displaystyle { units }^{ 2 }$$

B
87 $$\displaystyle { units }^{ 2 }$$

C
90 $$\displaystyle { units }^{ 2 }$$

D
91 $$\displaystyle { units }^{ 2 }$$

Solution
Question 4
1 / -0

If the coordinates of the mid points of the sides of a triangle are $$(1,2),(0,-1)$$ and $$(2,-1)$$. Find the coordinates of its vertices.

A
$$(1,4), (-3,2), (1-2)$$

B
$$(1,-4), (3,2), (-1,2)$$

C
$$(1,-4), (-3,2), (1,-2)$$

D
$$(-1,4), (3,2), (-1,2)$$

Solution

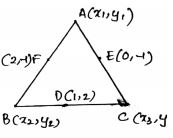
Let $$A({ x }_{ 1 }{ y }_{ 1 }),\quad B({ x }_{ 2 },{ y }_{ 2 })\quad and\quad C({ x }_{ 3 },{ y }_{ 3 })\quad $$ be the vertices of $$\triangle$$ABC.
Let D(1,2) ,E(0,-1) and F(2,-1) be the mid -points of sides BC,AC and AB
Since D is the mid point of BC.
$$A({ x }_{ 1 }{ y }_{ 1 }),\quad B({ x }_{ 2 },{ y }_{ 2 })\quad and\quad C({ x }_{ 3 },{ y }_{ 3 })\quad \\ \therefore \dfrac { { x }_{ 2 }+{ x }_{ 3 } }{ 2 } =1\quad and\quad \dfrac { { y }_{ 2 }+{ y }_{ 3 } }{ 2 } =2\\ \Longrightarrow { x }_{ 2 }+{ x }_{ 3 }=2\quad { y }_{ 2 }+{ y }_{ 3 }=4 \rightarrow$$ (i)
Similarly , E and F are the mid-points of CA and Ab respectively
$$\therefore \dfrac { { x }_{ 1 }+{ x }_{ 3 } }{ 2 } =0\quad and\quad \dfrac { { y }_{ 1 }+{ y }_{ 3 } }{ 2 } =-1\\ \Longrightarrow { x }_{ 1 }+{ x }_{ 3 }=2\quad and\quad { y }_{ 1 }+{ y }_{ 3 }-2 \rightarrow(2)\\ \therefore \dfrac { { x }_{ 1 }+{ x }_{ 2 } }{ 2 } =2\quad and\quad \dfrac { { y }_{ 1 }+{ y }_{ 2 } }{ 2 } =-1\\ \Longrightarrow { x }_{ 1 }+{ x }_{ 2 }=4\quad and\quad { y }_{ 1 }+{ y }_{ 2 }=-2 \rightarrow(3)$$
From (1),(2),and(3)
$$({ x }_{ 2 }+{ x }_{ 3 })+({ x }_{ 1 }+{ x }_{ 3 })+({ x }_{ 1 }+{ x }_{ 2 })=2+0+4\\ ({ y }_{ 2 }+{ y }_{ 3 })+({ y }_{ 1 }+{ y }_{ 3 })+({ y }_{ 1 }+{ y }_{ 2 })=4-2-2\\ \Longrightarrow { x }_{ 1 }+{ x }_{ 2 }+{ x }_{ 3 }=3\quad and\quad { y }_{ 1 }+{ y }_{ 2 }+{ y }_{ 3 }=0 \rightarrow (4)$$
From (1) and (4)
$${ x }_{ 1 }+{ 2 }=3\quad and\quad { y }_{ 1 }+4=0\\ \Longrightarrow { x }_{ 1 }=1\quad and\quad { y }_{ 1 }=-4 \quad \therefore (1,-4)$$
From (2) and (4)
$${ x }_{ 2 }+0=3\quad and\quad { y }_{ 2 }-2=0\\ \Longrightarrow ({ x }_{ 2 },{ y }_{ 2 })=B(3,2)$$
From (3) and (4)
$${ x }_{ 3 }+4=3\quad and\quad { y }_{ 3 }-2=0\\ \therefore ({ x }_{ 3 },{ y }_{ 3 })=C(-1,2)$$
$$\therefore$$ Coordinate of $$\triangle$$ABC are $$\Rightarrow$$ $$(1,-4); B(3,2); C(-1,2)$$
Question 5
1 / -0

If four points are $$A(6,3),B(-3,5),C(4,-2)$$ and $$P(x,y),$$ then the ratio of the areas of $$\triangle PBC$$ and $$\triangle ABC$$ is:

A
$$\displaystyle \frac { x+y-2 }{ 7 } $$

B
$$\displaystyle \frac { x-y-2 }{ 7 } $$

C
$$\displaystyle \frac { x-y+2 }{ 2 } $$

D
$$\displaystyle \frac { x+y+2 }{ 2 } $$

Solution

Given: Coordinates of points $$\displaystyle A\left( { x }_{ 1 },{ y }_{ 1 } \right) =\left( 6,3 \right) ,B\left( { x }_{ 2 },{ y }_{ 2 } \right) =\left( -3,5 \right) ,C\left( { x }_{ 3, }{ y }_{ 3 } \right) =\left( 4,-2 \right) $$ and $$\displaystyle P\left( x,y \right) .$$

We know that the area of:
$$\displaystyle\triangle PBC=\frac { 1 }{ 2 } \left[ x\left( { y }_{ 2 }-{ y }_{ 3 } \right) +{ x }_{ 3 }\left( y-{ y }_{ 2 } \right) +{ x }_{ 2 }\left( { y }_{ 3 }-y \right) \right] $$

$$\displaystyle=\frac { 1 }{ 2 } \left[ x\left( 5+2 \right) +4\left( y-5 \right) -3\left( -2-y \right) \right] $$ $$\displaystyle=\frac { 1 }{ 2 } \left[ 7x+7y-14 \right] $$

Similarly, the area of

$$\displaystyle\triangle ABC=\frac { 1 }{ 2 } \left[ { x }_{ 1 }\left( { y }_{ 2 }-{ y }_{ 3 } \right) +{ x }_{ 2 }\left( { y }_{ 3 }-{ y }_{ 1 } \right) \right] +{ x }_{ 3 }\left( { y }_{ 1 }-{ y }_{ 2 } \right) $$

$$\displaystyle=\dfrac{1}{2}[6\left( 5+2 \right) -3\left( -2-3 \right) +4\left( 3-5 \right)] =\dfrac{49}{2}$$

Therefore, the ratio of the areas of $$\triangle PAB$$ and $$\triangle ABC$$

$$\displaystyle=\frac { 7x+7y-14 }{ 49 } =\frac { 7\left( x+y-2 \right) }{ 49 } =\frac { x+y-2 }{ 7 } $$
Question 6
1 / -0

$$\text{Q}, \text{R}$$ and $$\text{S}$$ are the points on the line joining the points $$\text{P}(a, x)$$ and $$\text{T}(b, y)$$ such that $$\text{PQ=QR=RS=ST}$$, then $$\displaystyle \left ( \frac{5a+3b}{8}, \frac{5x+3y}{8} \right )$$ is the mid point of the segment :

A
$$\text{PQ}$$

B
$$\text{QR}$$

C
$$\text{RS}$$

D
$$\text{ST}$$

Solution

$$PQ=QR=RS=ST$$ ---(Given)
Also points $$P,Q,R,S$$ and $$T$$ are on the same line segment.
$$\Rightarrow R $$ is the midpoint of $$PT$$
$$\therefore$$ co-ordinates of $$R$$ can be obtained by midpoint formula.
$$R \equiv \bigg(\dfrac{a+b}{2},\dfrac{x+y}{2}\bigg)$$

$$PQ=QR$$ .....(given)
$$\therefore Q $$ is the midpoint of $$PR$$
$$Q \equiv \Bigg[\dfrac {a+\bigg(\dfrac {a+b}{2}\bigg)}{2}, \dfrac {x+\bigg(\dfrac{x+y}{2}\bigg)}{2}\Bigg]$$
$$Q \equiv \bigg(\dfrac{3a+b}{4},\dfrac{3x+y}{4}\bigg)$$

Suppose $$A$$ is midpoint of $$QR$$ :
$$A \equiv \Bigg[\dfrac{ \bigg(\dfrac{3a+b}{4} \bigg)+\bigg(\dfrac {a+b}{2}\bigg)}{2},\dfrac{\bigg(\dfrac{3x+y}{4}\bigg)+\bigg(\dfrac{x+y}{2}\bigg)} {2}\Bigg]$$
$$A \equiv \Bigg[\dfrac{ \bigg(\dfrac{3a+b+2a+2b}{4} \bigg)}{2},\dfrac{\bigg(\dfrac{3x+y+2x+2y}{4}\bigg)} {2}\Bigg]$$
$$A \equiv \bigg(\dfrac{5a+3b}{8},\dfrac{5x+3y}{8}\bigg)$$

Hence, option $$\text{B}$$ is correct.
Question 7
1 / -0

The lengths of the medians of $$\bigtriangleup$$ ABC whose vertices are $$A(7,-3), B(5,3)$$ and $$C(3,-1)$$ are

A
Medians: $$AD=5$$ units, $$BE={ 5 }$$ units & $$CF=\sqrt { 5 }$$ units

B
Medians: $$AD=5$$ units, $$BE=\sqrt { 10 }$$ units & $$CF=\sqrt { 10 }$$ units

C
Medians $$AD=5$$ units, $$BE={ 5 }$$ units & $$CF=\sqrt { 10 }$$ units

D
Medians $$AD=10$$ units, $$BE=\sqrt { 5 }$$ units & $$CF=\sqrt { 10 }$$ units

Solution

Co-ordinate of D :
$$\because D$$ is a midpoint of $$BC$$
$$\therefore D_x= \dfrac{C_x+B_x}{2}=\dfrac{3+5}{2}=4$$
$$\therefore D_y= \dfrac{C_y+B_y}{2}=\dfrac{-1+3}{2}=1$$
$$\Rightarrow D\equiv(4,1)$$

Co-ordinate of E :
$$\because E$$ is a midpoint of $$AC$$
$$\therefore E_x= \dfrac{A_x+C_x}{2}=\dfrac{7+3}{2}=5$$
$$\therefore E_y= \dfrac{A_y+C_y}{2}=\dfrac{-3-1}{2}=-2$$
$$\Rightarrow E\equiv(5,-2)$$

Co-ordinate of F :
$$\because F$$ is a midpoint of $$AB$$
$$\therefore F_x= \dfrac{A_x+B_x}{2}=\dfrac{7+5}{2}=6$$
$$\therefore F_y= \dfrac{A_y+B_y}{2}=\dfrac{-3+3}{2}=0$$
$$\Rightarrow F\equiv(6,0)$$

Length Of medians can be obtained Using Distance Formula
$$d=\sqrt{(x_2-x_1)^2+(y_2-y1)^2}$$

$$\therefore AD=\sqrt{(4-7)^2+(1-(-3))^2}$$
$$\therefore AD=\sqrt{9+16}$$
$$\therefore AD=5$$

$$\therefore BE=\sqrt{(5-5)^2+(-2-3)^2}$$
$$\therefore BE=\sqrt{0+25}$$
$$\therefore BE=5$$

$$\therefore CF=\sqrt{(6-3)^2+(0-(-1))^2}$$
$$\therefore CF=\sqrt{9+1}$$
$$\therefore CF=\sqrt{10}$$

Hence, option $$C$$ is correct.
Question 8
1 / -0

The mid point of the segment joining $$(2a, 4)$$ and $$(-2, 2b)$$ is $$(1, 2a+1)$$, then value of b is

A
$$2$$

B
$$1$$

C
$$3$$

D
$$-1$$

Solution

Mid point of two points $$ { (x }_{ 1 },{ y }_{ 1 }) $$ and $$ { (x }_{ 2

},{ y }_{ 2 }) $$ is calculated by the formula $$ \left( \frac { { x }_{

1 }+{ x }_{ 2 } }{ 2 } ,\frac { { y }_{ 1 }+y_{ 2 } }{ 2 } \right) $$

Given, midpoint of $$ (2a,4) $$ and $$ (-2,2b) = (1,2a+1) $$

$$ => \left( \frac {2a -2 }{ 2 } ,\frac { 4 + 2b }{ 2 } \right) \quad

= (1, 2a + 1) $$

$$ => \frac {2a-2 }{ 2 } = 1 ; \frac { 4 + 2b }{ 2 } = 2a + 1 $$

$$ => 2a-2 = 2 ; 4 + 2b = 4a + 2 $$

$$=> a = 2 $$
So, $$ 4 + 2b = 8 + 2 $$
$$=> 4 + 2b = 10 $$
$$ => 2b = 6 $$
$$ b = 3 $$
Question 9
1 / -0

Directions For Questions

The area of a triangle whose vertices are $$\displaystyle \left( { x }_{ 1 },{ y }_{ 1 } \right) ,\left( { x }_{ 2 },{ y }_{ 2 } \right) $$ and $$\displaystyle \left( { x }_{ 3 },{ y }_{ 3 } \right) $$ is given by $$\displaystyle \Delta =\frac { 1 }{ 2 } \left| { x }_{ 1 }\left( { y }_{ 2 },{ y }_{ 3 } \right) +{ x }_{ 2 }\left( { y }_{ 3 },{ y }_{ 1 } \right) +{ x }_{ 3 }\left( { y }_{ 1 },{ y }_{ 2 } \right) \right| $$. The points $$\displaystyle \left( { x }_{ 1 },{ y }_{ 1 } \right) ,\left( { x }_{ 2 },{ y }_{ 2 } \right) $$ and $$\displaystyle \left( { x }_{ 3 },{ y }_{ 3 } \right) $$ are collinear of $$\displaystyle \Delta =0$$

...view full instructions

Determine the area of the triangle whose vertices are $$\displaystyle \left( \frac { 1 }{ 2 } ,\frac { -1 }{ 2 } \right) ,\left( 2,\frac { -1 }{ 2 } \right) $$ and $$\displaystyle \left( 2,\frac { \sqrt { 3 } -1 }{ 2 } \right) $$.

A
$$\displaystyle 3\sqrt { 3 } $$

B
$$\displaystyle \frac { 3\sqrt { 3 } }{ 8 } $$

C
$$\displaystyle 12\sqrt { 3 } $$

D
$$\displaystyle \frac { 3\sqrt { 3 } }{ 4 } $$

Solution
Question 10
1 / -0

If (2, 1), (-1, -2), (3, 3) are midpoints of sides BC, CA, AB of $$\displaystyle \Delta ABC$$, find the equation of AB. (A) x-y=1/2 (13) x+y= 1 (C) x-y=9 (D) x=y

A
$$\displaystyle x-y=1/2$$

B
$$\displaystyle x+y=1$$

C
$$\displaystyle x-y=9$$

D
$$\displaystyle x=y$$

Solution