Linear Programming Test - 31

Given

Objective function

Maximize, \(Z=x_{1}+2 x_{2}\)

Constraints

\(x_{1} \leq 2 \)

\(x_{2} \leq 2 \)

\(x_{1}+x_{2} \leq 2 \)

Non neagative constarints

\(\mathrm{x}_{1}, \mathrm{x}_{2} \geq 0\)

The above equations can be written as,

\(\frac{x_{1}}{2} \leq 1 \)

\(\frac{x_{2}}{2} \leq 1 \)

\(\frac{x_{1}}{2}+\frac{x_{2}}{2} \leq 1\)

Plot the above equations on \(x_{1}-x_{2}\) graph and find out the solution space.

Now, find out the value of the objective function at every extreme point of solution space.

\(Z=x_{1}+2 x_{2}\)

\(Z_{0}=0+2 \times 0=0 \)

\(Z_{A}=0+2 \times 2=4 \)

\(Z_{B}=2+2 \times 0=2\)

Since the value of the objective function is maximum at \(A\). There \(A(0,2)\) is the optimal solution.

Given:

\(Z=7 x+y\) subject to \(5 x+y \geq 5, x+y \geq 3, x \geq 0, y \geq 0\)

First we draw the lines \(A B\) and \(C D\) whose equations are \(5 x+y=5\) and \(x+y=3\) respectively.

\(\begin{array}{|l|l|l|l|l|l|} \hline \text{Line} & \text{Inequation} & \text{Points on x} & \text{Points on y} & \text{Sign} & \text{Feasible region} \\ \hline AB & 5 x+y=5 & A(1,0) & B(0,5) & \geq & \text{Non - origin side A B} \\ \hline CD & x+y=3 & C(3,0) & D(0,3) & \geq & \text{Non - origin side of line CD} \\ \hline \end{array}\)

1 unit \(=1 \mathrm{~cm}\) both axis

common feasible region BPC

\(\begin{array}{|l|l|} \hline \text{Points} & \text{Minimize} z=7 x+y \\ \hline B(0,5) & Z(B)=7(0)+5=5 \\ \hline P\left(\frac{1}{2}, \frac{5}{2}\right) & Z(P)=7 \times \frac{1}{2}+\frac{5}{2}=6 \\ \hline C(3,0) \quad & Z(C)=7 ×(3)+0=21 \\ \hline \end{array}\)

\(Z\) is minimum at \(x=0, y=5\) and \(\min (Z)=5\)

Given:

\(\mathrm{z}=2 \mathrm{x}+5 \mathrm{y}\)

\(2 \mathrm{x}+4 \mathrm{y} \leq 8 \)

\(\Rightarrow \mathrm{x}+2 \mathrm{y} \leq 4\)

\(3 x+y \leq 6, x+y \leq 4, x \geq 0, y \geq 0\)

Draw the lines \(\mathrm{x}+2 \mathrm{y}=4\) (passes through (4,0\(),(0,2))\)

\(3 \mathrm{x}+\mathrm{y}=6\) (passes through \((2,0),(0,6)\) and

\(\mathrm{x}+\mathrm{y}=4\) (passes through \((4,0),(0,4)\)

Shade the region satisfied by the given inequations;

The shaded region in the figure gives the feasible region determined by the given inequations.

Solving \(3 \mathrm{x}+\mathrm{y}=6\) and \(\mathrm{x}+2 \mathrm{y}=4\) simultaneously, we get

\(\mathrm{x}=\frac{8}{5}\) and \(\mathrm{y}=\frac{6}{5}\)

We observe that the feasible region \(\mathrm{OABC}\) is a convex polygon and bounded and has corner points.

\(\mathrm{O}(0,0), \mathrm{A}(2,0), \mathrm{B}\left(\frac{8}{5}, \frac{6}{5}\right), \mathrm{C}(0,2)\)

The optimal solution occurs at one of the corner points.

At \(\mathrm{O}(0,0), \mathrm{z}=2×0+5×0=0\)

At \(\mathrm{A}(2,0),~~ \mathrm{z}=2×2+5×0=4\)

At B \(\left(\frac{8}{5}, ~~\frac{6}{5}\right), z=2 × \frac{8}{5}+5 × \frac{6}{5}=\frac{46}{5}\)

At \(\mathrm{C}(0,2),~~ \mathrm{z}=2×0+5×2=10\)

Therefore, z maximum value at \(\mathrm{C}\) and maximum value \(=10\)

The mathematical formulation of the LPP is:

Maximize: \(P=7 X+5 Y \) \(\dots\) (i)

Subject to:

\( 240 \geq 4 X+3 Y\) \(\dots\) (ii)

\(100 \geq 2 X+Y\) \(\dots\) (iii)

\( X \geq 0, Y \geq 0\) \(\dots\) (iv)

From equation (ii) and (iii)

\(140 \geq 2 X+2Y\)

\(70 \geq X+Y\) \(\dots\) (v)

Multiply equation (v) with 3 then substract it from equation (ii), we get,

\(30 \geq X\)

Put value of \(X\) in equation (ii)

\(240 \geq 120+3Y\)

\(40 \geq Y\)

To find the optimal solution to this LP using the graphical method we first identify the region of feasiblesolutions and the corner points of the of the feasible region. The graph for this is plotted below:

In this, the corner points are \((0,0),(50,0)\), \((30,40)\) and \((0,80)\). Testing these corner points on \(P=7 X+5 Y\) gives:

It is given that \(z= ~3 x+2 y\) and it is subject to constraints:

\(~x+2y \leq 10 \)

\(~3 x+y \leq 15 \)

\(x ,\) \(y \geq 0\)

Converting inequalities into equation format:

\(x+2y = 10 \)...(1)

\(~3 x+y = 15 \) ...(2)

The corner points of this common region (shaded region) are: \(O(0,0), C (5,0), E(4,3)\) and \(B(0,5).\)

\(x+2y= 10\) and \(3x+ y = 15\) intersects at E. From (1) and (2) coordinates of \(E\) is \((4,3)\).

Linear Programming: Linear programming is an important optimization (maximization or minimization) technique used in decision making in business and every - day life for obtaining the maximum or minimum values as required of linear expression, subjected to satisfy a certain number of given linear restrictions.

Linear programming problem (LPP): The linear programming problem is general calls for optimizing (maximizing/minimizing) a linear function of variables called the objective function subject to a set of linear equations and/or linear inequations called the constraints or restrictions.

The function which is to be optimized (maximized or minimized) is called the objective function.

The system of linear inequations (or equations) under which the objective function is to be optimized are called the constraints.

A primary requirement of an LPP is that both the objective function and all the constraints must be expressed in terms of linear equations and inequalities.

\(\mathrm{x}=(7+4 \sqrt{3})^{2 \mathrm{n}} \)

\(\mathrm{x}=3+\mathrm{f}\)

\(\mathrm{f}\) is fractional part of \(\mathrm{x}\):

\( 0<\mathrm{f}<1\)

Let \(\mathrm{f}^{\prime}=(7-4 \sqrt{3})^{2 \mathrm{n}}\)

\(0<7-4 \sqrt{3}<1 \)

\(0<(7-4 \sqrt{3})^{\mathrm{n}}<1 \)

\(0<\mathrm{f}^{\prime}<1\)

\(\mathrm{I}+\mathrm{f}+\mathrm{f}^{\prime}=2\left[{ }^{2 \mathrm{n}} \mathrm{C}_{0}(7)^{2 \mathrm{n}}+{ }^{2 \mathrm{n}} \mathrm{C}_{2}(7)^{2 \mathrm{n}-2}+\ldots\right] \)

\(=\text { even }\)

\(0+\mathrm{f}+\mathrm{f}^{\prime}<2\) is integer

\({ }^{\prime} \mathrm{I}^{\prime}\) is integer and \(\mathrm{f}+\mathrm{f}^{\prime}\) is also integer.

\(\Rightarrow \mathrm{f}+\mathrm{f}^{\prime}=1\)

\(\mathrm{f}^{\prime}=1-\mathrm{f} \)

\(\mathrm{x}(1-\mathrm{f})=\mathrm{xf}^{\prime}=(7+4 \sqrt{3})^{2 \mathrm{n}}(7-4 \sqrt{3})^{2 \mathrm{n}} \)

\(=1\)

Given:

Min \(Z=3 x+5 y \)

\(2 x+3 y \geq 12 .......(i)\)

\(-x+y \leq 3 .......(ii)\)

\(x \leq 4, y \geq 3, x \geq 0, y \geq 0\)

Taking equation (i)

\(2 x+3 y=12\)

Putting \(x=0, y=4\) Let the point is \((0,4)\).

Now putting \(y=0, x=6\) Let the point is \((6,0)\).

Now taking equation (ii)

\(-x+y=3\)

Putting \(x=0, y=3(0,3)\)

Putting \(y=0, x=-3(-3,0)\)

The graph is as follows:

ABCDA be the feasible region bounded by these lines Now we find the coordinates of A, B, C and D for A, Solving the equations \(2 x+3 y=12\) and \(-x y=3\). We get:

\(x=\frac{+3}{5} \text { and } y=\frac{18}{5}\)

For coordinate of \(A\left(\frac{+3}{5}, \frac{18}{5}\right)\)

Now

\(Z=3 \times\left(+\frac{3}{5}\right)+5 \times \frac{18}{5} \)

\(=\frac{+9}{5}+\frac{90}{5}=\frac{90}{5}\)

For coordinate of B:

Solving the equations:

\(2 x+3 y=12\) and \(y=3\)

We get \(x=\frac{3}{2}, y=3\)

\(\therefore\) Coordinate of \(B\left(\frac{3}{2}, 3\right)\)

Now \(Z=3 \times \frac{3}{2}+5 \times 3\)

\(=\frac{9}{2}+15=\frac{39}{2}\)

For coordinate of \(C\):

Solving the equations:

\(x=4\) and \(y=3\)

\(\therefore\) Coordinate of \(C(4,3)\)

Now \(Z=3 \times 4+5 \times 3\)

\(=12+1=27\)

For coordinate of \(D\):

Solving the equations:

\(-x+y=3\) and \(x=4\)

We get \(x=4, y=7\)

Now \(Z=3 \times 4+5 \times 7\)

\(=12+35=47\)

\(\operatorname{Min} \mathrm{Z}=\frac{39}{2}\), for \(x=\frac{3}{2}, y=3\)

\(Z=3 x+5 y\)

\(x+3 y \geq 3, x+y \geq 2\) and \(x \geq 0, y \geq 0\)

Converting the given in equations into equations

\(x+3 y=3\)

\(x+y=2\)

Reglon represented by \(x+3 y \geq 3\) :

The line \(x+3 y=3\) meets the coordinate axis at \(\mathrm{A}(3,0)\) and \(\mathrm{B}(0,1)\)

\(x+3 y=3\)

\(\begin{array}{|l|l|l|} \hline \mathrm{x} & 3 & 0 \\ \hline \mathrm{y} & 0 & 1 \\ \hline \end{array}\)

\(\mathrm{A}(3,0) ; \mathrm{B}(0,1)\)

Join the points \(\mathrm{A}\) to 5 to obtain a line.

Clearly \((0,0)\) does not satisfy the in equation \(x+3 y \geq 3\).

So the region opposite to the origin, represents the solution set of the in equation.

Reglon represented by \(x+y \geq 2\) :

The line \(x+y=2\) meets the coordinate axis at points \(C(2,0)\) and \(D(0,2)\). \(x+y=2\)

\(\begin{array}{|l|l|l|} \hline x & 2 & 0 \\ \hline y & 0 & 2 \\ \hline \end{array}\)

\(C(2,0) ; \mathrm{D}(0,2)\)

Join the points \(C\) to \(D\) to obtain the line.

Clearly \((0,0)\) does not satisfy the in equation \(x+y \geq 2\)

So the region opposite to origin, represents the solution set of the in equation.

Reglon represented by \(x \geq 0, y \geq 0\) :

Since every point in the first quadrant satisfies these in equations.

So the first quadrant is the region represented by the equations \(x \geq 0, y \geq 0\).

The point of intersection of lines \(x+3 y=3\) and \(x+y=2\) is \(E(\frac{3 }{ 2}, \frac{1 }{ 2})\)

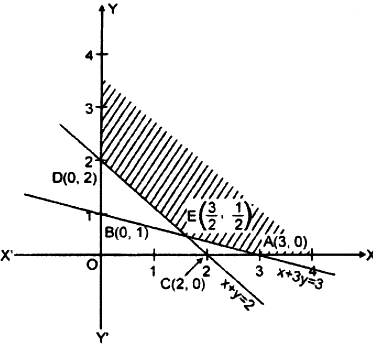
The shaded region A ED is an open and common region of given in equations. This is the proper solution of the given linear programming problem.

The coordinates of the shaded region are \(A(3,0)\), E \((\frac{3 }{ 2},\frac{1 }{ 2})\) and \(D(0,2)\).

The values of the objective function of these points are given in following table:

\(\begin{array}{|c|c|c|c|} \hline \text{Point} & \text{x-coordinate} & \text{y-coordinate} & \text{Objective function}~ Z=3 x+5 y \\ \hline A & 3 & 0 & Z_{A}=3 \times 3+5(0)=9 \\ \hline E & \frac{3}{2} & \frac{1}{2} & Z_{E}=3\left(\frac{3}{2}\right)+5\left(\frac{1}{2}\right)=7 \\ \hline D & 0 & 2 & Z_{D}=3(0)+5(2)=10 \\ \hline \end{array}\)

Clearly \(Z\) is minimum at \(x=\frac{3 }{ 2}\) and \(y=\frac{1 }{ 2}\)

Therefore \(x=\frac{3 }{ 2}\) and \(y=\frac{1 }{ 2}\) is the required solution of the L.P. problem and the minimum value of \(Z\) is 7.