Answer: Option 3
Concept:
Quick sort:
- Quicksort is an efficient sorting algorithm also known as a partition-exchange sort
- Quicksort is a comparison sort, meaning that it can sort items of any type for which a "less-than" relation is defined
- Quicksort is a divide-and-conquer algorithm in which the pivot element is chosen, and this pivot element reduced the given problem into two smaller set
- In the efficient implementations, it is not a stable sort, meaning that the relative order of equal sort items is not preserved
- Quicksort can operate in place on an array, requiring small additional amounts of memory to perform the sorting.
In Quicksort, the worst-case takes Θ (n2) time. The worst case of quicksort is when the first or the last element is chosen as the pivot element.
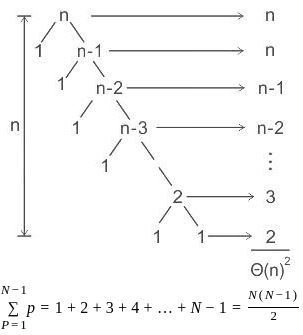
This will give Θ (n2) time complexity.
Recurrence relation for quick sort algorithm will be,
T (n) = T (n - 1) + Θ (n)
This will give the worst-case time complexity as Θ (n2).
Merge sort:
- Merge sort is an efficient sorting algorithm that uses a divide-and-conquer approach to order elements in an array.
- Mergesort has two steps:
- The algorithm uses a divide-and-conquer approach to merge and sort a list.
The recursive mergesort algorithm is
1. If the list has only one element, Return the list and terminate. (Base case)
2. Split the list into two halves that are as equal in length as possible. (Divide)
3. Using recursion, sort both lists using mergesort. (Conquer)
4. Merge the two sorted lists and return the result. (Combine).
In Merge sort, the worst-case takes Θ (n log n) time. Merge sort is based on the divide and conquer approach. It is out of place sorting algorithms
Recurrence relation for merge sort will become:
T(n) = 2T (n/2) + Θ (n)
T(n) = n + Θ (n)
T (n) = n × logn
Selection sort:
Algorithm:
- Find the smallest item in the list, and exchange it with the leftmost unsorted element.
- Repeat the process from the first unsorted element.
Insertion sort:
In Insertion sort, the worst-case takes Θ (n2) time, the worst case of insertion sort is when elements are sorted in reverse order. It is an in-place sorting algorithm.
In that case, the number of comparisons will be like:
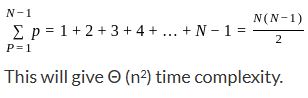


 Get latest Exam Updates
Get latest Exam Updates 
 ×
×
















