Mathematics Test-5

Here, we have to form a 4 digit number lying between 3000 and 5000 using digits 1, 2, 3, 4, 7, 9 such that repetition of digits is allowed.

Unit’s digit can be filled by any one of the given numbers

⇒ No. of ways to fill unit’s digit = 6

Ten’s digit can be filled by any one of the given numbers ⇒ No. of ways to fill ten’s digit = 6

Hundred’s digit can be filled by any one of the given numbers

⇒ No. of ways to fill hundredth digit = 6

Thousand’s digit can be filled by 3 or 4 only

⇒ No. of ways to fill thousand’s digit = 2

∴ The no. of ways to form a 4 digit number lying between 3000 and 5000 using digits 1, 2, 3, 4, 7, 9 such that repetition of digits is allowed = 6 × 6 × 6 × 2 = 432

We know that,

\(\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}\)

\(\cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}\)

\(\sin ^{2} \theta+\cos ^{2} \theta=1\)

\(7 \sin \theta+24 \cos \theta=25\)

Dividing by \(25\) on both the sides, we get

\(\frac{7}{25} \sin \theta+\frac{24}{25} \cos \theta=1 \quad \ldots\) (i)

We know that,

\(\sin ^{2} \theta+\cos ^{2} \theta=1\)

\(\sin \theta \cdot \sin \theta+\cos \theta \cdot \cos \theta=1 \quad \ldots\) (ii)

On comparing equation (i) andequation(ii)

\(\sin \theta=\frac{7}{25}\)

\(\cos \theta=\frac{24}{25}\)

Now, \((\sin \theta+\cos \theta)\)

\(=\frac{7}{25}+\frac{24}{25}\)

\(=\frac{31}{25}\)

We have two vectors \(\vec{a}=5 \hat{i}-\hat{j}+\hat{k}\) and \(\vec{b}=\hat{i}+\hat{j}-\hat{k}\) We know that the angle \(\theta\) between two vectors \(\vec{a}\) and \(\vec{a}\) is:

\(\theta=\cos ^{-1} \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \times|b|} \quad \ldots\) (1)

Therefore,

\(\vec{a} \cdot \vec{b}=(5 \hat{i}-\hat{j}+\hat{k}) \cdot(\hat{i}+\hat{j}-\hat{k})\)

\(\Rightarrow \vec{a} \cdot \vec{b}=5 \hat{i}^{2}+5 \hat{i} \hat{j}-5 \hat{i} \hat{k}-\hat{i} \hat{j}-\hat{j}^{2}+\hat{j} \hat{k}+\hat{i} \hat{k}+\hat{j} \hat{k}-\hat{k}^{2}\)

We know that, \(\left(\hat{i}^{2}=\hat{j}^{2}=\hat{k}^{2}=1\right)\) and \((\hat{i} \hat{j}=\hat{j} \hat{k}=\hat{i} \hat{k}=0)\)

\(\therefore \vec{a} \cdot \vec{b}=5-1-1=3\)

We also know that, if \(\vec{a}=(x \hat{i}+y \hat{j}+z \hat{k})\) then,

\(|\vec{a}|=\sqrt{x^{2}+y^{2}+z^{2}}\)

Therefore, according to the question,

\(\Rightarrow|\vec{a}|=\sqrt{5^{2}+(-1)^{2}+1^{2}}=\sqrt{27}\)

\(\Rightarrow|\vec{b}|=\sqrt{1^{2}+1^{2}+(-1)^{2}}=\sqrt{3}\)

Putting all the above values in equation (1),

\(\Rightarrow \theta=\cos ^{-1} \frac{3}{\sqrt{27} \times \sqrt{3}}\)

\(\Rightarrow \theta=\cos ^{-1} \frac{1}{3}\)

\(\frac{d y}{d x}-y=x, y(0)=0\)

Step size \(=h=0.1\)

Euler's first order formula is

\(y_{1}+1=y_{i}+h f\left(x_{i}, y_{i}\right)\)

\(y_{1}=y_{0}+h f\left(x_{0}, y_{0}\right)\)

Here, \(x_{0}=0, y_{0}=y\left(x_{0}\right)=y(0)=0\)

\(x_{1}=x_{0}+h=0+0.1=0.1\)

\(f(x, y)=\frac{d y}{d x}=y+x\)

\(\Rightarrow y_{1}=y_{0}+h f\left(x_{0}, y_{0}\right)\)

\(=0+0.1 \times f(0,0)\)

\(=0+0.1 \times(0+0)\)

\(=0\)

Now, \(x_{1}=0.1, y_{1}=0\)

\(x_{2}=x_{0}+2 h=0+2 \times 0.1=0.2\)

\(\Rightarrow y_{2}=y_{1}+h f\left(x_{1}, y_{1}\right)\)

\(=0+0.1 \times f(0.1,0)=0+0.1(0.1+0)=0.01\)

Now \(x_{2}=0.2, y_{2}=0.01\)

\(x_{3}=x_{0}+3 h=0+3 \times 0.1=0.3\)

\(\Rightarrow y_{3}=y_{2}+h f\left(x_{2}, y_{2}\right)\)

\(=0.01+0.1 \times f(0.2,0.01)=0.01+0.1(0.2+0.01)=0.031\)

\(\therefore\) at \(x_{3}=0.3, y_{3}=0.031\)

General term: General term in the expansion of \((x+y)^{n}\) is given by

\(T _{( r +1)}={ }^{ n } C _{ r } \times x ^{ n - r } \times y ^{ r }\)

Middle terms: The middle terms is the expansion of \((x+y)^{n}\) depends upon the value of \(n\).

If \(n\) is even, then total number of terms in the expansion of \((x+\) \(y )^{ n }\) is \(n +1\). So there is only one middle term i.e. \(\left(\frac{ n }{2}+1\right)\) th term is the middle term.

If \(n\) is odd, then total number of terms in the expansion of \(( x + y )^{ n }\) is \(n +1\). So there are two middle terms i.e. \(\left(\frac{ n +1}{2}\right)^{\text {th }}\) and \(\left(\frac{ n +3}{2}\right)^{\text {th }}\) are two middle terms.

Here, we have to find the middle terms in the expansion of \(\left(2 x+\frac{1}{x}\right)^{8}\)

Here \(n =8\) ( \(n\) is even number )

Middle term \(=\left(\frac{ n }{2}+1\right)=\left(\frac{8}{2}+1\right)=5\) th term

\(T _{5}= T _{(4+1)}={ }^{8} C _{4} \times(2 x )^{(8-4)} \times\left(\frac{1}{ x }\right)^{4}\)

\(T _{5}={ }^{8} C _{4} \times 2^{4}\)

In this problem, we need to find the point from the option which does not lie which means the point which does not satisfy the equation of the parabola.

To find the equation of parabola:

From question, the parabola formed with the given vertex and focus on positive x axis is:

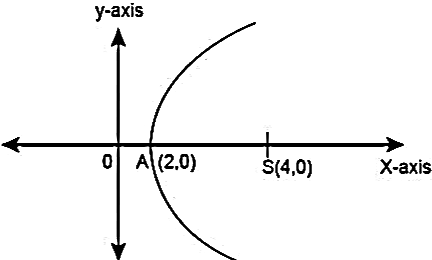
Where,

\({S}=\) Focus

\(A=\) Vertex

The general formula for horizontal parabola is:

\((y-k)^{2}=4 a(x-h)\)

Where,

\((h, k)=\) Vertex

\(a=\) Distance between vertex and focus

Now, from question, we can understand that, \((h, k)=(2,0)\)

Now, ' \(a\) ' is distance between point ' \(A\) ' and 'S'.

The distance between two points is given by the formula:

\(\mathrm{d}=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

On substituting the point ' \(A\) ' and ' \(S\) ',

\(\Rightarrow a=\sqrt{(4-2)^{2}+(0-0)^{2}}\)

\(\Rightarrow a=\sqrt{(2)^{2}}\)

\(\Rightarrow a=\sqrt{4}\)

\(\therefore a=2\)

So, the equation for the given parabola is:

\(\Rightarrow(y-0)^{2}=4 \times 2(x-2)\)

\(\therefore y^{2}=8(x-2)\)

Substituting all the points given in the options:

Option (A):

\((5,2 \sqrt{6}) \Rightarrow({x}, {y})\)

On substituting the point in the obtained parabola equation:

\(\Rightarrow(2 \sqrt{6})^{2}=8(5-2)\)

\(\Rightarrow(4 \times 6)=8(3)\)

\(\Rightarrow 24=24\)

\(\therefore 24-24=0\)

This point satisfies the parabola equation.

Option (B):

\((8,6) \Rightarrow(x, y)\)

On substituting the point in the obtained parabola equation:

\(\Rightarrow(6)^{2}=8(8-2)\)

\(\Rightarrow 36=8(6)\)

\(\therefore 48-36=12\)

This point does not satisfy the parabola equation.

Option (C):

\((6,4 \sqrt{2}) \Rightarrow(x, y)\)

On substituting the point in the obtained parabola equation:

\(\Rightarrow(4 \sqrt{2})^{2}=8(6-2)\)

\(\Rightarrow(16 \times 2)=8(4)\)

\(\Rightarrow 32=32\)

\(\therefore 32-32=0\)

This point satisfies the parabola equation.

Option (D):

\((4,-4) \Rightarrow(x, y)\)

On substituting the point in the obtained parabola equation:

\(\Rightarrow(-4)^{2}=8(4-2)\)

\(\Rightarrow 16=8(2)\)

\(\Rightarrow 16=16\)

\(\therefore 16-16=0\)

This point satisfies the parabola equation.

So, the point which is not satisfying the parabola equation is in option b.

Thus, option (B) does not lie within the parabola.

Given:

\(\Rightarrow f(x)=2^{x}+1\)

\(\Rightarrow f(-3)=2^{-3}+1=\frac{1}{2^{3}}+1\)

\(\Rightarrow f(-3)=\frac{1}{8}+1=\frac{9}{8}\)

\(\Rightarrow f(1)=2+1=3\)

\(\Rightarrow f(3)-1=2^{3}+1-1=8\)

Now, we have \(\frac{9}{8}, 3\) and \(8\)

Clearly, \((3)^{2}=8 \times \frac{9}{8}\)

So, \([f(1)]^{2}=f(-3) \times(f(3)-1)\)

We know, if \(a, b, c\) are in \(G . P\) then \(b^{2}=a c\)

\(\therefore {f}(-3), {f}(1)\) and \(({f}(3)-1)\) are in G.P.

Given: \(2 \cos (\frac{x}{3})+\sqrt{2}=0\)

\(\Rightarrow \cos (\frac{x}{3})=-\frac{\sqrt{2}}{2}=-\frac{1}{\sqrt{2}}\)

As we know that, \(\cos (\frac{\pi}{4})=\frac{1}{\sqrt{2}}\)

\(\Rightarrow \cos (\frac{x}{3})=-\cos (\frac{\pi}{4})=\cos (\pi-(\frac{\pi}{4}))\)

\(\Rightarrow \cos (\frac{x}{3})=\cos (\frac{3\pi}{4})\)

As we know that, if \(\cos \theta=\cos \alpha\) then \(\theta=2 \mathrm{n} \pi \pm \alpha, \alpha \in[0, \pi], {n} \in {Z}\). \(\Rightarrow \frac{x}{3}=2 {n} \pi \pm(\frac{3\pi}{4})\), where \({n} \in {Z}\).

\(\Rightarrow x=6 n \pi \pm(\frac{9\pi}{4})\), where \(n \in Z\).

Given:

\((1+x)^{21}+(1+x)^{22}+\ldots+(1+x)^{30}\)

\(=(1+x)^{21}\left[1+(1+x)^{1}+\ldots+(1+x)^{9}\right]\)

\(=(1+x)^{21}\left[\frac{(1+x)^{10}-1}{(1+x)-1}\right]\)

\(=\frac{1}{x}\left[(1+x)^{31}-(1+x)^{21}\right]\)

\(\therefore\) Coefficient of \(x^{5}\) in the given expression

\(=\) Coefficient of \(x^{5}\) in \(\frac{1}{x}\left[(1+x)^{31}-(1+x)^{21}\right]\)

\(=\) Coefficient of \(x^{6}\) in \(\left[(1+x)^{31}-(1+x)^{21}\right]\)

\(=\) \(^{31} C_{6}-^{21} C_{6}\)

Given complex number is \(Z=-2-i 2 \sqrt{3}\)

\(r \cos \theta=-2, r \sin \theta=-2 \sqrt{3}\)

By squaring and adding, we get,

\(\mathrm{r}^{2}\left(\cos ^{2} \theta+\sin ^{2} \theta\right)=4+12\)

\(\therefore \mathrm{r}=4\)

\(\Rightarrow \cos \theta=\frac{-2}{r}=\frac{-2}{4}=-\frac{1}{2}\) and \(\sin \theta=\frac{-2 \sqrt{3}}{r}=\frac{-2 \sqrt{3}}{4}=-\frac{\sqrt{3}}{2}\)

Since it is in third quadrant \(\theta=-\pi+\frac{\pi}{3}=-\frac{2 \pi}{3}\)

So, on comparing with \(z=r(\cos \theta+i \sin \theta)\), we can write as \(4\left(\cos \left(-\frac{2 \pi}{3}\right)+i \sin \left(-\frac{2 \pi}{3}\right)\right) i \cdot e .4\left(\cos \left(\frac{2 \pi}{3}\right)-i \sin \left(\frac{2 \pi}{3}\right)\right)\).

Let, \(z=\frac{(-\sqrt{3}+3 i)(1-i)}{(3 i-\sqrt{3}) \sqrt{3}(1+i)}\)

\(=\frac{1}{\sqrt{3}}\left(\frac{1-i}{1+i} \times \frac{1-i}{1-i}\right)=-\frac{i}{\sqrt{3}}\)

The complex number \(z\) is represented on \(y\) -axis (imaginary axis)

Meaning of Argand Plane:

Let \(z = a + ib\) be any complex number. If this complex number is represented geometrically by a point \(P\), then the angle made by the line \(OP\) with the real axis is known as argument or amplitude of \(z\) and is expressed as:

Let image of the point \(P(1,3,4)\) is \(Q\) in the given plane.

The equation of the line through \(P\) and normal to the given plane is 

\(\frac{(x-1) }{ 2}=\frac{(y-3) }{-1}=\frac{(z-4) }{ 1}=r\) (say)

Since the line passes through Q. 

So, let the coordinate of \(Q\) are \((2 r+1,-r\) \(+3, r+4)\).

Now, the coordinate of the mid-point of \(P Q\) is \((r+1,-\frac{r }{ 2}+3, \frac{r }{ 2}+4)\).

Now, this point lies in the given plane.

\(2(r+1)-(-\frac{r }{ 2}+3)+(\frac{r }{ 2}+4)+3=0 \)

\(\Rightarrow 2 r+2+\frac{r}{ 2}-3+\frac{r }{ 2}+4+3=0 \)

\(\Rightarrow 3 r+6=0 \)

\(\Rightarrow r=-2\)

So, the coordinate of \(Q\) is \((2 r+1,-r+3, r+4)=(-4+1,2+3,-2+4)\) \(=(-3,5,2)\).

As we know, Standard equation of a circle,

\((x-h)^{2}+(y-k)^{2}=R^{2}\)

Where the center is \((h, k)\) and radius is \(R\).

The distance between a point on a circle and the center is the radius of the circle.

Distance between 2 points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is:

\(D=\sqrt{\left(y_{2}-y_{1}\right)^{2}+\left(x_{2}-x_{1}\right)^{2}}\)

Perpendicular distance of a point \(\left(x_{1}, y_{1}\right)\) from the line \(a x+b y+c=0\),

\(D=\left|\frac{a x_{1}+b y_{1}+c}{\sqrt{a^{2}+b^{2}}}\right|\)

Given, The circle touches the x and y-axis, i.e., the x and y-axis are tangent to the circle.

Equation of the \(x\)-axis is \(y=0\).

Radius is perpendicular distance of centre \(\left(-2,-2\right)\) from the tangent \(\left(y=0\right)\)

Radius \( r=\left|\frac{a x_{1}+b y_{1}+c}{\sqrt{a^{2}+b^{2}}}\right| \)

\(\Rightarrow r=\left|\frac{0 \times(-2)+1 \times(-2)+0}{\sqrt{0^{2}+1^{2}}}\right| \)

\(\Rightarrow r=|-2|=2\)

Equation of circle having centre \(\left(-2,-2\right)\) and radius \(r=2\) is:

\(\left(x-h\right)^{2}+(y-k)^{2}=R^{2} \)

\(\Rightarrow(x-(-2)^{2})+\left(y-(-2)\right)^{2}=2^{2} \)

\(\Rightarrow x^{2}+y^{2}+4 x+4 y+8=4 \)

\(\Rightarrow x^{2}+y^{2}+4 x+4 y+4=0\)

\(P(1,2)\) is mid point of \(A B,\)

Therefore according to figure

Coordinate of \(A\) and \(B\) are \((a,0)\) and \((0,b)\) respectively.

\(\therefore 1=\frac{0+a}{2},2=\frac{0+b}{2}\)

\(\Rightarrow a=2,b=4\)

\(\Rightarrow a=2, b=4\)

\(\Rightarrow A(2,0), B(0,4)\rightarrow\{A(2,0)=A(x_1,y_1), B(0,4)=B(x_2,y_2)\)

Now, Equation of line \(AB\) is

\(y-y_1=m×(x-x_1)\)

Where, \(m=\frac{4-0}{0-2}=-\frac{4}{2}\{{m=\frac{y_2-y_1}{x_2-x_1}}\}\)

\(\Rightarrow y-0=-\frac{4}{2}(x-2)\)

\(\Rightarrow 2x+y=4 \)