Physics Test-5

Planck's constant, dimension is \(=M L^{2} T^{-1}\)

Angular momentum \(=M L^{2} T^{-1}\)

Energy \(=M^{1} L^{2} T^{-2}\)

Mass \(=M^{1} L^{0} T^{0}\)

Frequency \(=M^{0} L^{0} T^{-1}\)

So, Planck's constant has the dimensions of Angular Momentum.

Magnetic Flux \(\phi=\vec{B} \cdot \vec{A}\)

\(\Rightarrow \text { Magnetic flux }(\phi)=\text { B.A.Cos } \theta\)

Given Magnetic Field \(B=\frac{1}{\pi}\left(\frac{{Wb}}{{m}^{2}}\right)\)

Area enclosed \((\) Circular \()=\pi r^{2}\)

\(r=0.2 m\)

Area \(=\pi(0.2)^{2}\)

Angle between field and area \(\theta=60^{\circ}\)

Magnetic Flux \(\phi= \text{B.A.Cos} \theta=\frac{1}{\pi}\left(\frac{W b}{m^{2}}\right)\left(\pi(0.2)^{2}\right)\left(\frac{1}{2}\right)=0.02 Wb\)

Given: Magnetic Flux (\(\phi\)) \(=8 \times 10^{-4} {~Wb}\)

Lenz's Law "The direction of any magnetic induction effect such as to oppose the cause of the effect."

According to Lenz law,

\(e.m.f, |e| =-\frac{d \phi}{d t}\)

\(=-\frac{8 \times 10^{-4}}{0.4}=-2 \times 10^{-3} {V}\)

The lens formula, \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\), gives

\(v=\frac{u f}{u+f}\)......(i)

Differentiate equation (i) w.r.t. time to get the rate of change of image position

\(\frac{{d} v}{{d} t}=\frac{f^{2}}{(u+f)^{2}} \frac{{d} u}{{d} t}\).....(ii)

and differentiate magnification \(m=\frac{v}{u}=\frac{f}{u+d}\)

w.r.t. time to get the rate of change of lateral magnification

\(\frac{{d} m}{{d} t}=-\frac{f}{(u+f)^{2}} \frac{{d} u}{{d} t}\).......(iii)

Substitute \(u=-0.4 {m}\) and \(f=0.3 {m}\)

in equation (i) to get \(v=1.2 {m}\)

Substitute \(\frac{{d} u }{ {d} t}=0.01 {m} / {s}\) in equations (ii) and (iii) to get

\(\frac{{d} v }{{d} t}=0.09 {m} / {s}\)and\(\frac{{d} m}{ {d} t}=-0.3 {s}^{-1}\)

Given: Power \(=+5D\)

When two lenses are separated by some distance \(x\), then equivalent power

\(P=P_{1}+P_{2}-x P_{1} P_{2}\)

\(\therefore P=5+5-x \times 5 \times 5\)

or \(P=10-25 x\)

Power \(P\) will be negative if \(10-25 x\) will be negative

i.e., \(25 x>10\)

or \(x>\frac{10}{25}\)

or \(x>\frac{10}{25} \times 100\) cm

or \(x>40\) cm

Initial Surface Area \(=4 \pi R^{2}\)

\(=4 \pi \left(\frac{\mathrm{D} }{ 2}\right)^{2}\)

\(=\frac{4 \pi D^{2} }{ 4}=\pi D^{2}\)

Surface Area at \(\Delta T\)

\(=4 \pi\left( \frac{\mathrm{D}^{\prime}} {2}\right)^{2}\)

Now

\(D^{\prime}=D(1+\alpha \Delta T)\)

So Surface Area at \(\Delta T\)

\(=4 \pi\left(\frac{\mathrm{D}^{2} }{ 4}\right)(1+\alpha \Delta T)^{2}\)

\(=\pi \mathrm{D}^{2}\left(1+\alpha^{2} \Delta T^{2}+2 \alpha \Delta T\right)\)

Change in surface Area \(=\pi \mathrm{D}^{2}\left(\mathrm{\alpha}^{2} \Delta \mathrm{T}^{2}+2 \alpha \Delta \mathrm{T}\right)\)

\(=\pi \mathrm{D}^{2} \alpha \Delta \mathrm{T}(\alpha \Delta T+2)\)

Basically, a coaxial cable consists of a hollow (outer) cylindrical conductor surrounding a single (inner) conductor along is the axis. The two conductors are well insulated from each other. The electric field (E) and magnetic field (H) at the cross-sections are shown by solid lines and dotted lines, respectively. The outer conductor acts as the shield and minimizes interference.

Different kinds of dielectric materials, such as Teflon and polythene are covered over copper wire, it acts as a spacer. In the transmission of power through coaxial cable, the dielectric medium separating the inner conductor from outer one plays a vital role. These dielectric materials are good insulators only at low frequencies. As the frequency increase, the energy loss becomes significant That is why a coaxial cable can be used effectively for transmission up to a frequency of 20 MHz.

A steady signal flowing in a wire uniformly distributes itself throughout the cross-section of the wire. A high-frequency signal, on the other hand, distributes itself uniformly, there being a concentration of current on the outer surface of the conductor. If the frequency of the current is very high, the current is almost wholly confined to the surface layers. This is called 'Skin effect".

The general condition for Fraunhofer diffraction is \(\frac{b^{2}}{L \lambda} \ll 1\)

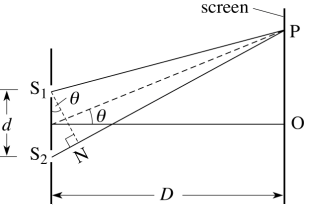
Consider the arrangement of Young's double silt experiment as shown in fig. In which a thin transparent film of refractive index \(\mu\) and thickness t is introduced in front of the lower silt \(S\). Our aim is to obtain the new position of the nth maxima and minima. Let us assume a point \({P}\) on screen at a distance \({Y}\) from the origin \({O}\). It is important to note that in this particular situation cannot calculate the phase difference the two waves arriving at \(P\) directly by calculating the path difference \(\left(S_{2} P-S_{1} P\right)\) because the two waves are not traveling in the same medium. The lower wave travels some distance in a medium ( \(\mu\) ) and the remaining distance in air, while the upper wave travels all the distance in air, in order to calculate the effective path difference we need to convert the distance traveled in medium ( \(\mu\) ) into its equivalent distance air, which is equal to \(\mu\) t and it is called the optical path Hence optical path is the equivalent distance to be traveled in air to produce the same phase change as that produced in actual in traveling the actual distance. Thus, the optical path difference between the two waves is:

\({P}=\left[\left({S}_{2} {P}-{t}\right)+\mu {t}\right]-{S}_{1} {P}\)

or \({P}=\left({S}_{2} {P}-{S}_{1} {P}\right)+(\mu-1) {t}\)

Since \(\quad {S}_{2} {P}-{S}_{1} {P}={d} \sin \theta={d}\left(\frac{{y}^{\prime} }{ {D}}\right) \quad\) (from the fig.)

\(\therefore \quad P=d Y_{n}^{\prime} / D+(\mu-1) t\)

From the nth maxima.

\({P}={n} \lambda,\)

\( \therefore {n} \lambda=\frac{{d} {Y}_{{n}}^{\prime}}{ {D}}+(\mu-1) {t}\) or \({Y}_{{n}}^{\prime}=\frac{{n} \lambda {D}}{ {d}}-(\mu-1) {t} \frac{{D}}{ {d}}\)

For the nth maxima,

\(P=\left(n-\frac{1}{2}\right) \lambda\left(n-\frac{1}{2}\right) \lambda \frac{d y_{2}^{\prime}}{D}+(\mu-1) t\)

or \(Y_{n}^{\prime}=\left(n-\frac{1}{2}\right) \lambda \frac{D}{d}-(\mu-t) \frac{d D}{d}\)

Note that the position of nth maxima and minima has shifted downward by the same distance which is called \({S}={Y}_{{n}}-{Y}_{{n}}^{\prime}=({\mu}-1) \frac{{d} \mathbf{D}}{{d}}\) the fringe shift \(({S})\) and it is given by

The distance between two successive maxima or minima remains unchanged. That is, the fringe width remains unchanged by introducing a transparent flim.

The distance of shift is in the direction where the film is introduced. That is if a film is placed in front of the upper silt \(S_{1},\) the fringe pattern shifts upwards; if a film is placed in front of the lower slit \(\mathrm{S}_{2}\), the fringe pattern shifts downward.

Given: \(R_{1}=5 \mu c i, R_{2}=10 \mu c i, N_{1}=2 N_{2}\)

By, \(\lambda N=R\)

\(\frac{0.693}{T} N=R\)

\(T=\frac{0.693 N}{R}\)

For sample \(S_{1}:\)

\(T_{1}=\frac{0.693 N_{1}}{5}\)

\(T_{1}=\frac{0.693 \times 2 N_{2}}{5}\quad \ldots\) (i)

For sample \(S_{2}\):

\(T_{2}=\frac{0.693 N_{2}}{10} \quad \ldots\) (ii)

By dividing equation (i) by equation(ii), we get:

\(\frac{T_{1}}{T_{2}}=\frac{4}{1}\)

It is clear that the ratio of half-lives of the two samples is \(4:1\), therefore half-lives can be \(20\) \((4k)\) years and \(5\) \((1k)\) years respectively.

Power of a transmitted AM wave is given as:

\(P_{t}=P_{c}\left(1+\frac{\mu^{2}}{2}\right)\)

\(P_{t}=P_{c}+P_{c} \frac{\mu^{2}}{2}\)

Power in the carrier \(=P_{c}\)

Power in both the sidebands is given by:

\(P_{s 1}=\frac{P_{c} u^{2}}{4}\)

We know that:

\(P_{t}=P_{c}\left(1+\frac{\mu^{2}}{2}\right)\)

\(2.09=P_{c}\left(1+\frac{0.09}{2}\right)\)

\(\therefore P_{c}=2\) Watts

Power in each sideband is,

\(P_{S B}=P_{c} \frac{\mu^{2}}{4}=\frac{2(0.09)}{4}\)

\(=0.045\) Watts

Before impact, the velocity is given by \(u_{1}=\sqrt{2 g h}\)

The initial and final velocity of the surface will be Zero

After the first impact \(e=\frac{\left|\left(0-v_{1}\right)\right|}{\left|\left(u_{1}-0\right)\right|}=\frac{v_{1}}{u_{1}}\)

\(e=\frac{\sqrt{2 g h_{1}}}{\sqrt{2 g h}}=\sqrt{\frac{h_{1}}{h}}\)

\(h_{1}=e^{2} h\)

Now after the second impact

\(v_{1}=\sqrt{2 g e^{2} h}\)

\(v_{2}=\sqrt{2 g h_{2}}\)

\(e=\frac{\left|\left(0-v_{2}\right)\right|}{\left|\left(v_{1}-0\right)\right|}=\frac{v_{2}}{v_{1}}=\sqrt{\frac{2 g h_{2}}{2 g e^{2} h}}\)

\(h_{2}=e^{2} e^{2} h=e^{4} h\).

Refractive index (μ): The ratio of the velocity of light in vacuum to the velocity of light in the medium is called refractive index of that medium.

The refractive index of a substance/medium \(=\frac{\text { Velocity of light in vacuum }}{\text { Velocity of light in the medium }}\)

So \(\mu= \frac{c}{v}\)

Where \(c\) is the speed of light in vacuum and \(v\) is the speed of light in the medium.

Given:

Refractive index of the diamond \(\left(\mu_{ d }\right)=2.5\)

We know that,

The velocity of light in vacuum \(( c )=3 \times 10^{8} m / s\)

To find the velocity of light in diamond (v)

Now,

\(\mu_{d}=\frac{c}{v}\) or, \(2.5=\frac{3 \times 10^{8}}{v}\) or,\(v=\frac{3 \times 10^{8}}{2.5}=1.2 \times 10^{8} m / s\)

Given,

\(\Delta C _{ P }=2.0+0.2 T cal / deg\)

\((\Delta H )_{\text {reac }}\) at \(10 K =-14.38 K cal\)

By Kirchoff's equation,

\(\frac{\Delta H _{2}-\Delta H _{1}}{ T _{2}- T _{1}}=\Delta C _{ P }\)

\(\Rightarrow \Delta H _{2}-\Delta H _{1}=\int_{ T _{1}}^{ T _{2}} \Delta C _{ P } dT\)

\(\Rightarrow \Delta H _{2}-\Delta H _{1}=\int_{10 K }^{100 K }(2.0+0.2 T ) dT\)

\(\Rightarrow \Delta H _{2}-\Delta H _{1}=\left[2 T +0.1 T ^{2}\right]_{10}^{100}\)

\(\Rightarrow \Delta H _{2}-\Delta H _{1}=2(100-10)+0.1\left(100^{2}-10^{2}\right)\)

\(\Rightarrow \Delta H _{2}-\Delta H _{1}=180+0.1 \times 110 \times 90\)

\(\Rightarrow \Delta H _{2}-\Delta H _{1}=180+990=1.170 Kcal\)

\(\Rightarrow \Delta H _{2}=\Delta H _{1}+1 \cdot 170\)

\(=-14.38+1.17\)

\(\Delta H _{2}=-13.21 K cal\)

\(\therefore\) Enthalpy of reaction at \(100 K\) in \(K\) cal will be \(-13.21 K\) cal.

The electric current of an electromagnet is switched off then the magnetic property of the electromagnet will remain for few moment.

An electromagnet is a temporary magnet which should ideally have the property to behave as a magnet when current passes through it and lose magnetism as soon as current is stopped.

Soft iron is generally used for making electromagnets because it has high magnetic permeability, i.e. it can easily gain magnetic properties when current is passed around the core and quickly lose when current is stopped.

The soft iron inside the coil makes the magnetic field stronger because it becomes a magnet itself when the current is flowing.