Physics Test - 45

Given,

Acceleration, \(a=2 \mathrm{~m} / \mathrm{s}^{2}\)

\(u=20 \mathrm{~m} / \mathrm{s}\)

\(v=30 \mathrm{~m} / \mathrm{s}\)

From equation of motion,

\(v^{2}-u^{2}=2 a s\)

\(\Rightarrow s=\frac{\left(v^{2}-u^{2}\right) }{(2 \times a)}\)

\(\Rightarrow s=\frac{\left(30^{2}-20^{2}\right) }{(2 \times 2)}\)

\(\Rightarrow s=\frac{500 } 4\)

\(\Rightarrow s=125 ~m\)

Given:

Radius of wire\(=10 cm\)

Magnetic field \(=100 T\)

Time \(=0.1 s\)

Average induced emf in loop,

\(2 \pi R=4 L\)

Therefore,

\(L=\frac{\pi R}{2}\)

\(\Rightarrow \pi \times \frac{10}{2}=5 \pi cm\)

\(\Delta s=S i-S f\)

\(\Rightarrow \pi r^{2}-L^{2}\)

\(=\pi(0.1)^{2}-(5 \pi)^{2} \times 10^{\circ} 4\)

\(=0.0067\)

Now,

\(e=\frac{\Delta \Phi}{\Delta t}\)

\(\Rightarrow \frac{B.\Delta s}{\Delta t}=100 \times \frac{0.0067}{0.1}\)

\(=6.7 V\)

Let us assume that the charge \(q=\ 10 \mu C=10^{-5} C\) is placed at a distance of \(5 cm\) from the square \(A B C D\) of each side \(10 cm\). The square \(A B C D\) can be considered as one of the six faces of a cubic Gaussian surface of each side \(10 cm\).

Now, the total electric flux through the faces of the cube as per Gaussian theorem:

\(\phi=\frac{q}{\epsilon_{0}}\)

Therefore, the total electric flux through the square \(A B C D\) will be:

\(\phi_{E}=\frac{1}{6} \times \phi\)

\(=\frac{1}{6} \times \frac{q}{\epsilon_{0}} \)

\(=\frac{1}{6} \times \frac{10^{-5}}{8.854 \times 10^{-12}} \quad\left(\because \epsilon_{0}=8.854 \times 10^{-12}\right) \)

\(=1.88 \times 10^{5} Nm ^{2} C ^{-1}\)

Ferromagnetic substances are those which gets strongly magnetised whenplaced in an external magnetic field. They have strong tendency to movefrom a region of weak magnetic field to strong magnetic field, i.e., they getstrongly attracted to a magnet.

The individual atoms (or ions or molecules) in a ferromagnetic materialpossess a dipole moment as in a paramagnetic material. However, theyinteract with one another in such a way that they spontaneously alignthemselves in a common direction over a macroscopic volume calleddomain.

Given,

Length of the rod \(=1\)

Linear charge density of the rod, \(\rho(x)=\rho_{0}\left(\frac{x}{l}\right)\)

Rotations per second \(=\mathrm{n}\)

A rotating charge constitutes a current. Hence, a rotating charged rod behaves like a current carrying coil.

If charge q rotates with a frequency \(\mathrm{n}\), then equivalent current is \(\mathrm{I}=\mathrm{qn}\)

Magnetic moment associated with this current is \(\mathrm{M}=\mathrm{IA}\).

Where, \(\mathrm{A}=\) area of coil or area swept by rotating rod.

Let dq be the charge on \(\mathrm{dx}\) length of rod at a distance \(\mathrm{x}\) from origin as shown in the figure below.

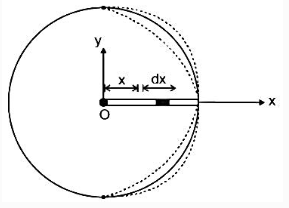
The magnetic moment \(d m\) of this portion \(\mathrm{dx}\) is given as

\(\Rightarrow \mathrm{dm}=(\mathrm{dl}) \mathrm{A}\)

\(\because[I=q n \Rightarrow d \mid=n d q]\)

\(\Rightarrow \mathrm{dm}=\mathrm{ndqA}\)

\(\Rightarrow \mathrm{dm}=\mathrm{n} \lambda \mathrm{dxA}\)

Where, \(\lambda=\) charge density of rod \(=\rho(x)=\rho_{0} \frac{x}{l}\)

So,

\(\Rightarrow d m=\frac{n \rho_{0} x d x \pi x^{2}}{l}=\frac{\pi n \rho_{0}}{l} x^{3} d x\)

Here,

Area \(\mathrm{A}=\pi r^{2}=\pi \mathrm{x}^{2}\)

Total magnetic moment associated with rotating rod is sum of all the magnetic moments of differentiable elements of rod.

So, magnetic moment associated with complete rod is

\(\Rightarrow M=\int_{x=0}^{x=l} d m\)

\(\Rightarrow M=\int_{0}^{l} \frac{\pi n \rho_{0}}{l} \cdot x^{3} d x\)

\(\Rightarrow M=\frac{\pi n \rho_{0}}{l} \cdot \int_{0}^{l} x^{3} d x\)

\(\Rightarrow M=\frac{\pi n \rho_{0}}{l}\left[\frac{x^{4}}{4}\right]_{0}^{l}\)

\(\Rightarrow M=\frac{\pi n \rho_{0}}{l}\left[\frac{l^{4}}{4}\right]\)

\(\Rightarrow M=\frac{\pi n \rho_{0} l^{3}}{4}\)

At \(\rho_{0}=\rho\)

\(\Rightarrow M=\frac{\pi n \rho x l^{2}}{4}\)

At \(x=1\)

\(\therefore M=\frac{\pi}{4} n \rho l^{3}\)

Applying conservation of momentum,

\(m _{1} v _{1}= m _{2} v _{2}\)

\(\Rightarrow \rho \frac{4}{3} \pi r_{1}^{3} v_{1}=\rho \frac{4}{3} \pi r_{2}^{3} v_{2}\)

\(\Rightarrow r_{1}^{3} v_{1}=r_{2}^{3} v_{2}\)

\(\Rightarrow \frac{v_{1}}{v_{2}}=\left(\frac{r_{2}}{r_{1}}\right)^{3}\)

\(\Rightarrow \frac{v_{1}}{v_{2}}=(\frac 21)^{3}\)

\(\Rightarrow \frac{v_{1}}{v_{2}}=\frac 81\)

or \(8:1\)

When the two equi-convex lenses are in contact with each other the power of the lenses is directly added and the space present in between the two lenses is like a concave lens so glycerine is in the form of a diverging lens.

The image of the equi-convex lenses are in contact with each other and the image of adding glycerine in between them is shown below;

To calculate the power we have two cases one \(P_1\) is the combination of the power of the equi-convex lens and the second \(P _2\) is the power of glycerine added and forming the diverging lens.

As we know that power is the reciprocal of the focal length.

Now, for the first case, the power of the equi-convex lens is written as,

Where, \(P =\frac{1}{f} \dots\) (1)

Now, on putting these values of \(P\) in equation (1) we have;

\(\frac{1}{F_1}=\frac{1}{f}+\frac{1}{f}=\frac{2}{f} \)

\(\Rightarrow F_1=\frac{f}{2}\dots\) (2)

When glycerin is filled inside, the glycerin lens behaves like a diverging lens of focal length \((-f)\) and power \(P _2\) is written as;

\(P_2=P+P+(-P)\)

Where, \(P =\frac{1}{f}\)

\(\Rightarrow \frac{1}{F_2}=\frac{1}{f}+\frac{1}{f}-\frac{1}{f} \)

\( F_2=f\dots\) (3)

Now, on dividing equation (2) by equation (3), we get;

\(\frac{F_1}{F_2}=\frac{1}{2}\)

For (A)

\(x_P-x_Q=(d+2.5)-(d-2.5)=5 m\)

Phase difference \(\Delta \phi\) due to path difference

\(=\frac{2 \pi}{\lambda}(\Delta \mathrm{x})=\frac{2 \pi}{20}(5)=\frac{\pi}{2}\)

At A, Q is ahead of \(\mathrm{P}\) by path, as wave emitted by \(\mathrm{Q}\) reaches before wave emitted by \(P\).

\(\therefore\) Total phase difference at \(\mathrm{A} \frac{\pi}{2}-\frac{\pi}{2}=0\)

(due to \(\mathrm{P}\) being ahead of \(\mathrm{Q}\) by \(90^{\circ}\) )

\(I_A=I_1+I_2+2 \sqrt{I_1} \sqrt{I_2} \cos \Delta \phi \)

\(=I+I+2 \sqrt{I} \sqrt{I} \cos (0)=4 I\)

For C

Path difference, \(\mathrm{x}_{\mathrm{Q}}-\mathrm{x}_{\mathrm{P}}=5 \mathrm{~m}\)

Phase difference \(\Delta \phi\) due to path difference

\(=\frac{2 \pi}{\lambda}(\Delta \mathrm{x})=\frac{2 \pi}{20}(5)=\frac{\pi}{2}\)

Total phase difference at \(\mathrm{C}=\frac{\pi}{2}+\frac{\pi}{2}=\pi\)

\(I_{\text {net }}=I_1+I_2+2 \sqrt{I_1} \sqrt{I_2} \cos (\Delta \phi) \)

\(=I+I+2 \sqrt{I} \sqrt{I} \cos (\pi)=0\)

For B,

Path difference, \(\mathrm{x}_{\mathrm{P}}-\mathrm{x}_{\mathrm{O}}=0\)

Phase difference, \(\Delta \phi=\frac{\pi}{2}\)

(due to \(\mathrm{P}\) being ahead of \(\mathrm{Q}\) by \(90^{\circ}\) )

\(I_B=I+I+2 \sqrt{I} \sqrt{I} \cos \frac{\pi}{2}=2 I\)

Therefore intensities of radiation at \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\) will be in the ratio

\(\mathrm{I}_{\mathrm{A}}: \mathrm{I}_{\mathrm{B}}: \mathrm{I}_{\mathrm{C}}=4 \mathrm{I}: 2 \mathrm{I}: 0=2: 1: 0\)

Let the work function for the given metal be \(\phi\). When the light of the frequency \(n\) falls on the surface of the metal, the maximum kinetic energy of the ejected photoelectron is given by,

\(K . E_{\max }=n h-\phi\)

\(\frac{1}{2} m v^{2}=n h-\phi \quad \ldots(i)\)

When the light of the frequency 3n falls on the surface of the metal, the maximum kinetic energy of the ejected photoelectron is given by,

\(K . E_{\max }=3 n h-\phi\)

Let the maximum velocity of the electron be \(v\). 

\(\frac{1}{2} m v^{2}=3 n h-\phi \quad \ldots(i i)\)

Substituting \(n h=\frac{1}{2} m v^{2}+\phi\) from equation (i) to equation (ii) 

\(\frac{1}{2} m v^{2}=3\left(\frac{1}{2} m v^{2}+\phi\right)-\phi\)

\(\frac{1}{2} m v^{2}=\frac{3}{2} m v^{2}\)

\(\frac{1}{2} m v^{2}-\frac{3}{2} m v^{2}=0\)

The work function cannot be negative or zero.

Thus, \(\frac{1}{2} m v^{2}-\frac{3}{2} m v^{2}>0\)

\(\frac{1}{2} m v^2>\frac{3}{2} m v^2\)

\(\Rightarrow v >v \sqrt{3}\)

When a point charge \(+\mathrm{q}\) is placed at a distance (\(\mathrm{d}\)) from an isolated conducting plane, some negative charge develops on the surface of the plane towards the charge and an equal positive charge develops on the opposite side of the plane. Hence, the field at a point \(\mathrm{P}\) on the other side of the plane is directed perpendicular to the plane and away from the plane as shown in figure: