CBSE 10th Term-2 2022 : Maths Important Short Answer Type Questions (3 Marks)

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
CBSE 10th Term-2 2022 : Maths Important Short Answer Type Questions (3 Marks)
These questions are suggested by the experts for the upcoming Term 2 Exam. Students must practice all these questions to improve their preparation level so that they can score good marks in their Maths Term 2 Exam 2022. All important questions can be read in this article.
| CBSE Class 10 Term 2 Maths Study Material | |
| CBSE Class 12 Maths Term 2 Syllabus | CBSE Class 12 Maths Term 2 Sample Paper Set Wise |
| CBSE Class 12 Term 2 Study Material | CBSE Class 12 Full Study Material |
CBSE Class 10 Maths Important 3 marks Questions from chapters are provided below.
Chapter
Quadratic Equations
Q.1. Find two consecutive positive integers, the sum of whose squares is 365.
Ans. Let the first integer be x.
The next consecutive positive integer will be x + 1.
According to the given question,
x² + ( x + 1)² = 365
x² +( x + 1)² = 365
x² + (x² + 2x + 1) = 365 [ ∵ (a + b)² = a² + 2ab + b²]
2x² + 2x + 1 = 365
2x² + 2x + 1- 365 = 0
2x² + 2x - 364 = 0
2(x² + x - 182) = 0
x² + x - 182 = 0
x² + 14x - 13x - 182 = 0
x (x + 14) - 13 (x + 14) = 0
(x - 13) (x + 14) = 0
x - 13 = 0 and x + 14 = 0
x = 13 and x = - 14
The value of x cannot be negative (because it is given that the integers are positive).
∴ x = 13 and x + 1 = 14
Q.2. If 2 is a root of the equation x2 + bx +12 =0, find the value of b.
Ans. Since 2 is a root of the equation,
Therefore, x=2 should satisfy the equation
Therefore 2² + b×2 + 12 = 0
4 + 2b + 12 = 0
16 + 2b = 0
2b = -16
b = -16/2
b = -8
Q.3. Find two numbers whose sum is 27 and product is 182.
Ans. Let us assume,
The first number as x
The second number as 27 – x.
Hence, the product of two numbers
x(27 – x) = 182
⇒ x2 – 27x – 182 = 0
⇒ x2 – 13x – 14x + 182 = 0
⇒ x(x – 13) -14(x – 13) = 0
⇒ (x – 13)(x -14) = 0
Thus, x = -13 = 0 or x – 14 = 0
⇒ x = 13 or x = 14
Hence, if first number = 13, then second number = 27 – 13 = 14
And if first number = 14, then second number = 27 – 14 = 13
Q.4. Find the roots of x + 1/x = 3; x ≠ 0.
Ans. Given,
x + 1/x = 3; x ≠ 0
(x2 + 1)/x = 3
x2 + 1 = 3x
x2 – 3x + 1 = 0
Comparing with the standard form ax2 + bx + c = 0,
a = 1, b = -3, c = 1
Using quadratic formula,
x = [-b ± √(b2 – 4ac)]/2a
= [-(-3) ± √{(-3)2 – 4(1)(1)}]/2(1)
= [3 ± √(9 – 4)]/2
= (3 ± √5)/2
Therefore, (3 + √5)/2 and (3 – √5)/2 are the roots of given equation.
Q.5. Find the roots of the quadratic equation: 3x2 - 2√6x + 2 = 0
Ans.

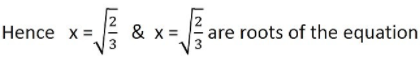
Q.6. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13cm, find the other two sides.
Ans. Let us consider, the base of the right triangle be x cm.
The altitude of right triangle = (x – 7) cm
From Pythagoras theorem, we know,
Base2 + Altitude2 = Hypotenuse2
∴ x2 + (x – 7)2 = 132
⇒ x2 + x2 + 49 – 14x = 169
⇒ 2x2 – 14x – 120 = 0
⇒ x2 – 7x – 60 = 0
⇒ x2 – 12x + 5x – 60 = 0
⇒ x(x – 12) + 5(x – 12) = 0
⇒ (x – 12)(x + 5) = 0
Thus, either x – 12 = 0 or x + 5 = 0,
⇒ x = 12 or x = – 5
Since sides cannot be negative, x can only be 12.
Hence, the base of the given triangle is 12 cm
The altitude of this triangle will be (12 – 7) cm = 5 cm.
Q.7. Find the value of p, for which one root of the quadratic equation px2 – 14x + 8 = 0 is 6 times the other
Ans. Given, equation is px2 − 14x + 8 = 0
Let one root = α then other root = 6 α
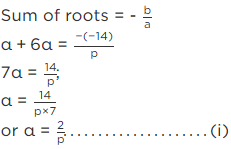
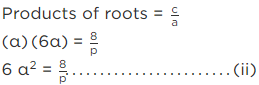
Putting value of α from eq.(i)
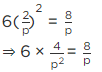
⇒ 24p = 8p2
⇒ 8p2 − 24p = 0
⇒ 8p (p−3) = 0
⇒ Either 8p = 0 ⇒ p = 0
⇒ p − 3 = 0 ⇒ p = 3
For p = 0, given condition is not satisfied [∵ leading coefficient can't be zero].
∴ p = 3
Q.8. Find the value of k for which the following equation has equal roots:
(k - 12)x2 + 2(k - 12)x + 2 = 0.
Ans. The given equation is
(k - 12)x2 + 2(k - 12)x + 2 = 0
Here, a = k - 12, b = 2(k - 12) and c = 2
Since, the given equation has two equal real roots
then we must have b2 - 4ac = 0
⇒ [2(k - 12)]2 - 4(k - 12) x 2 = 0
⇒ 4(k - 12)2 - 8(k - 12) = 0
⇒ 4(k - 12) {k - 12 - 2} = 0
⇒ (k - 12) (k - 14) = 0
⇒ k - 12 = 0 or k - 14 = 0
⇒ k = 12 or k = 14.
Note: But at k = 12, terms of x2 and x in the equation vanish hence only k = 14 is acceptable.
Q.9. Find the discriminant of the equation 3x2 – 2x +1/3= 0 and hence find the nature of its roots. Find them, if they are real.
Ans. Here a = 3, b = – 2 and c=1/3.
Therefore, discriminant b2 – 4ac = (– 2)2 – 4 × 3 ×1/3 = 4 – 4 = 0.
Hence, the given quadratic equation has two equal real roots.
The roots are
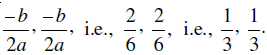
Q.10. Three consecutive natural numbers are such that the square of the middle number exceeds the difference of squares of the other, two by 60. Find the numbers.
Ans.
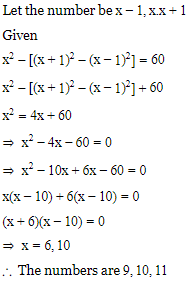
Chapter
Arithmetic Progressions
Q.1. If the 3rd and the 9th term of an AP are 4 and -8 respectively, which term of this AP is zero?
Ans. Given that,
a3 = 4
a9 = −8
We know that,
an = a + (n − 1) d
a3 = a + (3 − 1) d
4 = a + 2d (I)
a9 = a + (9 − 1) d
−8 = a + 8d (II)
On subtracting equation (I) from (II), we obtain
−12 = 6d
d = −2
From equation (I), we obtain
4 = a + 2 (−2)
4 = a − 4
a = 8
Let nth term of this A.P. be zero.
an = a + (n − 1) d
0 = 8 + (n − 1) (−2)
0 = 8 − 2n + 2
2n = 10
n = 5
Hence, 5th term of this A.P. is 0.
Q.2. If (3y – 1), (3y + 5) and (5y + 1) are three consecutive terms of an AP then find the value of y.
Ans. It is given that (3y - 1),(3y +5) and (5y +1) are three consecutive terms of an AP.
∴ (3y +5 ) -(3y-1) = (5y+1) -(3y+5)
⇒ 3y +5-3y +1 = 5y +1 -3y -5
⇒ 6 = 2y - 4
⇒ 2y = 6+4 =10
⇒ y = 5
Hence, the value of y is 5.
Q.3. The fifth term of an A.P is 20 and the sum of its seventh and eleventh terms is 64. Find the Common Difference.
Ans. Let the first term of AP be a and common difference be d,
According to question,
5th term is 20 => a+4d=20 .......(1)
And, a+6d+a+10d=64
=> 2a+16d=64
=> a+8d=32 .........(2)
From (1) & (2),
d=3, & a=8
Hence common Difference= 3
Q.4. Find if 100 is the term of A.P. 25,28,31...or not.
Ans. Formula,
Tn = a + (n−1)d
Given,
100 = 25 + (n−1)3
75 = 3n − 3
n = 378 = 26
100 is the 26th term.
Q.5. How many two-digit natural numbers are divisible by 7?
Ans. The 2-digit number divisible by 7 is 14, 21, 28, 35……98
The first 2-digit number which is divisible by 7 is 14
The last 2-digit number which is divisible by 7 is 98
The list of 2-digit numbers divisible by 7 are
14, 21, 28, 35……98 which forms an A.P
Consider a formula
T(n) = a + (n – 1)d
Where
a = 14
d = 7
T(n) = 98
98 = 14 + (n – 1)7
84 = 7n – 7
7n = 91
n = 13
∴ There are 13 two – digits number which are divisible by 7.
Q.6. If the ratio of the sum of first n terms of two A.P.'s is (7n+1): (4n+27), find the ratio of their mth terms.
Ans. Let a1, a2 be the first terms and d1, d2 the common differences of the two given A.P.'s. Then, the sums of their n terms are given by
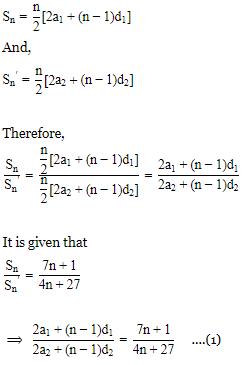
To find the ratio of the mth terms of the two given AP's, we replace n by (2m-1) in equation 1.
Therefore,
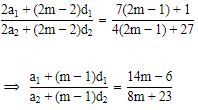
Hence, the ratio of the mth terms of two AP's is (14m − 6) : (8m + 23).
Q.7. Find the sum of all odd numbers between 0 and 50.
Ans. Odd numbers are classified as any number that is not divisible by two. In other terms, a number in the form of 2k+1, where k ∈ integers(Z) are called odd numbers. The sum of two odd numbers is always even.
The list of odd numbers between 0 and 50 are
1,3, 5, 7, 9, ….49.
To find the sum of all the odd numbers between 0 – 50 we use the theory of arithmetic progression.
a = 1
d = 2
n = ?
Tn = 49
Tn = a + (n-1)d
49 = 1 + (n – 1) × 2
49 = 1 + 2n – 2
49 = 2n -1
50 = 2n
n = 25
The sum of all odd numbers between 0 and 50 can be calculated using the formula
Sn = n/2 (a +Tn)
Sn = 25/2 (1 + 49)
Sn = 25/2 (50)
Sn = 625
Q.8. If mth term of an AP is 1/n and nth term is 1/m then find the sum of its first mn terms.
Ans. Let a be first term and d be the common difference of an AP.
mth term=1/n
so,
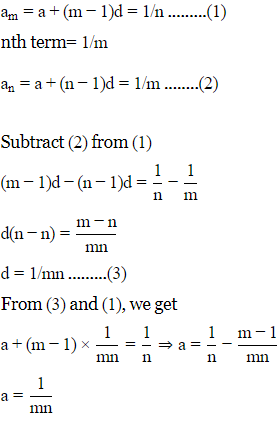
Sum of first k terms = (k/2) [2a+ (k−1) d]
Smn = mn/2[2(1/mn)+(mn−1)(1/mn)]
= mn/2[1/mn+1]
= (1+mn)/2.
Q.9. How many terms of the A.P: 24, 21, 18, ……… must be taken so that their sum is 78?
Ans. Let the number of terms taken be n.
THe given A.P is 24, 21, 18, .....
Here a = 24 and d = 21 - 24= -3
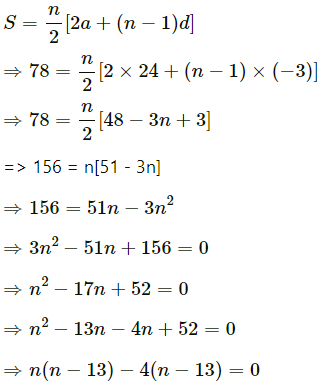
=> n = 13 or n = 4
∴ Required number of term = 4 or 13
Q.10. Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
Ans. Since, the number is divisible by both 2 and 5, means it must be divisible by 10.
In the given numbers, first number that is divisible by 10 is 110.
Next number is 110 + 10 = 120.
The last number that is divisible by 10 is 990.
Thus, the progression will be 110, 120, ..., 990.
All the terms are divisible by 10, and thus forms an A.P. having first term as 110 and the common difference as 10.
We know that, nth term = an = a + (n − 1)d
According to the question,
990 = 110 + (n − 1)10
⇒ 990 = 110 + 10n − 10
⇒ 10n = 990 − 100
⇒ 10n = 890
⇒ n = 89
Thus, the number of natural numbers between 101 and 999 which are divisible by both 2 and 5 is 89.
Chapter
Circles
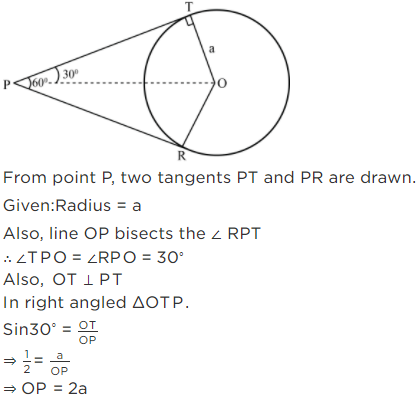
Q.1. If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60∘ , then OP = a√3.
Ans. False
Q.2. In Figure , common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB = CD.
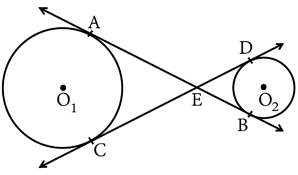
Ans. From the given figure, AB and CD are common tangents on both the circles. AB and CD intersect at E.
Now, EA=EC (Tangents drawn on circle from same point)
EB = ED (Tangents drawn on circle from same point)
EA + EB = EC + ED
AB = CD
Q.3. If all the sides of a parallelogram touch a circle, show that the parallelogram is a rhombus.
Ans.
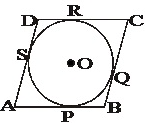
Let ABCD be a parallelogram whose sides AB, BC, CD and DA touch a circle at the points P, Q, R and S respectively.
Since the lengths of tangents drawn from an external point to a circle are equal, we have
AP = AS, BP = BQ, CR = CQ and DR = DS.
AB + CD = AP + BP + CR + DR
= AS + BQ + CQ + DS
= (AS + DS) + (BQ+CQ)
= AD + BC
Now, AB + CD = AD + BC
⇒ 2AB = 2BC
⇒ AB = BC
AB = BC = CD = AD.
Hence, ABCD is a rhombus.
Q.4. XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠AOB = 90∘.
Ans.
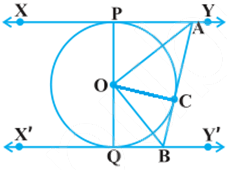
We joined O and C.
According to question,
In Δ OPA and Δ OCA,
OP = OC (Radii of the same circle)
AP = AC (Tangents from point A)
AO = AO (Common side)
∴ΔOPA ≅ ΔOCA (SSS congruence criterion)
⇒ ∠POA = ∠COA … (i)
Similarly,
ΔOQB ≅ ΔOCB
∠QOB = ∠COB … (ii)
Since POQ is a diameter of the circle, it is a straight line.
∴ ∠POA + ∠COA + ∠COB + ∠QOB = 180∘
From equations (i) and (ii),
2∠COA + 2∠COB = 180∘
⇒ ∠COA + ∠COB = 90∘
⇒ ∠AOB = 90∘
Q.5. A circle is inscribed in a quadrilateral ABCD in which ∠B=90∘. If AD = 23 cm, AB = 29 cm and DS = cm, find the radius r of the circle.
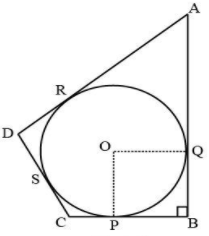
Ans.
∠B=90∘
Given : ABCD is a quadrilateral in which ∠B=90∘, AD = 23 cm, DS = 5 cm and AB = 29 cm
Let radius of the incircle be r cm.
RD = DS = 5cm (Tangents from an external point)
∵ AD = 23cm
So,
AR + RD = AD
⇒ AR + 5 = 23cm
⇒ AR = 18cm (i)
And,
AQ = AR (Tangents from an external point)
∵ AR = 18 cm from(i)
So,
AQ + QB = AB
⇒ 18 + QB = 29cm
⇒ QB = 11cm
Now, OP and OQ are radius of the circle. So,
From tangents P and Q,
∠OPB=∠OQB = 90∘
⇒ OPBQ is a square (all angles are right angle)
⇒ OP = QB
⇒ Radius of the circle (r) = QB = 11cm
Hence, radius of the circle is 11 cm.
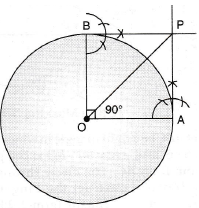
Q.6. In fig., tangent segments PS and PT are drawn to a circle with centre O such that ∠SPT = 120o. Prove that OP = 2 PS.
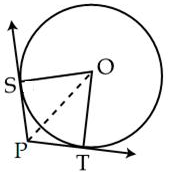
Ans. Tangents drawn from an external point to the circle are equal.
∴ PS = PT
Radius is perpendicular to the tangent at the point of contact.

Q.7. In fig.3 PQ and PR are tangents to the circle with centre O and S is a point on the circle such that ∠SQL = 50∘ and ∠SRM = 60∘. Find ∠QSR.
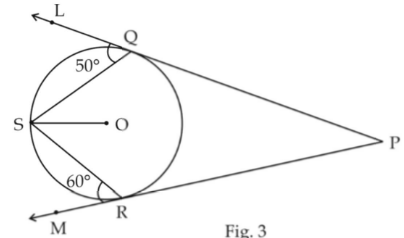
Ans.
Q.8. Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
Ans. Given: A circle with centre O and an external point T from which tangents TP and TQ are drawn to touch the circle at P and Q.
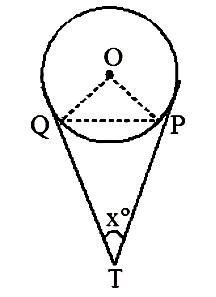
To prove: ∠PTQ = 2∠OPQ.
Proof: Let ∠PTQ = xº. Then,
∠TQP + ∠TPQ + ∠PTQ = 180º
[∵ sum of the ∠s of a triangle is 180º]
⇒ ∠TQP + ∠TPQ = (180º – x) ….(i)
We know that the lengths of tangent drawn from an external point to a circle are equal.
So, TP = TQ.
Now, TP = TQ
⇒ ∠TQP = ∠TPQ
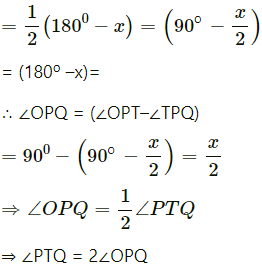
Q.9. In figure, OP is equal to diameter of the circle. Prove that ABP is a equilateral triangle
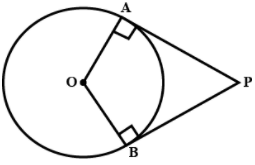
Ans. PA and PB are the tangents to the circle.
∴ OA ⊥ PA
⇒ ∠OAP=90°
In ΔOPA,

⇒ sin∠OPA = 2/1 = sin30⁰
⇒ ∠OPA = 30°
Similarly, it can be proved that ∠OPB = 30°.
Now, ∠APB = ∠OPA + ∠OPB = 30° + 30° = 60°
In ΔPAB,
PA = PB [lengths of tangents drawn from an external point to a circle are equal]
⇒ ∠PAB = ∠PBA ............(1) [Equal sides have equal angles opposite to them]
∠PAB + ∠PBA + ∠APB = 180° [Angle sum property]
⇒ ∠PAB + ∠PAB = 180° – 60° = 120° [Using (1)]
⇒ 2 ∠PAB = 120°
⇒ ∠PAB = 60° .............(2)
From (1) and (2)
∠PAB = ∠PBA = ∠APB = 60°
∴ ΔPAB is an equilateral triangle.
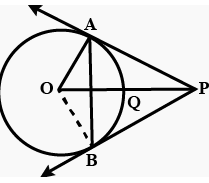
Q.10. In given figure, chords AB and CD of a circleintersect at P. If AB = 5 cm, PB = 3 cm and PD = 4 cm, then find the length of CD.
Ans. Here chords AB and CD of a circle intersect at P.
AB = 5 cm, PB = 3 cm and PD = 4 cm, CD = ?
Let us assume CD = x
We know that if chords AB and CD intersect externally at point P then
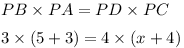
24 = 4x+16
4x = 24-16
4x = 8
x = 2 cm
Therefore, CD = 2 cm.
Chapter
Constructions
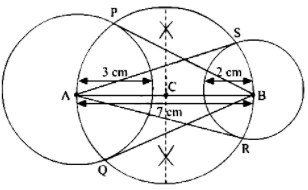
Q.1. Draw a line segment AB of length 7 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle.
Ans. Steps of Construction
Step 1: Draw a line segment AB = 7 cm.
Step 2: With centre A and radius 3 cm, draw a circle.
Step 3: With centre B and radius 2 cm, draw a circle.
Step 4: Bisect the line AB. Let the mid-point of AB be C.
Step 5: Taking C as centre, draw a circle with AC as radius that intersect the circles at points P, Q, R and S.
Step 6: Join BP, BQ, AS and AR.
Q.2. Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
Ans.
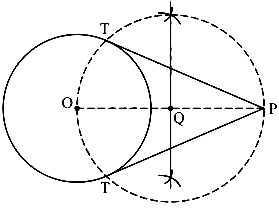
Step of construction
Step I - First of all, we draw a circle of radius AB = 4 cm.
Step II - Mark a point P from the centre at a distance of 6 cm from the point O.
Step III - Draw a right bisector of OP, intersecting OP at Q.
Step IV - Taking Q as centre and radius OQ = PQ, draw a circle to intersect the given circle at T and T’.
Step V - Join PT and PT’ to obtain the required tangents.
Thus, PT and PT' are the required tangents.
Q.3. Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5
Ans. Steps of construction:
1) Draw a line segment AB = 8 cm.
2) Draw a ray AX making an acute angle ∠BAX=60° with AB.
3) Draw a ray BY parallel to AX by making an acute angle ∠ABY = ∠BAX.
4) Mark four points A1, A2, A3, A4 on AX and five points B1,B2,B3,B4,B5 on BY in such a way that AA1=A1A2=A2A3=A3A4.
5) Join A4B5
6) Let this line intersect AB at a point P.
Thus, P is the point dividing the line segment AB internally in the ratio of 4 : 5.
Q.4. Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also measure its length.
Ans. Following are the steps to draw tangents on the given circle:
Step 1 - Draw a circle of 3 cm radius with centre O on the given plane.
Step 2 - Draw a circle of 5 cm radius, taking O as its centre. Locate a point P on this circle and join OP.
Step 3 - Bisect OP. Let M be the midpoint of PO.
Step 4 - Taking M as its centre and MO as its radius, draw a circle. Let it intersect the given circle at points Q and R.
Step 5 - Join PQ and PR. PQ and PR are the required tangents.
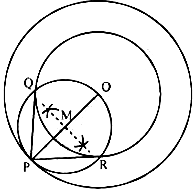
It can be observed that PQ and PR are of length 4 cm each.
In ΔPQO,
Since PQ is a tangent,
∠PQO = 90°
PO = 5 cm
QO = 3 cm
Applying Pythagoras theorem in ΔPQO, we obtain
PQ2 + QO2 = PQ2
PQ2 + (3)2 = (5)2
PQ2 + 9 = 25
PQ2 = 25 − 9
PQ2 = 16
PQ = 4 cm
Hence justified.
Q.5. Draw a circle of radius 3 cm. Form a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents
Ans. Steps of Construction
Step 1: Draw a circle with O as center and radius 3 cm.
Step 2: Mark a point P outside the circle such that OP = 7cm.
Step 3: Join OP. Draw the perpendicular bisector XY of OP. cutting OP at Q.
Step 4: Draw a circle with Q as center and radius PQ (or OQ), to intersect the given circle at the points T and T’.
Step 5: Join PT and PT’.
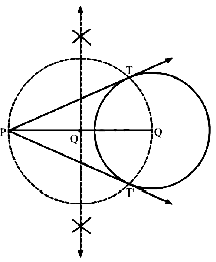
Here, PT and PT’ are the required tangents.
PT = PT ' = 6.3cm(Approx)
Q.6. Draw a circle with radius 4 cm and construct two tangents to a circle such that when those two tangents intersect each other outside the circle they make an angle of 60° with each other
Ans.
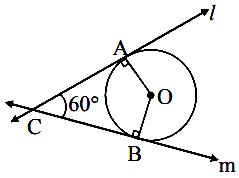
Analysis:
As shown in the figure,
In ▢AOBC,
∠A = ∠B = 90° ......[Tangent theorem]
∠C = 60° ......[Given]
∴ ∠O = 120° ......[Remaning angle of ▢AOBC]
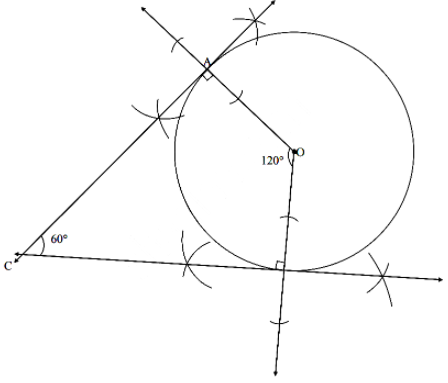
Steps of constructions:
- With centre O, draw a circle of radius 4 cm.
- Take any point A on the circle and draw ray OA.
- Draw line l ⊥ ray OA at point A.
- Draw ray OB such that ∠AOB = 120°. Point B must be on the circle.
- Draw line m ⊥ ray OB at point B.
l and m are the required tangents.
Q.7. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60 .
Ans. 1) Draw a circle of radius 5 cm.
2) Draw horizontal radius OQ.
3) Draw angle 120o from point O. Let the ray of angle intersect the circle at point R.
4) Now draw 90o from point Q.
5) Draw 90o from point R.
6) Where the two arcs intersect, mark it as point P.
Therefore, PQ and PR are the tangents at an angle of 60o.
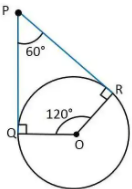
Q.8. Draw a circle of radius 3.5 cm. Draw two tangents to the circle which are perpendicular to each other.
Ans. Steps of construction
Step I. Draw a circle of any convenient radius with O as centre.
Step II. Take a point A on the circumference of the circle and join OA. Draw a perpendicular to OA at point A.
Step III. Draw a radius OB, making an angle of 90° with OA.
Step IV. Draw a perpendicular to OB at point B Let both the perpendicular intersect at point P
Step V. Join OP
PA and PB are the required tangents, which make an angle of 45° with OP.
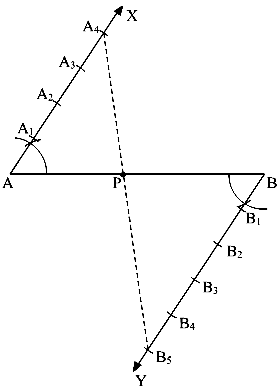
Q.9. Draw a line segment AB = 6 cm and divide it in the ratio of 2 : 3.
Ans. Step I.
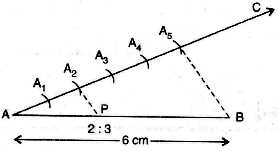
Step II. Steps of construction :
(i) Draw a line segment AB = 6 cm.
(ii) At A draw an acute angle BAC.
(iii) Mark A1,A2,A3,A4,A5, at equal distance.
(iv) Join A5 to B.
(v) Draw a line A2P parallel to A5B.
(vi) P is the required point on AB which divides it in the ratio 2 : 3
Q.10. Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that AP/AB = 3/5.
Ans.
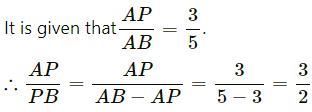
Thus, point P divides line segment AB in the ratio 3: 2.
To draw a line segment AB of length 7 cm and mark a point P (using ruler and compass) such that AP/PB = 3/5i,e, AP/PB = 3/2, the following steps are to be followed:
Step 1: Draw line segment AB of length 7 cm and draw a ray AX making an acute angle with line segment AB.
Step 2: Locate 5 (2 + 3) points i.e., A1, A2, A3, A4 and A5 on AX such that AA1 = A1 A2 = A2 A3 and so on.
Step 3: Join BA5.
Step 4: Through point A3 , draw a line parallel to BA5 (by making an angle equal to ∠AA5 B) at A3 intersecting AB at point P.
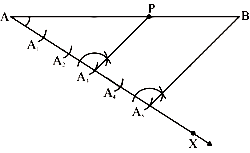
Now, P is the required point on line segment AB of length 7 cm. This point satisfies the condition AP/AB = 3/5.
Chapter
Some Applications Of Trigonometry
Q.1. Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that AP/AB = 3/5.
Ans. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower
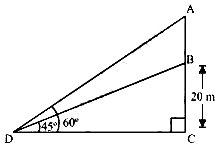
Let BC be the building, AB be the transmission tower, and D be the point on the ground from where the elevation angles are to be measured.
In ΔBCD,
BC/CD = tan 45º
20/CD = 1
CD =20 m
In ΔACD,
AC/CD = tan 60º

Q.2. Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
Ans. Let d be the distance between the two ships. Suppose the distance of one of the ships from the light house is x metres, then the distance of the other ship from the light house is (d−x) metres.
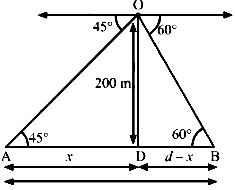
In right-angled ∆ ADO, we have:
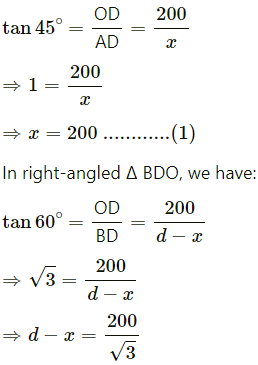
Putting x= 200, we have:
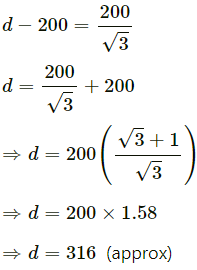
Thus, the distance between two ships is approximately 316 m
Q.3. From the top of a lighthouse 300 m high, the angle of depression of two ships, which are due south of the observer, are 60 degrees and 30 degrees. How can I find their distance apart?
Ans. Let a lighthouse AB = 300m. high , from the top of lighthouse the angle of
depression of two ships C and D are 60° and 30°which are due south of the
observer. Thus angle ACB =60°. and angle ADB. = 30°.
In right ∆ ABC
AB/BC= tan60°
300m/BC= √3. =>. BC= 300/√3m= 100√3 m.
In right ∆ ABD
AB/BD=tan30°
300 m/BD. = 1/√3. =>. BD = 300√3 m.
Distance between two ships = CD = BD - BC
= 300√3- 100√3 =200√3 m. or. 200×1.732. = 346.40 m. Answer.
Q.4. A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45 °. Find the height of the pedestal.
Ans.
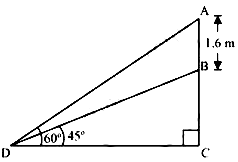
Let AB be the statue, BC be the pedestal, and D be the point on the ground from where the elevation angles are to be measured.
In ΔBCD,
(BC)/(CD) = tan 45º
BC/CB =1
BC= CD
In ΔACD,
(AB+BC)/CD = tan 60º

Q.5. A peacock is sitting on the top of a tree. It observes a serpent on the ground making an angle of depression of 30o. The peacock with the speed of 300 m/min catches the serpent in 12 seconds. What height of the tree?
Ans.

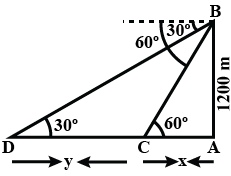
Q.6. An aeroplane at an altitude of 1200 meters finds that two ships are sailing towards it in the same direction . The angle of depression of the ships as observed from the planner are 60∘ and 30∘ respectively. Find the distance between the two ships.
Ans. Let the aeroplane be at B and let the two ships be at C and D such that their angles of depression from B are 60∘ and 30∘ respectively.
We have AB = 1200 metres. Let AC = x and CD = y.
In ΔCAB , we have.

Q.7. From the top of 7m high building, the angle of elevation of the top of a cable tower is 600 and the angle of depression of its foot is 450. Determine the height of the tower
Ans.
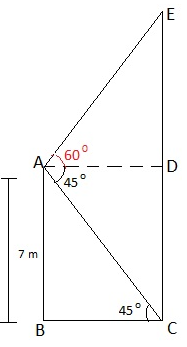
Let us assume that
AB be the building of height 7 m
EC be the height of the tower.
A is the point from where elevation of tower is 60° and the angle of depression of its foot is 45°.
EC = DE + CD
Also, CD = AB = 7 m
BC = AD
From right ΔABC,
tan 45° = AB/BC
1= 7/BC
We get,
BC = 7
Since BC = AD
So AD = 7
Also,
From right triangle ADE,
tan 60° = DE/AD
√3 = DE/7
⇒ DE = 7√3 m
Now:
EC = DE + CD
= (7√3 + 7)
Taking 7 as common, we get,
= 7(√3+1)
Hence,
Height of the tower is 7(√3+1) m.
Q.8. The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
Ans. Let AB be the tower and CD be the hill
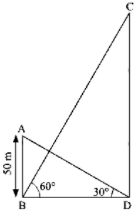
In ΔABD
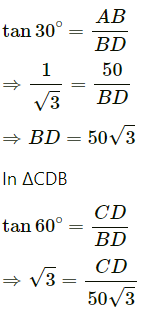
=> CD = 150
Therefore, the height of the hill is 150 m
Chapter
Surface Areas and Volumes
Q.1. 12 solid spheres of same size are made by melting a solid metallic cone of base radius 1 cm and height of 48 cm find the radius of each sphere
Ans. Radius of Each sphere = 1 cm if 12 solid spheres of same size are made by melting a solid metallic cone of base radius 1 cm and height of 48 cm
Step-by-step explanation:
solid metallic cone of base radius 1 cm and height of 48 cm
Volume of Cone = (1/3)πr²h
r = 1 cm
h = 48 cm
Volume of cone = (1/3)π * 1² * 48 cm³
= 16π cm³
Let say radius of sphere = R cm
Volume of Sphere = (4/3))πR³ cm³
Volume of 12 Spheres = 12 * (4/3))πR³ cm³
= 16πR³ cm³
Volume of 12 Spheres = Volume of Cone
=> 16πR³ = 16π
=> R³ = 1
=> R = 1
Radius of Each sphere = 1 cm
Q.2. Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
Ans. Let the edge of each cube be a cm.
Volume of each cube = a3 cm3
It is given that the volume of each cube is 27 cm3.
∴ a3 = 27= (3)3
⇒ a = 3
Thus, length of each edge of the cube = 3 cm
When two cubes are joined end-to-end, the solid obtained is a cuboid whose length, breadth and height are 6 cm, 3 cm and 3 cm respectively.
This can be diagrammatically shown as follows:
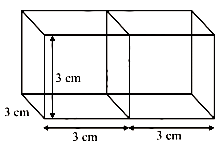
Surface area of the cuboid = 2 (lb + bh + hl)
= 2 (6 cm × 3 cm + 3 cm × 3 cm + 3 cm × 6 cm)
= 2 × 45 cm2
= 90 cm2
Thus, the surface area of the resulting cuboid is 90 cm2.
Q.3. Find the number of plates 1.5 cm in diameter and 0.2 cm thick, that can be fitted completely inside a right circular cylinder of height 10 cm and diameter 4.5 cm.
Ans. Each one of the circular plate is also a cylinder.
Its volume is,

Q.4. A cylindrical glass tube with radius 10 cm has water up to a height of 9 cm, A metal cube of 8 cm edge is immersed completely, By how much the water level will rise in the glass tube ?
Ans. Let the height o water raised measured = h cm
∴ Volume of water displaced in cylinder
Q.5. A solid metallic object is shaped like a double cone. Radius of both cones is same but their heights are different. If this cone is immersed in water, find the quantity of water it wil displace.
Ans.

Q.6. If areas of three adjacent faces of cuboid be x,y and z respectively, then find the volume of the cuboid.
Ans. Let l,b,h be length, breadth & height of the cuboid.
ATQ,
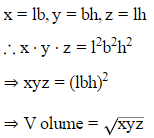
Q.7. Find the volume of the largest right circular cone that can be cut out from a cube of edge 4.2cm.
Ans. Given edge of cube = 4.2cm.
The diameter of the largest circular cone that can be of cone =4.2cm.
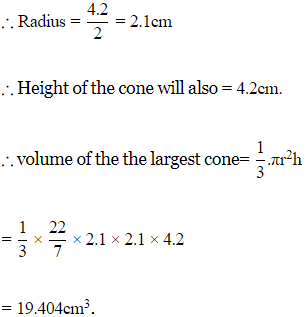
Q.8. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article [Use π = 22/7]
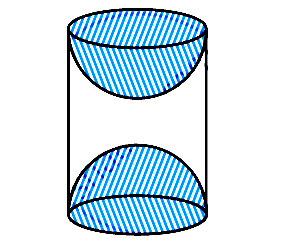
Ans. Given that,
Radius (r) of cylindrical part = Radius (r) of hemispherical part = 3.5 cm
Height of cylindrical part (h) = 10 cm
Surface area of article = CSA of cylindrical part + 2 × CSA of hemispherical part
=2πrh + 2 x ππr2
2π x 3.5 x 1+ + 2 x 2π x 3.5 x 3.5
= 70π+ 49π
= 119π
= 17 x 22 = 374 cm2
Q.9. A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much is canvas cloth required to just cover the heap?
Ans.

Q.10. A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5cm and 13cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Find the surface area of the toy if the total height of the toy is 30cm.
Ans. Height of the cylindrical part = 13cm
Radius of cone , cylinder and hemi sphere = 5cm
r = 5cm for hemisphere cylinder and cone.
Height of cone h = 30 − 5 − 13 = 12
The area of canvas required=Surface area of hemishphere,cylinder and cone parts of tent
Chapter
Statistics
Q.1. Consider the following distribution of daily wages of 50 workers of a factory.
| Daily wages (in Rs.) | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Find the mean daily wages of the workers of the factory by using an appropriate method.
Ans. Find the midpoint of the given interval using the formula.
Midpoint (xi) = (upper limit + lower limit)/2
In this case, the value of mid-point (xi) is very large, so let us assume the mean value, A = 150 and class interval is h = 20.
So, ui = (xi – A)/h = ui = (xi – 150)/20
Substitute and find the values as follows:
| Daily wages (Class interval) |
Number of workers frequency (fi) |
Mid-point (xi) | ui = (xi – 150)/20 | fiui |
| 100-120 | 12 | 110 | -2 | -24 |
| 120-140 | 14 | 130 | -1 | -14 |
| 140-160 | 8 | 150 | 0 | 0 |
| 160-180 | 6 | 170 | 1 | 6 |
| 180-200 | 10 | 190 | 2 | 20 |
| Total | Sum fi = 50 | Sum fiui = -12 |
So, the formula to find out the mean is:
Mean = x̄ = A + h (∑fiui /∑fi) =150 + (20 × -12/50) = 150 – 4.8 = 145.20
Therefore, mean daily wage of the workers = Rs. 145.20
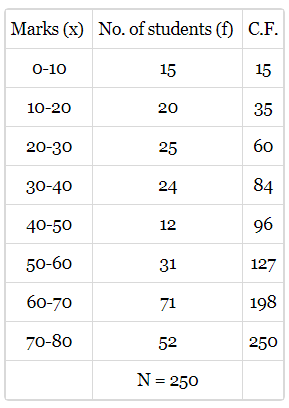
Q.2. Calculate the median from the following data:
| Marks below: | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| No. of students | 15 | 35 | 60 | 84 | 96 | 127 | 198 | 250 |
Ans.

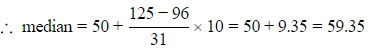
Q.3. The median of the following data is 525. Find the missing frequency, if it is given that there are 100 observations in the data:
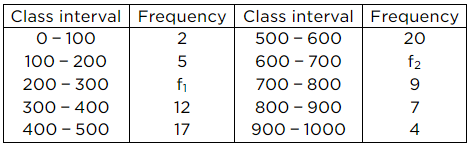
Ans.
| Class interval | Frequency | Cumulative frequency |
| 0 – 100 | 2 | 2 |
| 100 – 200 | 5 | 7 |
| 200 – 300 | f1 | 7 + f1 |
| 300 – 400 | 12 | 19 + f1 |
| 400 – 500 | 17 | 36 + f1 (F) |
| 500 – 600 | 20 (f) | 56 + f1 |
| 600 – 700 | f2 | 56 + f1 + f2 |
| 700 – 800 | 9 | 65 + f1 + f2 |
| 800 – 900 | 7 | 72 + f1 + f2 |
| 900 – 1000 | 4 | 76 + f1 + f2 |
| N = 100 |
Given
Median = 525
Then, median class = 500 – 600
L = 500, f = 20, F = 36 + f1, h = 600 – 500 = 100
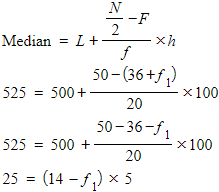
5 = 14 – f1
f1 = 14 – 5 = 9
Given
Sum of frequencies = 100
2 + 5 + f1 + 12 + 17 + 20 + f2 + 9 + 7 + 4 = 100
2 + 5 + 9 + 12 + 17 + 20 + f2 + 9 + 7 + 4 = 100
85 + f2 = 100
f2 = 100 – 85 = 15
f1 = 9 and f2 = 15
Q.4. The following data gives the information on the observed lifetimes (in hours) of 225 electrical components:
| Lifetimes (in hours): | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 | 100-120 |
| No. of components: | 10 | 35 | 52 | 61 | 38 | 29 |
Determine the modal lifetimes of the components.
Ans. From the data given as above its observed that maximum class frequency is 61 which belongs to class interval 60 – 80.
So, modal class limit (l) of modal class = 60
Frequency (f) of modal class = 61
Frequency (f1) of class preceding the modal class = 52
Frequency (f2) of class succeeding the modal class = 38
Class size (h) = 20
Using the formula for find mode, we have
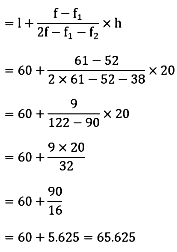
Q.5. The mode of the following data is 67. Find the missing frequency x.
|
Class |
40-50 |
50-60 |
60-70 |
70-80 |
80-90 |
|
Frequency |
5 |
x |
15 |
12 |
7 |
Ans. Given that mode = 67
Modal class=60-70
Mode = l + (f1 – f0)h/(2f1 – f0 – f2)
Here l = lower limit of modal class=60.
h = size of class interval = 10
f1 = frequency of modal class=15
f0 = frequency of class preceding modal class=x
f1 = frequency of class succeeding modal class=12
67 = 60 + (15-x)10/(18-x)
7 = (15-x)10/(18-x)
7(18-x) = 10(15-x)
126 – 7x = 150 – 10x
3x = 24
So x = 24/3
= 8
Hence the value of x is 8.
Q.6. The mean of the following distribution is 48 and sum of all the frequencies is 50. Find the missing frequencies x and y.
| Class | 20 -30 | 30-40 | 40-50 | 50-60 | 60 -70 |
| Frequency | 8 | 6 | x | 11 | y |
Ans.

Q.7. Using an appropriate method, find the mean of the following frequency distribution:
| Class | 84 - 90 | 90 – 96 | 96 – 102 | 102 – 108 | 108 – 114 | 114 – 120 |
| Frequency | 8 | 10 | 16 | 23 | 12 | 11 |
Which method did you use, and why?
Ans.
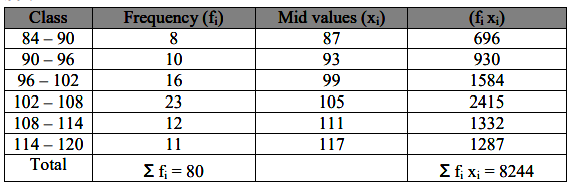
The mean of the data is given by,
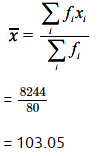
Thus, the mean of the following data is 103.05.







 Profile
Profile Signout
Signout
















 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










