CBSE Class 10 Maths 2024-25: Chapter 10 Circles Competency-Based Questions with Answers; Download Free PDF

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
As the CBSE Class 10 board exams get closer, it’s important for students to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.
This article explores Chapter 10 Circles. It highlights key competency-based questions and provides answers to help students succeed.
Understanding Competency-Based Questions in Chapter 10 Circles
Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.
Competency-based questions in Chapter 10: Circles go beyond memorization, encouraging critical thinking and problem-solving. These questions help students grasp concepts deeply by applying them to real-world scenarios.
CBSE Class 10 Maths Chapter 10: Circles Important Competency-Based Questions
Multiple Choice Questions:-
Q1. In the figure below, ΔPQR is an isosceles triangle with PQ = PR, and the lengths of PU and UR are 5 units and 3 units respectively.
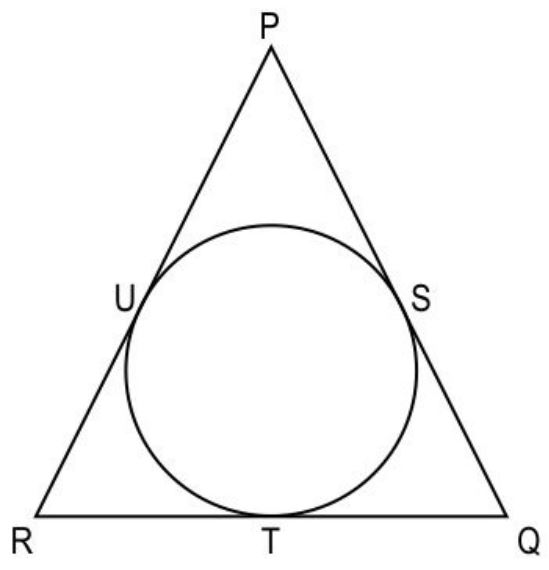
(Note: The figure is not to scale.)
Which of the following is TRUE?
1. PS = 3 units
2. SQ = 5 units
3. QT = 3 units
4. QR = 8 units
Ans. 3. QT = 3 units
Q2. In the figure below, ΔABC is formed using three tangents to a circle centred at O.
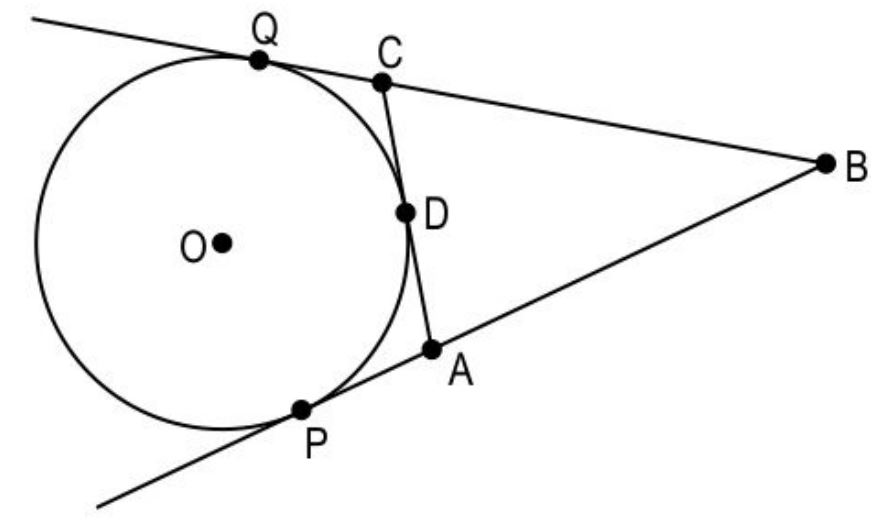
(Note: The figure is not to scale.)
Based on the construction, which of the following statements is true?
1. The sum of the length of BP and BQ less than the perimeter of ΔABC.
2. The sum of the length of BP and BQ is same as the perimeter of ΔABC.
3. The sum of the length of BP and BQ is greater than the perimeter of ΔABC.
4. Length of the tangents should be known to compare it to the perimeter of ΔABC.
Ans. 2. The sum of the length of BP and BQ is same as the perimeter of ΔABC.
Q3. Four tangents of a circle are extended from both the sides to intersect each other until a quadrilateral is formed.
Which of these quadrilateral is NOT possible to be formed?
1. Square
2. Rhombus
3. Rectangle
4. Trapezium
Ans. 3. Rectangle
| Download PDF | |
| CBSE Class 10 Maths Chapter 1 Real Number: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 2 Polynomials: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variable: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 4 Quadratic Equations: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 5 Arithmetic Progressions: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 6 Triangles: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 7 Coordinate Geometry: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 9 Some Applications of Trigonometry: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 10 Circles : Important Competency-Based Questions | Click Here |
Q4. A circle with center O is shown below, where CA and CB are tangents to the circle.
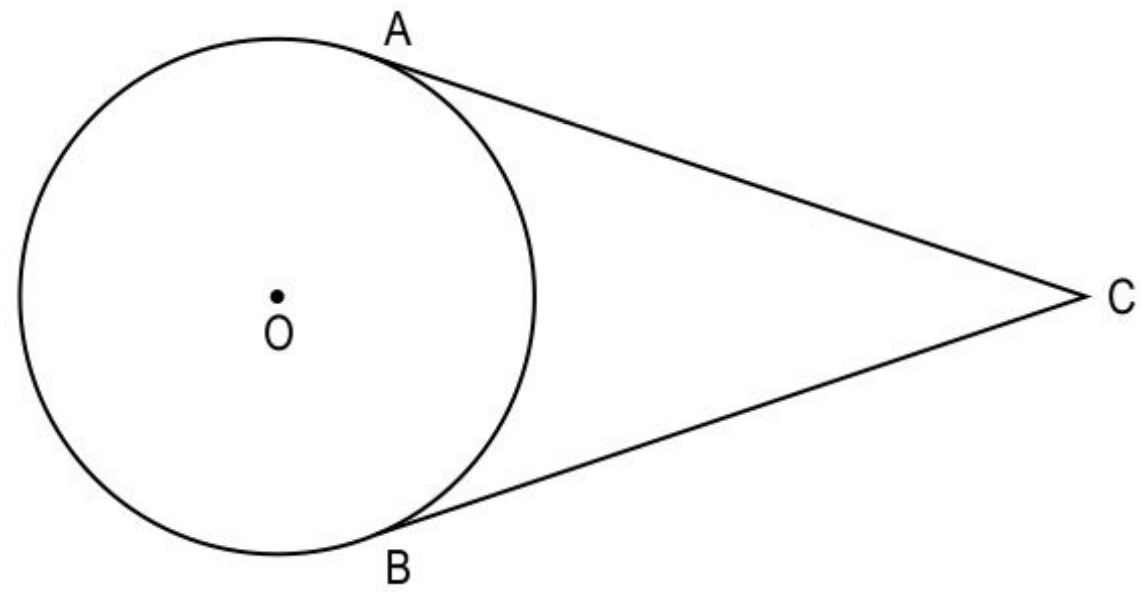
(Note: The figure is not to scale.)
If measure of ∠ACB = 50°, find the measure of ∠AOB.
1. 40°
2. 50°
3. 130°
4. 140°
Ans. 1. 40°
Q5. In the following figure, O is the center of the circle. PQ, QR and RP are tangents of the circle. TS is parallel to QR.
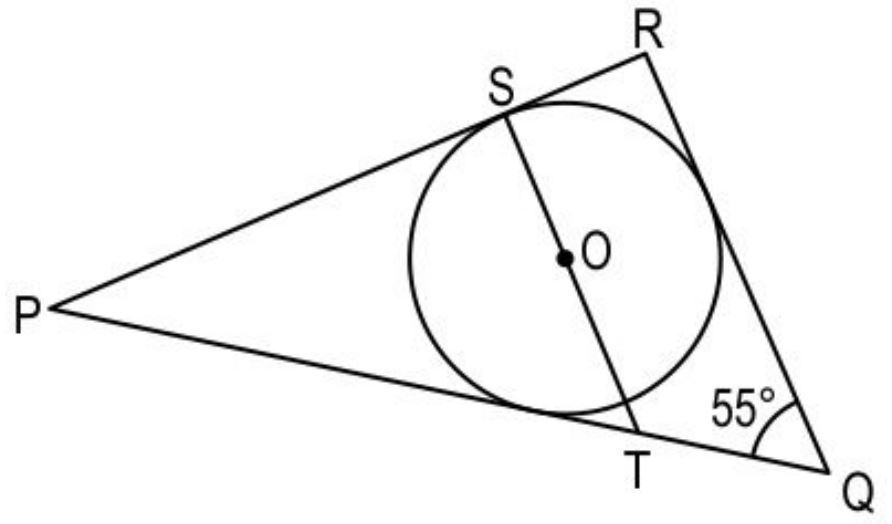
(Note: The figure is not to scale.)
Which of these is the measure of ∠RPQ?
1. 35°
2. 55°
3. 62.5°
4. 70°
Ans. 2. 55°
Q6. How many tangents can be drawn from an external point to a circle?
1. Only 1
2. Only 2
3. Only 3
4. Infinitely many
Ans. 2. Only 2
Assertion & Reason Type Questions :-
Q7. Two statements are given below - one labelled Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
Assertion (A): All angles formed by a chord on the same side of the circumference of a circle are equal to each other.
Reason (R): The sum of any two angles formed by a chord on the opposite sides of the circumference of a circle is 180°.
1. Both (A) and (R) are true and (R) is the correct explanation for (A).
2. Both (A) and (R) are true and (R) is not the correct explanation for (A).
3. (A) is false but (R) is true.
4. Both (A) and (R) are false.
Ans. 2. Both (A) and (R) are true and (R) is not the correct explanation for (A).
Q8. Two statements are given below - one labelled Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
Assertion (A): At the point of contact, a tangent to a circle is always perpendicular to the radius.
Reason (R): The point where a tangent touches a circle is the only point of contact between the tangent and the circle.
1. Both (A) and (R) are true and (R) is the correct explanation for (A).
2. Both (A) and (R) are true and (R) is not the correct explanation for (A).
3. (A) is false but (R) is true.
4. (A) is true but (R) is false.
Ans. 4. (A) is true but (R) is false.
Free Response Questions :-
Q9. AC is a chord to a circle, the length of which is double the radius of the circle.
If B is a point on the circumference of the circle, what is the measure of ∠ABC? Give reason.
Ans. Writes that the measure of ∠ABC is 90°.
States that AC is the diameter of the circle and the angle subtended by diameter on the circumference of the circle is 90°.
Q10. (i) Construct two tangents to a circle of your choice from an external point. Draw the radii at the points of tangency of both the tangents to form a quadrilateral.
(ii) Prove that the line segment joining the external point and the center of the circle divides the quadrilateral into two triangles with equal area.
Show your work.
Ans. (i) Draws a circle with centre O and two tangents AB and AC. Joins OA, OB and OC. The figure may look as follows:
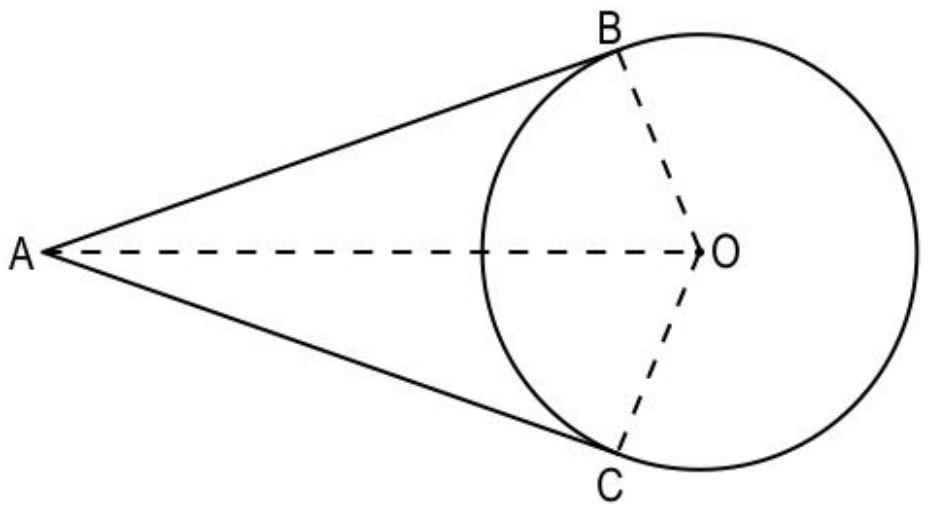
(ii) Writes that, in ΔOAB and ΔOAC, OA is common,
OB = OC (radii of the same circle)
∠OBA = ∠OCA = 90°
Concludes that, ΔOAB is congruent to ΔOAC by RHS congruence criteria. Hence, writes that line segment AO joining the external point and the center of the circle, divides the quadrilateral made by both the tangents and the radius of the circle into two equal parts.
(Award full marks if any other correct method is used. For example, this can also be proved by showing that the heights of two triangles are the same.)
Q11. Given below is a circle with centre O. AB and BC are tangents to the circle from an external point B such that ∠OBA = 35°. D is a point on the circle such that it is NOT on the same line as OB.
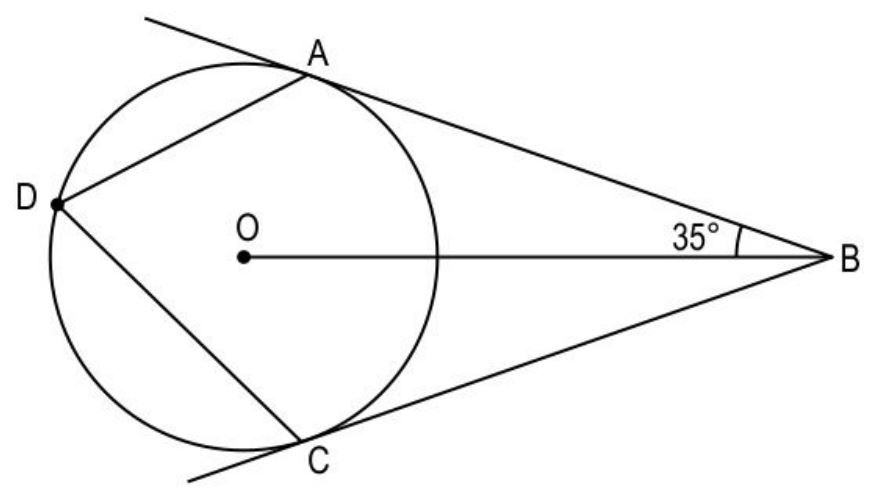
(Note: The figure is not to scale.)
Find the measure of ∠ADC. Show your work.
Ans. Joins OA and OC as follows:
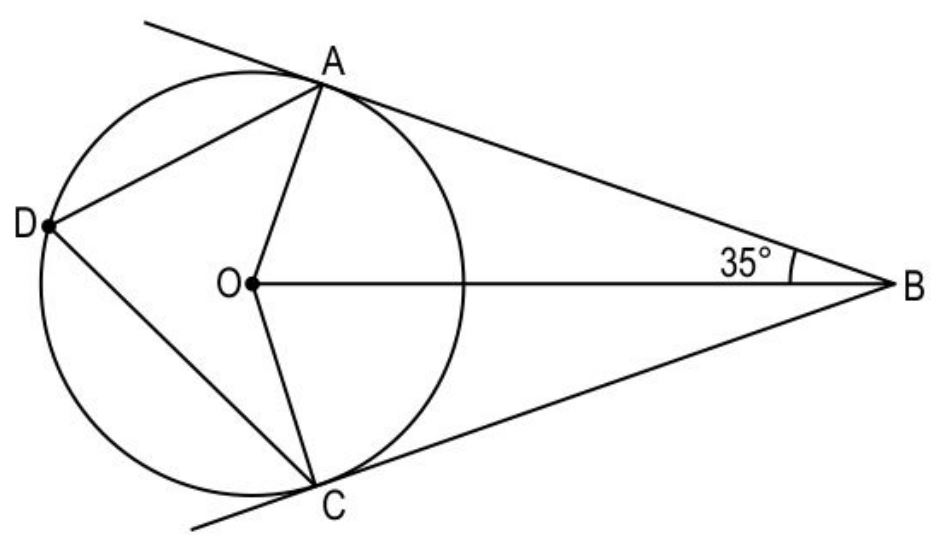
Mentions that in ΔOBA and ΔOBC:
(i) OA = OC (radii of the circle)
(ii) AB = CB (tangents from an external point)
(iii) ∠OAB = ∠OCB = 90° (AB and BC are tangents)
Case Study Based Type Questions :-
Q12. Answer the questions based on the given information.
The game of carrom is played on a square board with a pocket in each corner. They are played using small disks of wood or plastic known as carrom coins. A larger and heavier disk called a striker is used to push these coins across the board to the pockets. The positions of striker and a few coins at different instances in a game are shown in the figure:
P, R and S denote different positions of the striker.
Q, T and U denote different positions of the coins.
O is the centre of the carrom board.
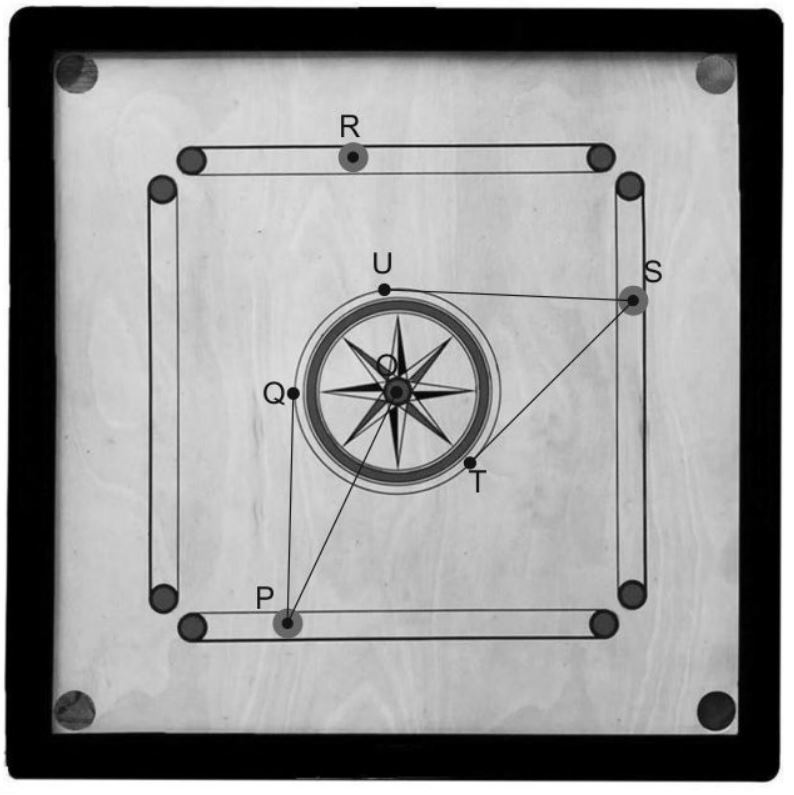
The points P, Q and R do not lie on a straight line. The line PQ touches the circular part of the carrom board only at Q.
(i) The striker at P is 18 cm from the centre and ∠OPQ = 30°.
Find the distance between the striker at P and the coin at Q. Show your work and give valid reasons.
Ans. Finds that OQ is the radius of the circle and hence OQ is perpendicular to PQ.
Writes that in ΔOPQ:
PQ = OPcos 30° = 18 × √3/2
Simplifies the above expression and finds the distance between the striker at P and the coin at Q as 9√3 cm.
(ii) Can QR be a tangent to the circle at Q? Give a valid reason.
Ans. Writes that only one tangent can be drawn from a point on the circle and since PQ and QR are two different straight lines and PQ is a tangent, QR cannot be a tangent to the circle at Q.
(iii) SU and ST are tangents to the circle at U and T respectively and ∠UQT = 55°.
Find ∠UST. Show your work and give valid reasons.
Ans. Finds ∠UOT as 110° and states that angles subtended by an arc at the centre of the circle is double the angle subtended by that arc anywhere on the circle.
Finds that ∠UST = 180° - 110° = 70° as OU is perpendicular to SU, OT is perpendicular to ST and angle-sum property of a quadrilateral.
👉 Read Also- CBSE Class 10 Half-Yearly/Mid Term 2024-25 : Most Important Questions with Answers; PDF Download (All Subjects)
👉 CBSE Class 10 Study Materials
| CBSE Class 10 Syllabus 2024-25 | NCERT Solutions For Class 10 |
| CBSE Class 10 Previous Year Question Papers | CBSE Class 10 Books |
| CBSE Class 10 Full Study Material | CBSE Class 10 Sample Paper |







 Profile
Profile Signout
Signout












 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










