CBSE Class 10 Maths 2024-25: Chapter 2 Polynomials Important Competency-Based Questions with Answers; Download Free PDF

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
As the CBSE Class 10 board exams get closer, it’s important for students to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.
This article explores Chapter 2 Polynomials. It highlights key competency-based questions and provides answers to help students succeed.
Understanding Competency-Based Questions in Chapter 2: Polynomials
Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.
Competency-based questions in Chapter 2: Polynomials go beyond memorization, encouraging critical thinking and problem-solving. These questions help students grasp concepts deeply by applying them to real-world scenarios.
CBSE Class 10 Maths Chapter 2: Polynomials Important Competency-Based Questions
Multiple Choice Questions :
Q1. p ( x ) is a polynomial given by:
p ( x ) = -2 x + 8 x2 - 1
At which of the following points will the graph of p ( x ) intersect the positive x -axis?
(i) 1/2
(ii) 1/4
1. only (i)
2. only (ii)
3. both (i) and (ii)
4. (none, it never intersects positive x -axis)
Ans. 1. only (i)
Q2. Which of these are the zeros of the polynomial x ( x - 7)?
1. only 0
2. only 7
3. both 0 and 7
4. (the polynomial does not have any zero)
Ans. 3. both 0 and 7
Q3. Which of these are the quotient and the remainder when (2 x3 - 9 x + 3x2 + 12) is divided by ( x - 1)?
1. quotient = (2 x2 - 7 x - 4) and remainder = 8.
2. quotient = (2 x2 + 7 x + 4) and remainder = 16.
3. quotient = (2 x2 + 5 x - 4) and remainder = 8.
4. quotient = (2 x2 + 5 x + 4) and remainder = 16.
Ans. 3. quotient = (2 x2 + 5 x - 4) and remainder = 8.
Q4. Which of these is the coefficient of x2 in the quotient when ( x4 + x3 + x + 1) is divided by ( x - 4)?
1. 0
2. -3
3. 5
4. 1
Ans. 3. 5
Q5. (3 a3 - 2 a2 - 9 a + 17) is divided by ( a - 2). What is the coefficient of a in the quotient?
1. -2
2. 3
3. -9
4. 4
Ans. 4. 4
Q6. P( t ) is a polynomial in t such that,
P( t ) = ( t2 + 5t - 14)( t2 - 7t + 10)( t2 + 2 t - 35)
Which of these is the square root of P( t )?
1. ( t + 2)( t - 5)( t +7)
2. ( t - 2)( t - 5)( t +7)
3. ( t + 2)( t + 5)( t -7)
4. ( t - 2)( t - 5)( t -7)
Ans. 2. ( t - 2)( t - 5)( t +7)
Q7. Which of these are the zeroes of x2 + 7 x + 12?
1. 3 and 4
2. (-3) and (-4)
3. (-3) and 4
4. 3 and (-4)
Ans. 2. (-3) and (-4)
Q8. At which point will the graph of the polynomial p ( x ) = (- x + 6 x2 - 1) intersects the negative x -axis?
1. only -1/3
2. only -1/2
3. both -1/3 and -1/2
4. (none, it never intersects negative x -axis)
Ans. 1. only -1/3
| Download PDF | |
| CBSE Class 10 Maths Chapter 1 Real Number: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 2 Polynomials: Important Competency-Based Questions | Click Here |
Free Response Questions :
Q9. (-2/5) is one of the zeroes of the polynomial 5 x2 + 2 x - 7. (T/F)
Justify your answer.
Ans. Writes False(F).
Justifies the answer. For example, substituting x = -2/5 in the given polynomial does not yield 0, so -2/5 is not a zero.
Q10. Given f ( x ) = x3 + 7 x2 + 3 x - 12
Find the value of f (2). Show your work.
Ans. Finds the value of f (2) as:
(2)3 + 7(2)2 + 3(2) - 12 = 30
Q11. f ( x ) = x2 + 10 x + 21
Find the zeroes of the above polynomial. Show your work.
Ans. Factorizes the given polynomial and finds the roots as (-3) and (-7). The working may 1 look as follows:
f ( x ) = x
2 + 10 x + 21 = x
2 + 3 x + 7 x +21 = 0
=> x ( x + 3) + 7( x + 3) = 0
=> ( x + 7)( x + 3) = 0
=> ( x + 7) = 0 or ( x + 3) = 0
=> x = (-7) or x = (-3)
(Note: Award full marks if the correct roots are obtained by any alternative approach.)
Q12. The graph of a polynomial passes through (6, 0), (0, -2) and (-1, 0).
Write two factors of the polynomial. Justify your answer.
Ans. Writes that P( x ) = 0 at x = 6 or P(6) = 0 and hence ( x - 6) is a factor of the 1 polynomial.
(Award 0.5 marks if only the factor is written.)
Writes that P( x ) = 0 at x = -1 or P(-1) = 0 and hence ( x + 1 ) is a factor of the 1 polynomial.
(Award 0.5 marks if only the factor is written.)
Q13. State whether the following statement is true of false. Justify your answer.
If the graph of a polynomial has EXACTLY 2 zeroes, then the polynomial must be quadratic.
Ans. Writes that the statement is false.
Gives reason that while a quadratic polynomial must have a maximum of 2 zeroes, a graph with exactly 2 zeroes need not be that of a quadratic polynomial.
For example: The graph of a cubic polynomial of the form ( x - a )( x - b )2 will have only two zeroes, a and b.
Q14. A quadratic polynomial f ( x ) has two real zeroes that are equal. Adah drew the graph of f ( x ) as shown below.
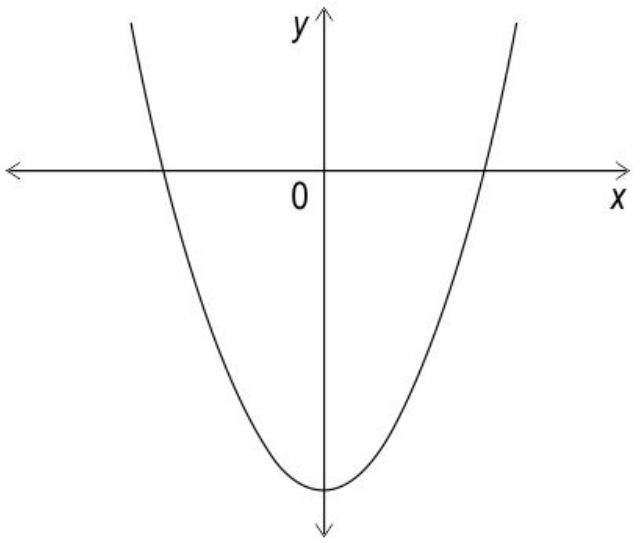
Ans. Writes that the graph Adah has drawn is incorrect.
Gives a valid reason. For example, since f ( x ) has real and equal zeroes, the graph of f ( x ) intersects the x -axis at a unique point.
Q15. Aasira multiplied a variable with 4, subtracted 12 and added the square of the original variable. She expressed the final expression as a product of 2 factors.
Her friend, Rishi, said that the factors will always have a difference of 8.
Is Rishi right? Show your work.
Ans. Assumes the original variable as x and frames the expression as 4 x - 12 + x2.
Factorises the above expression as ( x - 2)( x + 6).
Concludes that Rishi was right as the above factors have a difference of 8.
Q16. When a polynomial is divided by (2 x - 1), the quotient is (3 x - 2) and the remainder is ( x - 3).
Find the polynomial. Show your work.
Ans. Applies the remainder theorem to write the polynomial as:
(2 x - 1)(3 x - 2) + ( x - 3).
Simplifies the above expression to find the polynomial as 6 x2 - 6 x - 1.
Q17. Anand multiplied a variable with 6, subtracted 27 and added the square of the original variable. He expressed the final expression as a product of 2 factors.
His friend, Amit, said that the factors will always have a difference of 6.
Is Amit right? Show your work.
Ans. Assumes the original variable as x and frames the expression as 6 x - 27 + x2.
Factorises the above expression as ( x - 3)( x + 9).
Concludes that Amit was wrong as the above factors have a difference of 12.
Q18. p ( x ) = ( x + 5)2 - 7( x - k ); where k is a constant.
If p ( x ) is divisible by x, find the value of k. Show your steps.
Ans. Simplifies the given polynomial as:
p ( x ) = x2 + 3 x + 7 k + 25
Writes that, if p ( x ) is divisible by x,p (0) = 0.
OR
Writes that the remainder of p(x)/x, which is 7k + 25, should be 0.
Finds the value of k as -25/7.
Case-Based Type Questions :
Q19. Answer the questions based on the given information.
The revenue (in Rs) of a firm is represented by the polynomial R( x ) = 5 x3 + 4 x2 + 7, andthe expenditure (in Rs) by the firm is represented by the polynomial E( x ) = 3 x3 + 2 x - 1 where x is the number of items produced by the firm in a year.
1. Find the profit polynomial P( x ). Show your work.
Ans. Subtracts E( x ) from R( x ) to find P( x ) as 2 x3 + 4 x2 - 2 x + 8.
2. If the firm produces 100 products in a year, find the revenue and profit (in Rs) for the firm using the polynomials. Show your work.
Ans. Finds the revenue made by the company from 100 products as:
R(100) = 5(100)3 + 4(100)2 + 7
=> R(100) = 5000000 + 40000 + 7 = Rs 50,40,007.
Finds the profit made by the company from 100 products as:
P(100) = 2(100)3 + 4(100)2 - 2(100) + 8
=> P(100) = 2000000 + 40000 - 200 + 8 = Rs 20,39,808
3. Tax is calculated on the profit using the polynomial T( y ) = 0.3 y + 100, where y represents the profit earned.
Determine the tax amount (in Rs) to be paid on the profit generated from 10 items.
Show your work.
Ans. Finds profit for 10 items as:
P(10) = 2(10)3 + 4(10)2 - 2(10) + 8
=> P(10) = 2000 + 400 - 20 + 8 = Rs 2388.
Finds tax as:
T(2388) = 0.3(2388) + 100 = Rs 816.4.
Q20. Answer the questions based on the given information.
Shown below is a logo that is made up of two intersecting golden arches, which are parabolic in shape. One such parabola, coinciding with the first arch in the logo, is shown in the graph below.
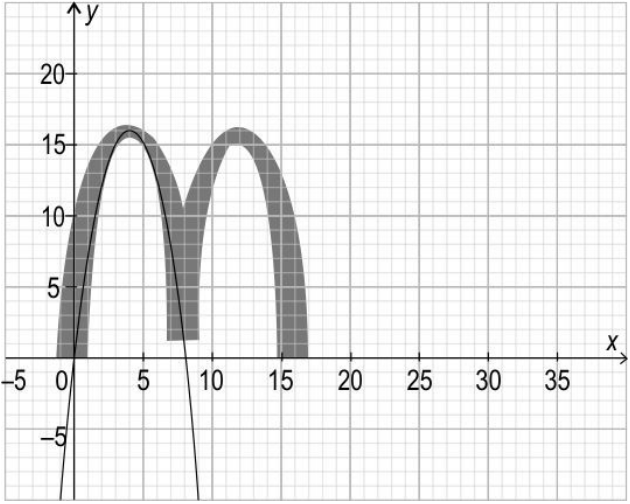
1. Write an equation to represent the parabola shown in the graph.
Show your work and give valid reasons.
Ans. Identifies zeroes of the quadratic equation as 0 and 8.
Identifies that the coefficient of x2 must be negative, since the given parabola is facing downward.
Takes α + β = -b/a = 8 and αβ = c/a = 0, where α and β are the zeroes of the parabola, and a,b and c represent the coefficient of x2, the coefficient of x and the constant respectively.
Finds one equation representing the parabola, by picking a value for a and, 0.5 accordingly choosing values for b and c.
For example, when a = (-1), the required equation is -x2 + 8x = 0.
2. State whether the following statements are true or false.
(i) If the zeroes of the parabola, ax2 + bx + c = 0, coinciding with the second arch in the logo are given by σ and 2σ, then c will be negative.
(ii) If the logo is shifted so that it is symmetrical about the y -axis, then the constant term in the equation of the parabola made by the first arch will be positive.
Justify your answers.
Ans. (i) Writes that the statement is true.
Justifies with a reason. For example,
c/a = 2σ2, which cannot be negative.
a is negative as the parabola is facing downward.
Since a is negative, c must also be negative.
(ii) Writes that the statement is false.
Justifies with a reason. For example,
When the parabola is shifted, the new zeroes of the first arch will be (-8) and 0.
As 0 is a zero of the arch, c = 0. This is because αβ = c/a = 0, where α, β are zeroes of the polynomial.
👉 Read Also- CBSE Class 10 Half-Yearly/Mid Term 2024-25 : Most Important Questions with Answers; PDF Download (All Subjects)
👉 CBSE Class 10 Study Materials
| CBSE Class 10 Syllabus 2024-25 | NCERT Solutions For Class 10 |
| CBSE Class 10 Previous Year Question Papers | CBSE Class 10 Books |
| CBSE Class 10 Full Study Material | CBSE Class 10 Sample Paper |







 Profile
Profile Signout
Signout












 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










