CBSE Class 10 Maths 2024-25: Chapter 6 Triangles Important Competency-Based Questions with Answers; Download Free PDF

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
As the CBSE Class 10 board exams get closer, it’s important for students to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.
This article explores Chapter 6 Triangles. It highlights key competency-based questions and provides answers to help students succeed.
Understanding Competency-Based Questions in Chapter 6: Triangles
Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.
Competency-based questions in Chapter 6: Triangles go beyond memorization, encouraging critical thinking and problem-solving. These questions help students grasp concepts deeply by applying them to real-world scenarios.
CBSE Class 10 Maths Chapter 6: Triangles Important Competency-Based Questions
Multiple Choice Questions
Q. 1 Which of the following may NOT be similar to each other?
i) any two circles
ii) any two rhombuses
iii) any two regular hexagons
1. only ii)
2. only i) and ii)
3. only i) and iii)
4. all - i), ii) and iii)
Answer. (1)
Q.2 Shown below are two triangles ΔMNO and ΔPQR. Dimensions of their two sides are marked in the figure.
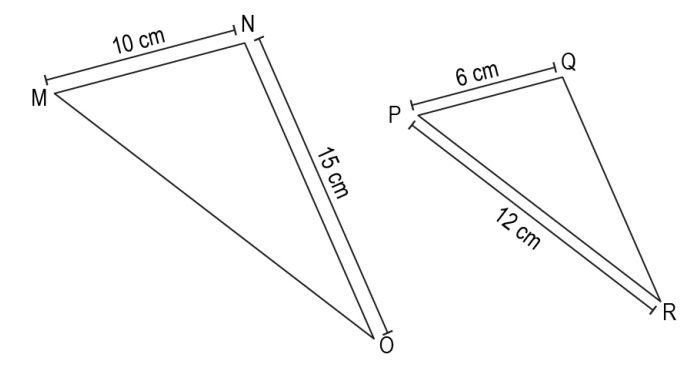
What should be the value of QR if ΔMNO is similar to ΔPQR?
1. 9 cm
2. 11 cm
3. 15 cm
4. 25 cm
Answer. (1)
Q.3 In the following figure, MN is drawn such that M and N are mid-points on JK and KL, respectively.
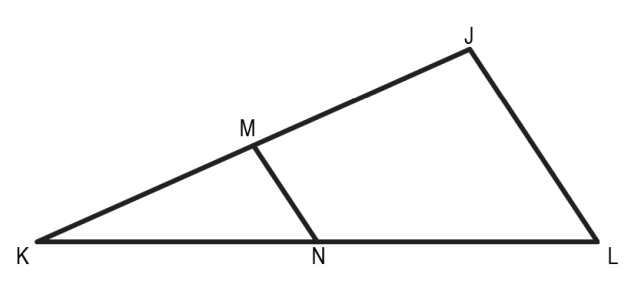
Which of these criteria CANNOT be used to prove that ΔJKL is similar to ΔMKN?
1. SSS similarity criterion
2. SAS similarity criterion
3. AAA similarity criterion
4. (All of the similarity criteria can be used.)
Answer. (4)
Q.4 In the figures given below, ΔSTU and ΔXYZ are similar.
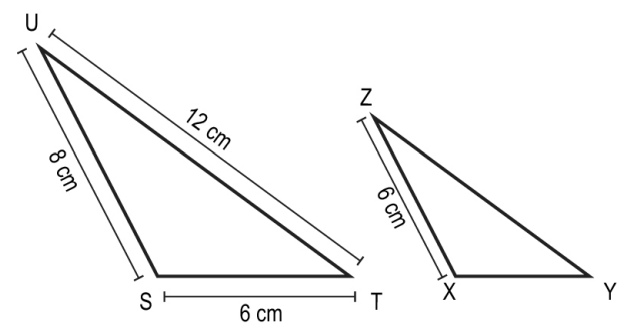
What is the perimeter of ΔXYZ?
1. 19.5 cm
2. 20 cm
3. 26 cm
4. 34.67 cm
Answer. (1)
Q.5 In the ΔXYZ given below, VW || YZ. VY = 6 cm, XY = 14 cm, XW = 12 cm.
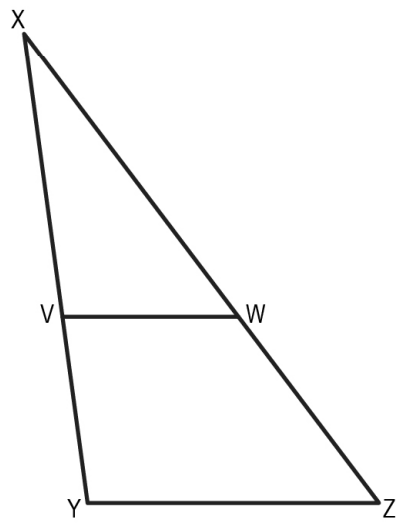
What is the length of XZ?
1.14 cm
2. 21 cm
3. 26 cm
4. 28 cm
Answer. (2)
| Download PDF | |
| CBSE Class 10 Maths Chapter 1 Real Number: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 2 Polynomials: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variable: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 4 Quadratic Equations: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 5 Arithmetic Progressions: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 6 Triangles: Important Competency-Based Questions | Click Here |
Q.6 Danish created an equilateral triangle-shaped rangoli pattern in his room with an area of 10 square units. He replicated the same rangoli pattern in the lobby of his apartment building, where each side of the triangle was 2.5 times the length of the one in his room.
What was the area of rangoli made in the lobby?
1. 25 square units
2. 62.5 square units
3. 156.25 square units
4. (cannot be determined as exact dimensions of the design are required)
Answer. (2)
Q.7 Equal angles have been marked in the triangles below.
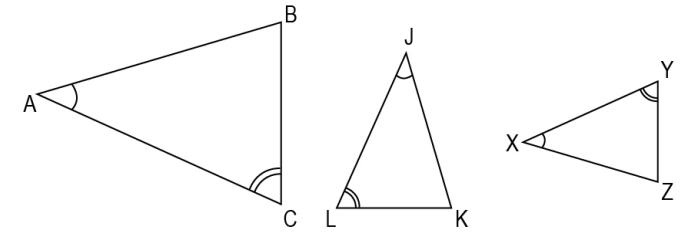
Answer. (2)
Q.8 Which of these is NOT always true?
1. ΔABC ∼ ΔJKL
2. ΔABC ∼ ΔXYZ
3. ΔABC ∼ ΔXZY
4. (All three triangles are similar.)
Answer. (4)
Q.8 The triangles ΔJKL and ΔMNO are similar such that their corresponding sides are in the ratio,

Answer. ()
Q.9 ΔDEF and ΔXYZ are two triangles right angled at point E and Y, respectively. Also,
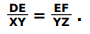
Based on the above information, two statements are given below - one labelled
Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
Assertion(A): ΔDEF is similar to ΔXYZ.
Reason(R): All right angled triangles are similar to each other.
1. Both (A) and (R) are true and (R) is the correct explanation for (A).
2. Both (A) and (R) are true and (R) is not the correct explanation for (A).
3. (A) is false but (R) is true.
4. (A) is true but (R) is false.
Answer. (4)
Free Response Questions
Q.10 Give an example each for when two rectangles are:
i) similar.
ii) not similar.
Answer. i) Writes an example for when two rectangles are similar. For example,
rectangle 1 has length and breadth of 3 cm and 4 cm respectively.
rectangle 2 has length and breadth of 6 cm and 8 cm respectively.
ii) Writes an example for when two rectangles are not similar. For example,
rectangle 1 has length and breadth as 1 cm and 4 cm respectively.
rectangle 2 has length and breadth as 2 cm and 5 cm respectively.
Q.11 A painted cuboid, Solid P, is cut along a plane to get two identical solids. One of the identical solids, Solid Q, is shown below.
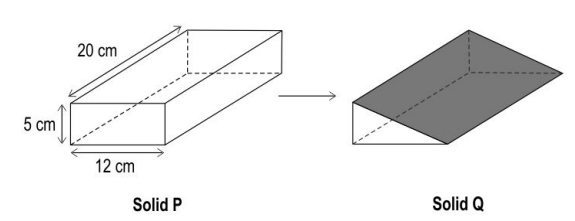
What is the area of the face of Solid Q that is not painted? Show your work.
Answer. Finds the diagonal of the front face of Solid P as √(25 + 144) = 13 cm.
Finds the area of the face of Solid Q that is not painted as 13 × 20 = 260 cm 2 .
Q.12 Shown below is an isosceles right-angled ΔPQR. The area of ΔPQR is 18 cm2 .
Find the length of PR. Show your work.
Answer. Assumes PQ = QR as m and writes the equation for the area of the triangle as:
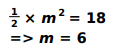
Uses the Pythagoras theorem to find the length of PR as:
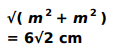
Q.13 Shown below is a figure. ΔPQR is a right-angled triangle. There are 3 semicircles with diameters as sides of ΔPQR. All length measurements are in cm.
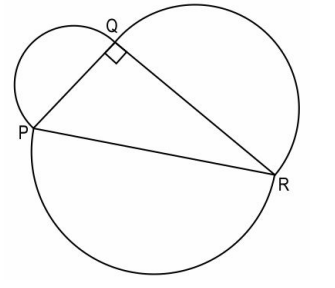
Show that the sum of the areas of semicircles with diameters PQ and QR is equal to the area of semicircle with diameter PR.
Answer. Finds the area of semicircle with diameter PQ as:


Hence, concludes that the sum of the areas of semicircles with diameters PQ and QR is equal to the area of semicircle with diameter PR.
Q.14 Shown below is a figure with two rectangles. The ratio of UV:VW = QR:RS = 3:4. Area of TUVW is 36 cm2 .
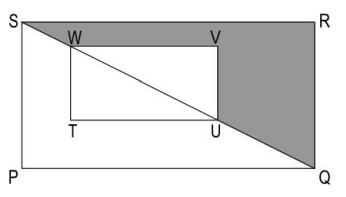
What is the area of the shaded region? Show your work.
Answer. Writes that in ΔUVW and ΔQRS,

Finds the area of the shaded region as 32 - 18 = 14 cm 2
Q.15 i) Two chords of a circle, PQ and MN intersect at a point T. Show that PT × TQ = MT × TN. Draw a figure.
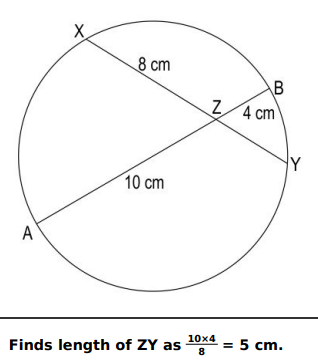
ii) Shown below is a circle with centre O. Use the result from part i) to find the length of ZY. Show your work.
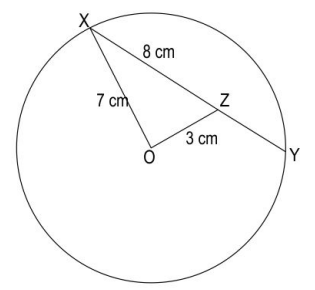
Answer. i) Draws a circle with chords PQ and MN. Joins PM and QN to form ΔPMT and ΔNQT.The figure may look as follows:
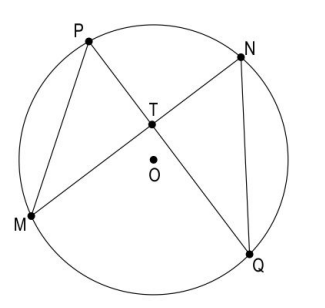
Writes that in ΔPMT and ΔNQT,
∠PMT = ∠NQT (angles in the same segment subtended by the same arc)
∠TPM = ∠TNQ (angles in the same segment subtended by the same arc)
Hence, ΔPMT ∼ ΔNQT by AA similarity criterion.
Uses the above to write the ratio of sides as:
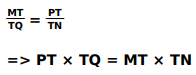
ii) Draws a rough figure with diameter AB. The figure may look as follows:
Q.16 In the figure below, P, Q and R are collinear. P and Q are centres of the two circles. P lies on the circumference of the circle with centre Q. R is 10 cm from Q and 15 cm from P. Both circles have 2 common tangents from point R.
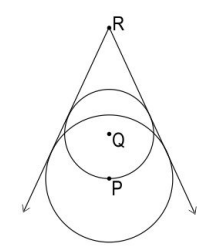
Answer. Draws a rough figure with the radii of the two circles. The figure may look as follows:
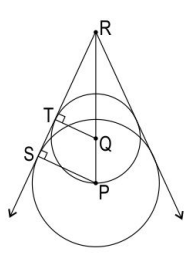
Writes that in ΔPSR and ΔQTR,
∠PRS = ∠QRT (common)
∠PSR = ∠QTR = 90° (radius is perpendicular to the tangent at the point of contact)
Q.17 Anuradha painted the front of the roof of her house, shown by the isosceles right-angled ΔABC in the figure below. The area painted by her is 18 m2 .
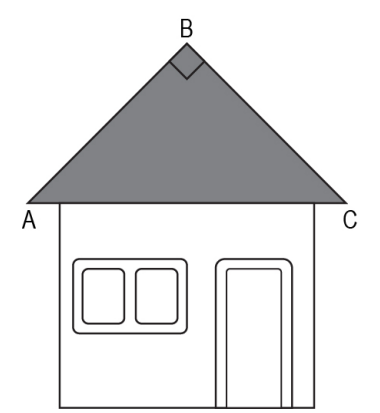
She wants to hang string lights in a straight line along AC, for decoration.
Find the length of string lights Anuradha will need. Show your work.
Answer. Assumes AB = BC as p and writes the equation for the area of the triangle as:
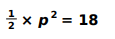
Using the above equation, finds p as 6 m.
Uses the Pythagoras theorem to find the length of string lights required (length of AC) as:
√( p 2 + p 2 )
= √(62 + 62 )
= 6√2 m
Q.18 A graffiti artist wants to create a design on a wall using two triangles. He draws a miniature version of the artwork in his notebook, as shown below.
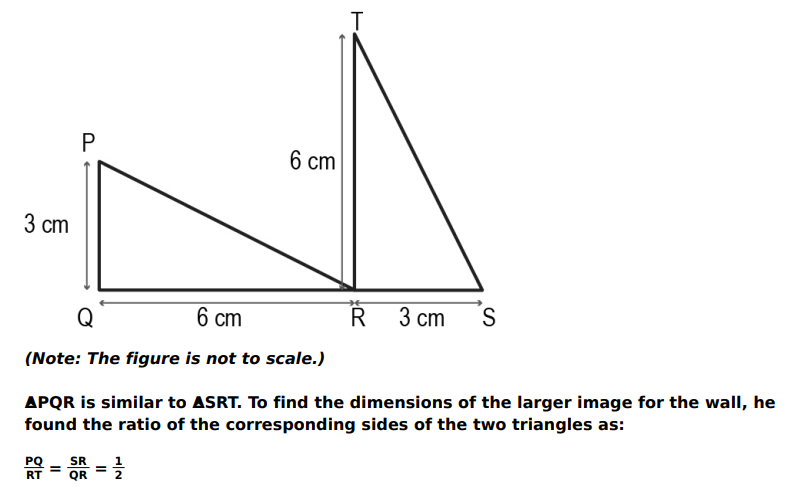
Answer. Writes that the the given ratio of sides is not correct.
Gives a valid reason. For example, the corresponding sides of ΔPQR and ΔSRT are QR and RT respectively. Hence, the ratio of the corresponding sides is 1.
Case Study-based Questions
Answer the questions based on the given information.
The rectangular playing top of a pool table is 220 cm long and 110 cm wide. It has 4 pockets in the corners. When a ball hits a side of the table, it bounces off the side at the same angle as it hit that side. There are two kinds of balls - a white cue ball and 15 numbered coloured balls. The cue ball must be used hit a numbered ball into one of the pockets. Shown below is a pool table.
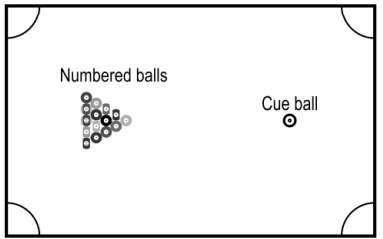
Q.19 Tanmay had hit a numbered ball into pocket P. The path followed by the cue ball and ball 8 is shown below. The cue ball's initial distance from the edges of the table is marked in the figure.
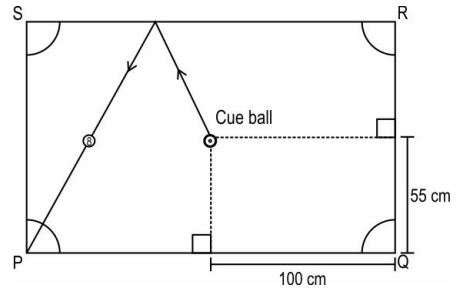
What is the distance of the cue ball from pocket S when the ball hits side RS? Draw a diagram and show your work.
Answer. Assumes SU as x cm and draws a rough diagram. The figure may look as follows:
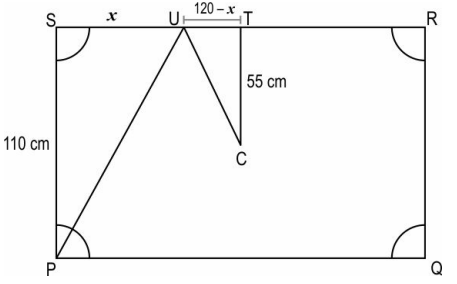
Writes that, in ΔPSU and ΔCTU,
∠PSU = ∠CTU = 90°
∠SUP = ∠CUT (Angle at which ball hits = angle at which it bounces off)
Uses the above step to conclude that by AA criterion of similarity of triangles, ΔPSU 0.5 ∼ ΔCTU.
Writes the ratio of the sides as:
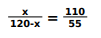
Solves the above equation for x to find the distance of the ball from pocket S when the ball hits side RS as 80 cm.
Q.20 Shown below is the path when Tanmay hits a ball number 1 in pocket S. The distance CT is 50 cm and TS is 120 cm. The cue ball hits the side PQ at an angle of 45°.
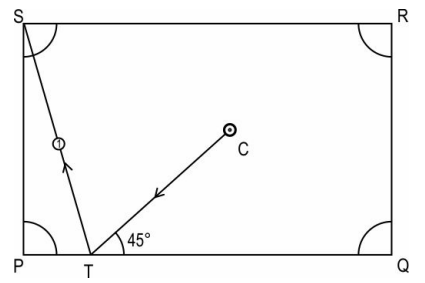
Find the distance between the cue ball's initial position and pocket S. Draw a rough figure, show your work and give valid reasons.
Answer. Draws a rough diagram. The diagram may look as follows:
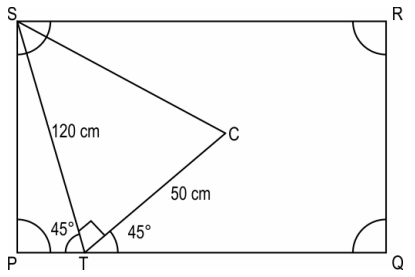
Writes that, since the ball bounces off the side at the same angle as it hit that side, ∠CTS = 90°.
Writes that, by using the Pythagoras theorem in ΔWVU, the distance between the cue ball's initial position and pocket S is √(502 + 1202 ) = 130 cm.
-
👉 Read Also- CBSE Class 10 Half-Yearly/Mid Term 2024-25 : Most Important Questions with Answers; PDF Download (All Subjects)
👉 CBSE Class 10 Study Materials
| CBSE Class 10 Syllabus 2024-25 | NCERT Solutions For Class 10 |
| CBSE Class 10 Previous Year Question Papers | CBSE Class 10 Books |
| CBSE Class 10 Full Study Material | CBSE Class 10 Sample Paper |







 Profile
Profile Signout
Signout












 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










