Haryana Board 10th Exam 2024 : Mathematics Most Important Question with Answers

हरियाणा बोर्ड कक्षा 12 Maths - गणित के लिए महत्वपूर्ण प्रश्न उपलब्ध हैं। हरियाणा बोर्ड 12वीं की  Maths - गणित परीक्षा 11th March, 2024 को निर्धारित है। तो यह आर्टिकल आपके लिए काफी ज्यादा महत्वपूर्ण साबित होने वाला है क्योंकि इस आर्टिकल में आपको बोर्ड परीक्षा के लिए वो ही प्रश्न दिए गए है जो बोर्ड पेपर में आने जा रहे है।

यहाँ पर हरियाणा Board क्लास 12th के Maths - गणित (Haryana Board Maths - गणित Class 12th Exam 2024 VVI Most Important Question) से संबंधित महत्वपूर्ण प्रश्न दिए गए है। महत्वपूर्ण प्रश्नों का एक संग्रह है जो बहुत ही अनुभवी शिक्षकों के द्वारा तैयार किये गए है। इसमें प्रत्येक महत्वपूर्ण प्रश्नों को छांट कर एकत्रित किया गया है, जिससे कि विद्यार्थी कम समय में अच्छे अंक प्राप्त कर सके।

1. यदि 65 और 117 का HCF 65m 117 के रूप में व्यक्त किया जा सकता है, तो m का मान है:
(a) 4
(b) 2
(c) 1
(d) 3

Ans: (b) 2

2. यदि p² = 32/50 है, तो p एक/एक है:
(a) पूर्ण संख्या
(b)पूर्णांक
(c) परिमेय संख्या
(d) अपरिमेय संख्या

Ans: (c) परिमेय संख्या

3. द्विघात समीकरण 2x² – √5x + 1 = 0 के है:
(a) दो भिन्न वास्तविक मूल
(b) दो समान वास्तविक मूल
(c) कोई वास्तविक मूल नहीं
(d) दो से अधिक वास्तविक मूल

Ans: (c) कोई वास्तविक मूल नहीं

4. दो एपी (AP) का सामान्य अंतर समान है। इनमें से एक का पहला पद -2 है और दूसरे का - 6 है। तो उनके 5वें पद के बीच का अंतर है
(a) 2
(b) -2
(c) 4
(d) -4

Ans: (c) 4

5. वह बिंदु जो बिंदु A (-2,-5) और B (2, 5) को जोड़ने वाले रेखा खंड के लंब समद्विभाजक पर स्थित है:
(a) (0,0)
(b) (0,2)
(c) (2,0)
(d) (-2,0)

Ans: (a) (0,0)

6. यदि बिंदु P से केंद्र O वाले वृत्त पर स्पर्श रेखाएँ PA और PB एक दूसरे पर 80° के कोण पर झुकी हों, तो ZPOA बराबर है:
(a) 50°
(b) 60°
(c) 70°
(d) 80°

Ans: (a) 50°

7. दो अंकों की सबसे छोटी भाज्य संख्या और सबसे छोटी भाज्य संख्या का LCM है:
(a) 4
(b) 12
(c) 20
(d) 44

Ans: (c) 20

8. 441 के अभाज्य गुणनखंडन में 7 का घातांक है:
(a) 1
(b) 2
(c) 3
(d) 4

Ans: (b) 2

9. k का वह मान जिसके लिए समीकरण 2x² – kx + k = 0 के मूल समान हैं, है:
(a) 0 केवल
(b) 4
(c) 8 केवल
(d) 0,8

Ans: (d) 0,8

10. यदि किसी वृत्त के व्यास के एक छोर के निर्देशांक (2,3) हैं और केंद्र के निर्देशांक (-2,5) हैं, तो व्यास के दूसरे छोर के निर्देशांक हैं
(a) (-6,7)
(b) (-6,-7)
(c) (6,-7)
(d) (6,7)

Ans: (a) (-6,7)

11. यदि 6 मीटर ऊंचे खंभे की छाया जमीन पर 2√3 मीटर लंबी पड़ती है, तो सूर्य का उन्नतांश है:
(a) 30°
(b) 60°
(c) 15°
(d) 75°

Ans: (b) 60°

12. वह न्यूनतम संख्या जो 1 से 10 तक (दोनों मिलाकर) सभी संख्याओं से विभाज्य हो, है
(a) 10
(b) 100
(c) 504
(d) 2520

Ans: (d) 2520

13. मान लीजिए p एक अभाज्य संख्या है। तो इसके गुणनखंडों का योग है
(a) p
(b) 1
(c) p -1
(d) p+1

Ans: (d) p+1

14. यदि I, m, n A P. में हैं तो 1³ + m³ - 8n³ बराबर है
(a) 4 Imn
(b) -6lmn
(c) 2lmn
(d) 8lmn

Ans: (b) -6lmn

15. X- अक्ष से बिंदु (-1,7) की दूरी है:
(a) √50
(b) 7
(c) 6
(d) -1

Ans: (b) 7

16. यदि एक ही आधार, त्रिज्या r के दो ठोस अर्धगोलार्थों को उनके आधारों के अनुदिश एक साथ जोड़ा जाता है, तो नए ठोस का वक्र पृष्ठीय क्षेत्रफल है:
(a) 4πr²
(b) 4π²r²
(c) 3πr²
(d)8πr²

Ans: (a) 4πr²

17. निम्नलिखित में से कौन सी घटना की प्रायिकता नहीं हो सकती ?
(a) 1/3
(b) 0.1
(c) 3%
(d) 17/16

Ans: (d) 17/16

18. यदि दो धनात्मक पूर्णांक p और q को p = ab² और q = a³ b के रूप में व्यक्त किया जा सकता है;
a, b अभाज्य संख्याएँ हैं, तो LCM (p, q) है:
(a) ab
(b) a²b²
(c)a³b²
(d) a³b³

Ans: (c)a³b²

19. यदि LCM(91, 26) = 182. तब HCF (91, 26) है:
(a) 13
(b) 26
(c) 18
(d) 9

Ans: (a) 13

20. निम्नलिखित में से कौन सी एक अपरिमेय संख्या नहीं है?
(a) √2
(b) √3
(c) √4
(d) √5

Ans: (c) √4

21. यदि a और B, 5 x 2 x +4 के शून्यक हैं, तो ap का मान है:
(a) 1/5
(b) 4/5
(c) 5/4
(d) -4/5

Ans: (b) 4/5

22. निम्नलिखित में से किस समीकरण का मूल 2 है?
(a) x² -4x + 5 = 0
(b) x² + 3x -12 = 0
(c) 2x² -7x + 6 = 0
(d) 3x² - 6x - 2 = 0

Ans: (c) 2x² -7x + 6 = 0

23. उस AP का 18वाँ पद बताओ जिसके पहले दो पद -6 और 1 हैं:
(a) 113
(b) 112
(c) 110
(d) 107

Ans: (a)113

24. बिंदु P(2,3) की मूल बिंदु से दूरी है:
(a)13
(b)√13
(c) √5
(d) √7

Ans: (b)√13

25. यदि sinθ-cosθ = 0, तो θ का मान है:
(a) 30°
(b) 45°
(c) 90°
(d) 0⁰

Ans: (b) 45°

26. k के किस मान (मानों) के लिए समीकरण युग्म kx +3y = k-3 12x + ky =k का कोई हल नहीं है?

Ans: 

27. चित्र में. OA.OB = OC.OD दिखाएँ कि ∠A = ∠C और ∠B = ∠D 

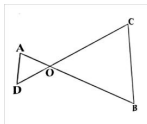
Ans:

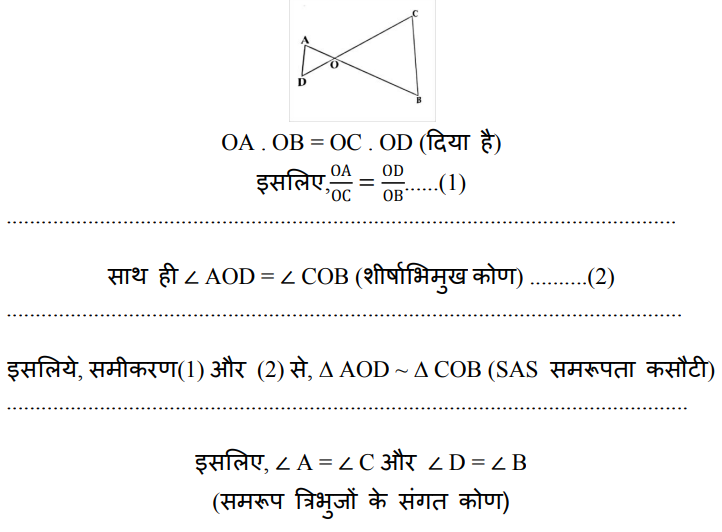
28. दो संकेंद्रीय वृत्तों की त्रिज्याएँ 5 सेमी और 3 सेमी हैं। बड़े वृत्त की उस जीवा की लंबाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती है।

Ans:  

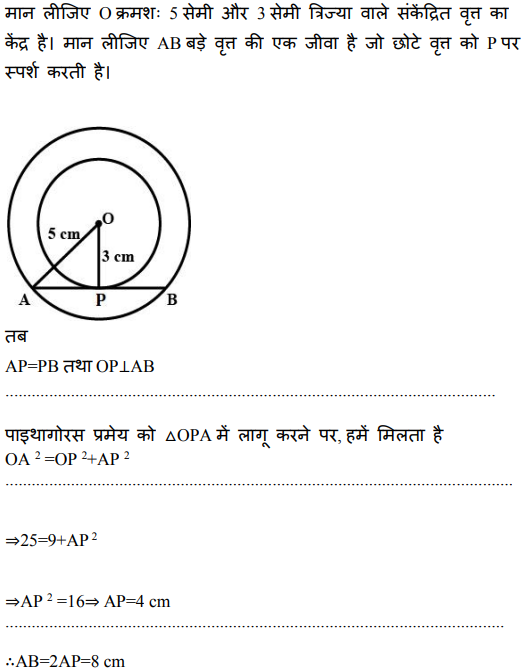
29. 

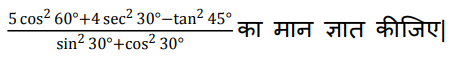
Ans: 

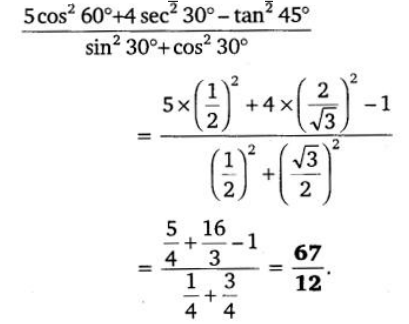
30. सिद्ध कीजिए कि 3-2√5 एक अपरिमेय संख्या है, दिया गया है कि √5 एक अपरिमेय संख्या है। 

Ans:

31. 

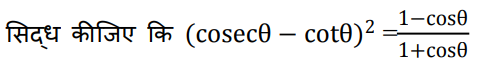
Ans:

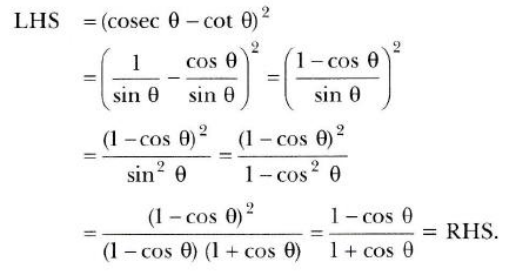
7. k का मान ज्ञात करें जिसके लिए रैखिक समीकरण युग्म 2x + 3y - 5 = 0 और kx -6y -8 = 0 का एक अद्वितीय हल है।

Ans:

32. यदि बिंदु A(6,1),B(8,2),C(9,4) और D(p,3) क्रम में लिए गए समांतर चतुर्भुज के शीर्ष हैं, तो p का मान ज्ञात कीजिए।

Ans: हम जानते हैं कि समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।

इसलिए, विकर्ण AC के मध्य-बिंदु के निर्देशांक विकर्ण BD के मध्य-बिंदु के निर्देशांक के समान हैं।

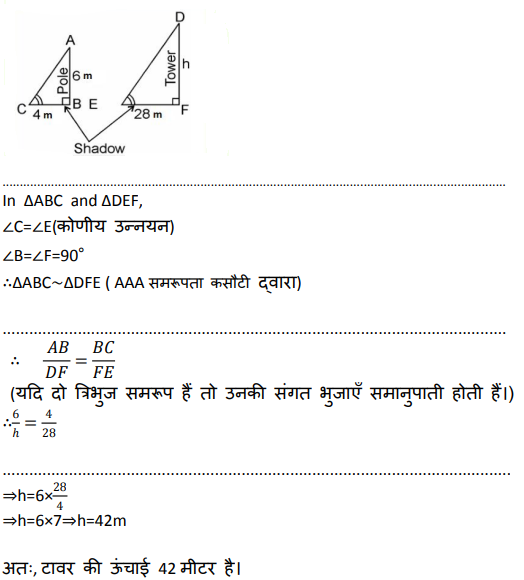
33. 6 मीटर लंबे एक ऊर्ध्वाधर खंभे की छाया जमीन पर 4 मीटर लंबी पड़ती है और उसी समय एक टावर की छाया 28 मीटर लंबी पड़ती है। टावर की ऊँचाई ज्ञात कीजिए।

Ans: 

34. सिद्ध कीजिए कि √2 + √3 अपरिमेय संख्या है।

Ans: 

35. सिद्ध कीजिए की (sin⁴θ – cos⁴θ + 1) cosec²θ = 2.

Ans: 

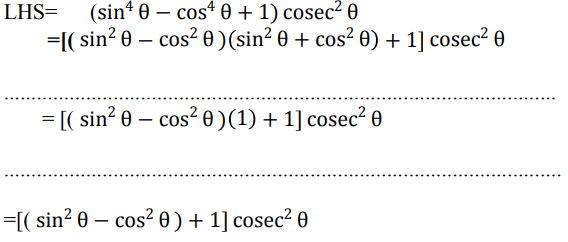
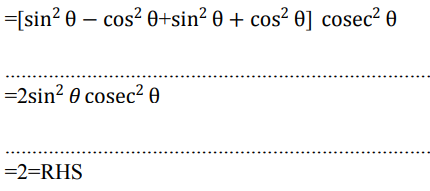
36. 80 मीटर चौड़ी सड़क के दोनों ओर समान ऊंचाई के दो खंभे एक-दूसरे के विपरीत खड़े हैं। सड़क पर उनके बीच एक बिंदु से, खंभों के शीर्ष का उन्नयन कोण क्रमशः 60° और 30° है। खंभों की ऊंचाई और खंभे से बिंदु की दूरी ज्ञात कीजिए।

Ans: 

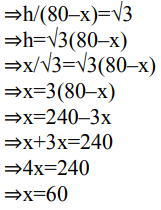
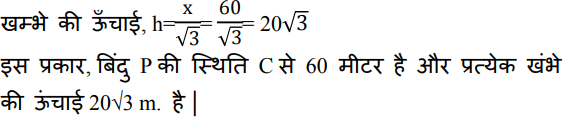
37. 21.यदि समीकरण युग्म 3x-y-5 = 0 और 6x -2y-k= 0 का कोई हल नहीं है, तोk का मान ज्ञात कीजिए |

Ans:

14. त्रिभुज ABC की भुजा BC पर D इस प्रकार एक बिंदु है

Ans: 

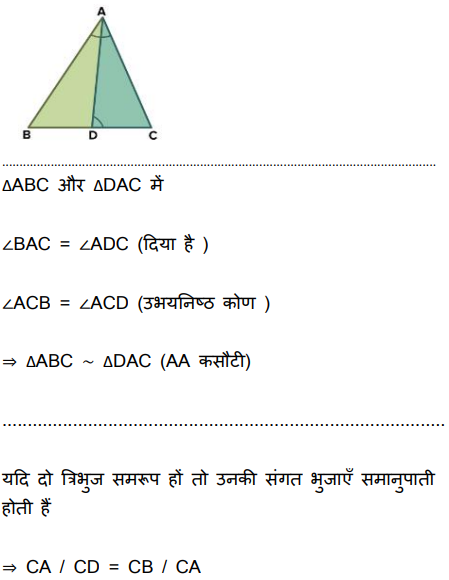
38. 

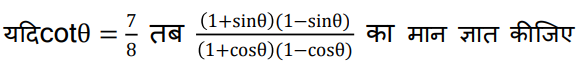
Ans:

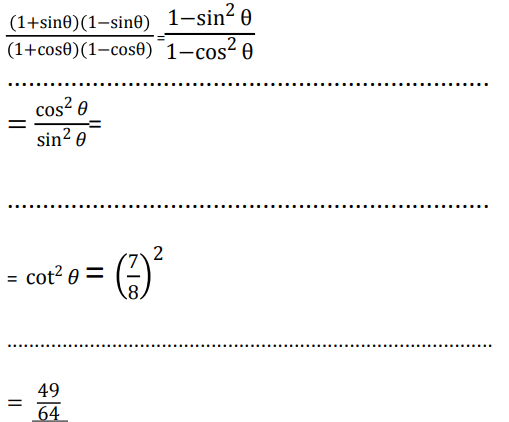
39. सिद्ध कीजिए कि 3 + 2√5 एक अपरिमेय संख्या है।

Ans: 

40. बहुपद x² + 1/6 x -2 के शून्यक ज्ञात करें, और बहुपद के गुणांकों और X शून्यकों के बीच संबंध को सत्यापित करें।

Ans: 

40. एक बॉक्स में 90 डिस्क हैं जिन पर 1 से 90 तक संख्याएं अंकित हैं। यदि बॉक्स से एक डिस्क यादृच्छिक रूप से निकाली जाती है, तो प्रायिकता ज्ञात कीजिए कि उस पर (i) दो अंकों की संख्या (ii) एक पूर्ण वर्ग संख्या (iii) 5 से विभाज्य संख्या अंकित है।

Ans: 

41. एक समकोण त्रिभुज की ऊंचाई उसके आधार से 7 सेमी कम है. यदि कर्ण 13 सेमी है, तो अन्य दो भुजाएँ ज्ञात कीजिए।

Ans: एक समकोण त्रिभुज में ऊँचाई एक भुजा होती है।
माना कि आधार x सेमी है।
ऊँचाई (x - 7) सेमी होगी ।
अब हम पाइथागोरस प्रमेय को दिए गए समकोण त्रिभुज पर
लागू कर सकते हैं।
पाइथागोरस प्रमेय: (कर्ण)² = (भुजा1)² + (भुजा2)²
(13)² = x² + (x - 7)²
169 = x² + x² - 14x + 49
169 = 2x² - 14x + 49
2x² - 14x + 49 -169 = 0
2x² - 14x - 120 = 0
(2x² - 14x-120)/2 = 0
x² - 7x - 60 = 0
x²- 12x + 5x - 60 = 0
x(x - 12) + 5 (x - 12) = 0
(x+5) (x - 12) = 0
x-12 = 0 and x + 5 = 0
x = 12 and x = -5

42. एक ठोस लोहे का खंभा ऊंचाई 220 सेमी और आधार व्यास 24 सेमी का एक सिलेंडर है, जिसके ऊपर ऊंचाई 60 सेमी और त्रिज्या 8 सेमी का एक और सिलेंडर बना है। खंभे का द्रव्यमान ज्ञात करें, जबकि 1 सेमी³ लोहे का द्रव्यमान लगभग 8 ग्राम है। (r= 3.14 उपयोग करें)

Ans: 

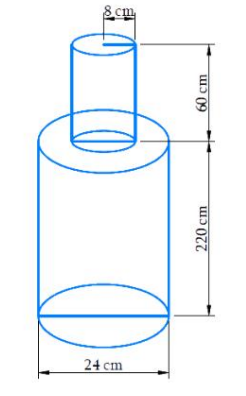
बड़े बेलन की त्रिज्या = 12 सेमी, बड़े बेलन की ऊंचाई = 220 सेमी
छोटे बेलन की त्रिज्या = 8 सेमी, छोटे बेलन की ऊंचाई = 60 सेमी
बड़े बेलन का आयतन = πr²h
=π × 12² x 220
= 31680 πcm³
छोटे बेलन का आयतन = πr²h
= π x 8² x 60
= 3840π cm³
ठोस लोहे के खंभे का आयतन = बड़े बेलन का आयतन + छोटे बेलन का आयतन= 31680π + 3840π = 35520π cm³
खंभे का द्रव्यमान = घनत्व x आयतन = 8x35520 = 8× 35520 × 3.14
= 892262.4gm = 892.3kg

43. बिंदुओं (- 3, 10) और (6, 8) को मिलाने वाले रेखाखंड को बिंदु (- 1,6). जिस अनुपात में विभाजित करता है। वह अनुपात ज्ञात कीजिए।

Ans: 

44. ΔPQR की भुजाओं PR और QR पर S और T इस प्रकार बिंदु हैं कि

Ans: 

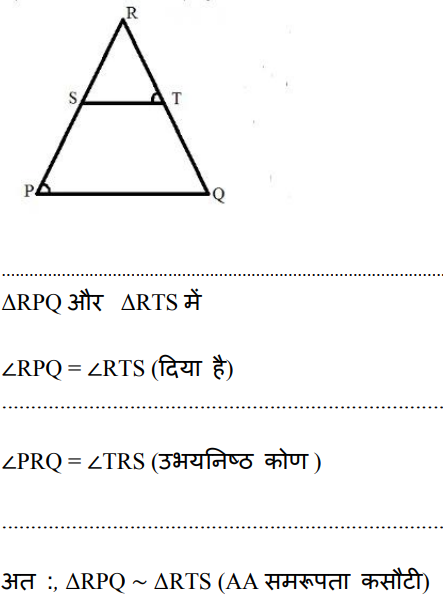
45. 

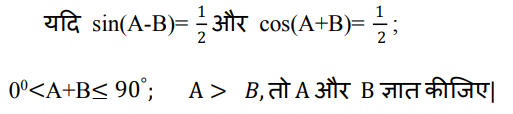
Ans:

46. एक राजमार्ग पर स्थान A और B 100 किमी दूर हैं। एक ही समय में एक कार A से और दूसरी B से प्रारंभ होती है। यदि कारें अलग-अलग गति से एक ही दिशा में चलती हैं, तो वे 5 घंटे में मिलती हैं। यदि वे एक दूसरे की ओर यात्रा करती हैं, तो वे 1 घंटे में मिलती हैं। दोनों कारों की गति क्या है?

Ans: माना इकाई का अंक y है और दहाई का अंक x है। तब संख्या
10x+y है और
अंकों को उलटने पर प्राप्त संख्या = 10y + x
दिया है x + y =9........(i)
और 9 (10x + y) = 2(10y + x)
⇒ 90x + 9y = 20y + 2x
⇒ 88x - 11y = 0 ⇒ 8x - y = 0............(ii)
(i) और (ii) जोड़ने पर, हमें प्राप्त होता है
x + y + 8x - y = 9 + 0
⇒ 9x = 9 ⇒ x = 1
(i) में x का मान प्रतिस्थापित करने पर, हमें y=8 प्राप्त होता है
अत: संख्या 18 है।

47. y-अक्ष पर एक बिंदु खोजें जो बिंदु A(6, 5) और B(-4,3).

Ans: माना बिंदु (0, y) है
दोनों तरफ वर्ग करने पर, हमें प्राप्त होता है
36 + 25 + y² - 10y = 16 + 9 + y² – 6y
61 - 10y = 25 - 6y
10y - 6y = 61 - 25
4y = 36
⇒ y = 9
⇒ अभीष्ट बिंदु = (0, 9)