ISC Class 12 Maths Answer Key 2025 and Question Papers, Download PDF All SETs

SHARING IS CARING

If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

The ISC Class 12 Maths 2025 exam was conducted march 03, 2025. The exam lasted for 3 hours, was conducted from 2 PM to 5 PM, with an additional 15 minutes for reading the question paper.

The total marks allotted for the subject are 80 marks and divided into three sections with a total of 22 questions. Section A contained 14 questions, of which question 1 included sub-sections of 11 multiple-choice and 4 short answer questions, each carrying one mark.

Here we are providing a detailed analysis of student responses, expert opinions and the difficulty level of the paper including expected good scores, time-consuming section and longest question.

We have shared the ISC Class 12 Maths question paper 2025 PDF and answer key to help students check their answers and evaluate their performance.

👉 ISC Class 12 Maths Question Paper 2025, Download FREE PDF

ISC Mathematics Analysis 2025: Student Reactions

As the ISC Maths exam concludes at 5 pm, our experts will compile and share feedback and reactions from students who took the test, providing a comprehensive analysis of the exam below.

The paper had a mix of easy and tough questions.
Coordinate Geometry questions were a little challenging but doable.
The Vectors and Three-Dimensional Geometry questions were the easiest of all.
Questions were mostly expected, and from previous years.

ISC Class 12 Mathematics Exam Analysis 2025

To examine the performance and probable scores, students can check detailed Class 12 ISC Mathematics Exam Analysis 2025 comprising overall and section-wise difficulty level along with anticipated good attempts in the tabular format below-

Parameters	Analysis 2025
Overall difficulty level of the paper	Moderate
Difficulty level of Section A	Easy to Moderate
Difficulty level of Section B	Moderate
Difficulty level of Section C	Moderate
Overall expected good score	60+
Was the overall paper time-consuming?	No but the Calculus section was time-consuming.
Which section was the lengthiest?	Section C

ISC Class 12 Mathematics Answer Key 2025

Check the expert's answers for Question 1 comprising (i) to (xv) multiple-choice questions in the tabular format below.

Question

ISC Mathematics Answer Key 2025

(i) If A = then A ¹⁶is:
(a) Unit matrix
(b) Null matrix
(c) Diagonal matrix
(d) Skew matrix

(b) Null matrix

(ii) Which of the following is a homogeneous differential equation?
(a) (4x²+6y+5) dy - (3y² + 2x + 4) dx = 0
(b) (xy) dx(x³ + y³) dy = 0
(c) (x³ + 2y²) dx + 2xy dy = 0
(d) dy² dx + (x² - xy - y²) dy = 0

(d) dy² dx + (x² - xy - y²) dy = 0

(iii) Consider the graph of the function f(x) shown below:
Statement 1: The function f(x) is increasing in (2).
Statement 2: The function f(x) is strictly increasing in (2,1).
Which of the following is correct with respect to the above statements?
(a) Statement 1 is true and Statement 2 is false.
(b) Statement 2 is true and Statement 1 is false.
(c) Both the statements are true.
(d) Both the statements are false.

(iv)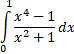

is equal to:
(a) 2/3
(b) 1/3
(c) -2/3
(d) 0

(v) Assertion: Consider the two events A and B such that n(A) = n(B), P(A/B) = P(B/A)
Reason: The events A and B are mutually exclusive.
(a) Both Assertion and Reason are true and Reason is the correct explanation for Assertion.
(b) Both Assertion and Reason are true but Reason is not the correct explanation for Assertion.
(c) Assertion is true and Reason is false.
(d) Assertion is false and Reason is true.

(vi) The existence of unique solution of the system of equations x + y = λ, 5x + ky = 2 depends on:
(a) λ only
(b) λ/k = 1
(c) both k and λ
(d) k only

(b) λ/k = 1

(vii) A cylindrical popcorn tub of radius 10 cm is being filled with popcorns at the of 314 cm³ per minute. The level of the popcorn in the tub is increasing at the of:
(a) 1 em/minute
(b) 0-1 cm/minute
(c) 1-1 cm/minute
(d) 0-5 cm/minute

(b) 0-1 cm/minute

(viii)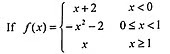

then the number of point (s) of discontinuity of f (x), is / are:
(a) 1
(b) 3
(c) 2
(d) 0

(a) 1

(ix) Assertion: If Set A has m elements, Set B has n elements and of one-one function(s) from AB is zero. then the number of one-one function(s) from A →B is zero.
Reason: A function f = A→B is defined only if all elements in Set A have an image Set B.

(a) Both Assertion and Reason are true and Reason is the correct explanation for Assertion
(b) Both Assertion and Reason are true but Reason is not the correct explanation for the Assertion
(c) Assertion is true and Reason is false
(d) Assertion is false and Reason is true

(b) Both Assertion and Reason are true but Reason is not the correct explanation for the Assertion

(x) Let X be a discrete random variable. The probability distribution of X is given below:

X	30	10	-10
P(X)	1/5	3/10	1/2

Then E(X) will be:
(a) 1
(b) 4
(c) 2
(d) 30

(d) 30

(xi) Statement 1: If A is an invertible matrix, then (A ²) ^-1= (A ^-1) ²
Statement 2: If A is an invertible matrix, then [A ^-1] = [A] ⁼¹
(a) Statement 1 is true and Statement 2 is false.
(b) Statement 2 is true and Statement 1 is false.
(c) Both the statements are true.
(d) Both the statements are false.