CBSE Class 12 Maths 2024-25: Chapter 12 Linear Programming Competency-Based Questions with Answers; Download Free PDF

As the CBSE Class 12 board exams get closer, students need to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.

This article explores Chapter 12 Linear Programming highlights key competency-based questions and provides answers to help students succeed.

Understanding Competency-Based Questions in Chapter 12 Linear Programming

Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.

These questions are different from regular memorization. They encourage students to think critically and solve problems, helping them better understand Chapter 12 Linear Programming concepts.

CBSE Class 12 Maths Chapter 12 Linear Programming Competency-Based Questions

Multiple Choice Questions

Q.1 Shown below is a linear programming problem (LPP).

Maximise Z = x + y

subject to the constraints:

x + y ≤ 1
-3 x + y ≥ 3
x ≥ 0
y ≥ 0

Which of the following is true about the feasible region of the above LPP?

1. It is bounded.
2. It is unbounded.
3. There is no feasible region for the given LPP.
4. (cannot conclude anything from the given LPP)

Answer. (3)

Q.2 Two statements are given below - one labelled Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).

Assertion ( A ): All the points in the feasible region of a linear programming problem are optimal solutions to the problem.

Reason ( R ): Every point in the feasible region satisfies all the constraints of a linear programming problem.

1. Both (A) and (R) are true and (R) is the correct explanation for (A).
2. Both (A) and (R) are true but (R) is not the correct explanation for (A).
3. (A) is false but (R) is true.
4. Both (A) and (R) are false.

Answer. (3)

Q: 3 Opticare Pvt. Ltd. is conducting an analysis of its operational costs, where labour cost is represented as x and the raw material is represented as y. The cost optimization was framed as a linear programming problem (LPP).

Observe the graph of the feasible region of the cost optimization LPP shaded below.

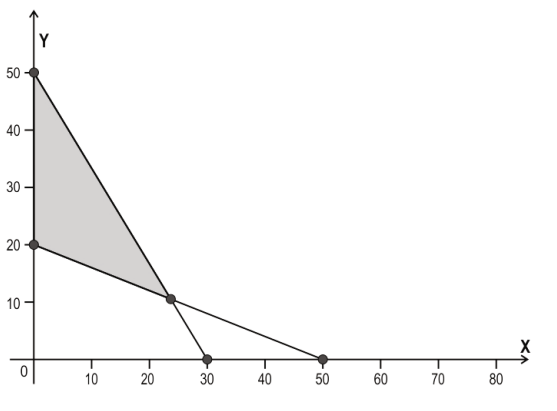
Which of the following inequalities is one of the constraints of the LPP?

1. 5x + 3y ≥ 150
2. 5y + 3 x 150
3. 2x+5y≥ 100
4. 2y+5x≤ 100

Answer. (3)

Q: 4 A linear programming problem (LPP) along with its constraints is given below.

Maximise Z = 2x + y

subject to the constraints:

x + 2 y ≤ 12
3x + y ≥ 3
x ≥ 0
y ≥ 0

Which option represents the feasible region of the above LPP?

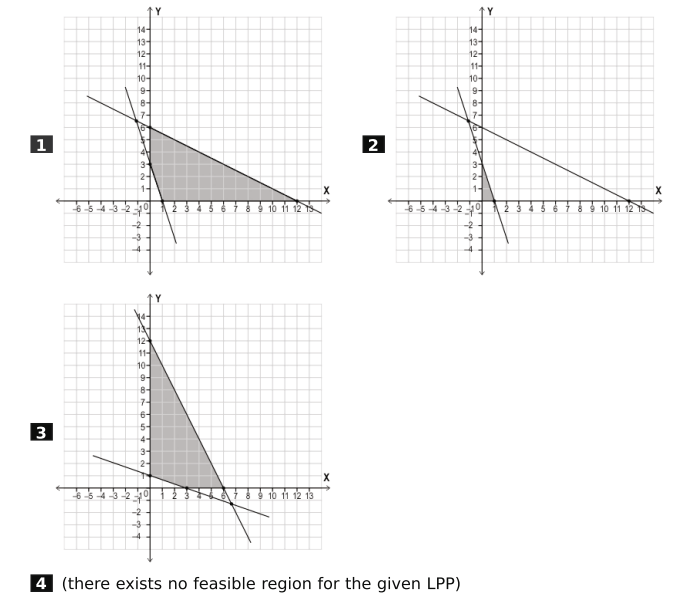
Answer. (1)

Download PDF
CBSE Class 12 Maths Chapter 1: Relations and Functions Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 2 : Inverse Trigonometric Functions Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 3 : Matrices Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 4: Determinants Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 5: Continuity & Differentiability Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 6: Application of Derivatives Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 7: Integrals Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 8: Application of Integrals Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 9: Differential Equations Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 10: Vector Algebra Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 11: Vector Algebra Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 11: Linear Programming Important Competency-Based Questions	Click Here

Q: 5 The objective function of a linear programming problem, along with its feasible region given below.

Z = 10 x + 3 y

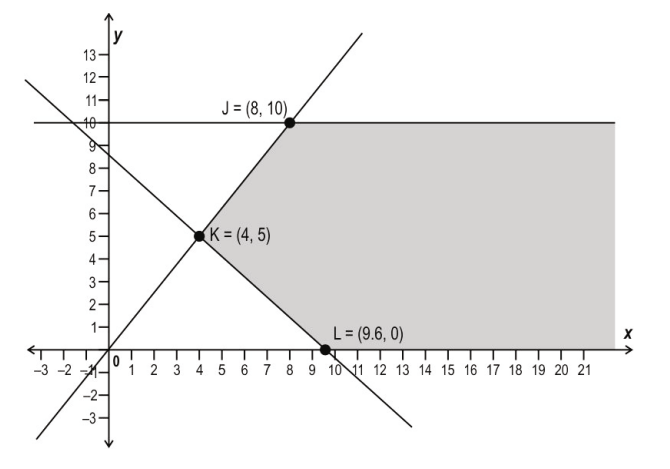
If J, K and L are the corner points, at which point does Z attain its minimum value?

1. Point J
2. Point K
3. Point L
4. (there exists no point at which Z attains its minimum value)

Answer. (2)

Q: 6 The objective function of a linear programming problem (LPP), Z = 4x + 3y, has to be minimised.

The feasible region of this LPP, along with its constraints, is shown in the graph below.

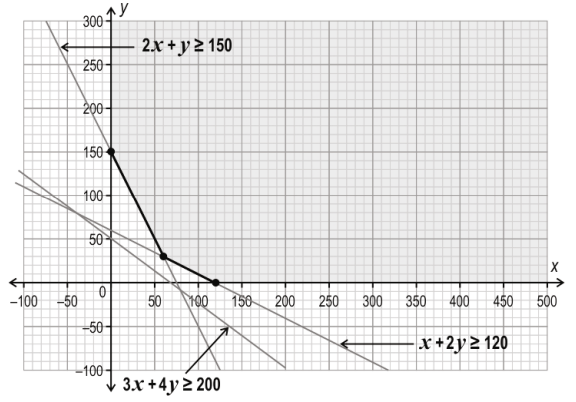
Which constraint, if removed, will not affect the feasible region?
1. x + 2y ≥ 120
2. 2 x + y ≥ 150
3. 3x + 4 y ≥ 200
4. (Any of the given constraints, if removed, will affect the feasible region.)

Answer. (3)

Free Response Questions

Q.7 Shown below is the feasible region of a linear programming problem(LPP) whose objective function is maximize Z = x + y.

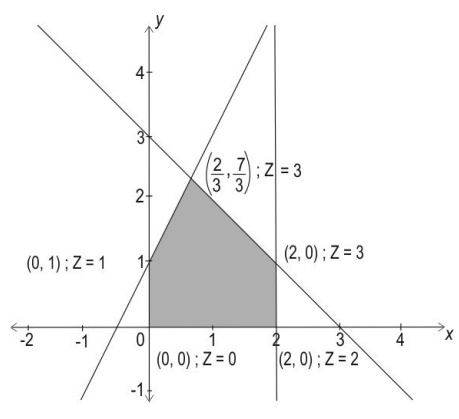
Sarla claimed that there exists no optimal solution for the LPP as there is no unique maximum value at the corner points of its feasible region.

Is her claim true? Give a valid reason.

Answer. Writes that Sarla's claim is false.

Q.8 State whether the following statement is true or false. Explain your reasoning.

In a linear programming problem, it is possible for a non-corner point to have the optimal value of the objective function, Z = a x + b y

Answer. Writes that the statement is true.

Gives a valid reason. For example, if two adjacent corner points yield the optimal value for the objective function, then every point on the line joining them also yields the optimal value.

Q.9 The shaded region in the graph shown below represents the feasible region for a linear programming problem with objective function Minimize: Z = 4 x - 3 y.

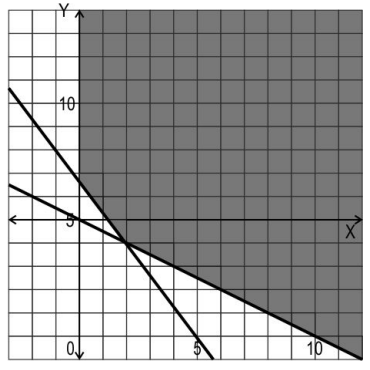
The values of the objective function at the corner points are given below:

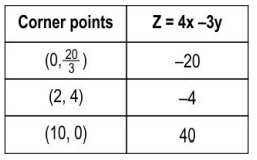
Suhas says that the minimum value of Z is (-20). Is he correct or incorrect? Justify your answer.

Answer. Writes that Suhas is incorrect.

Reasons that since the feasible area is unbounded, the minimum value of the objective function will exist only if the graph of 4 x - 3 y < (-20) has no point in common with the feasible region. Shows as an example that (1, 10) satisfies the inequality 4 x - 3 y < (-20) and is in common with the feasible region and hence, the minimum value of Z does not exist.

Q.10 A feasible region with respect to certain constraints is shaded in the graph below.

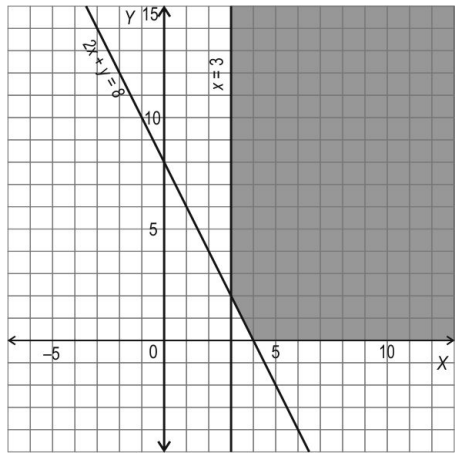
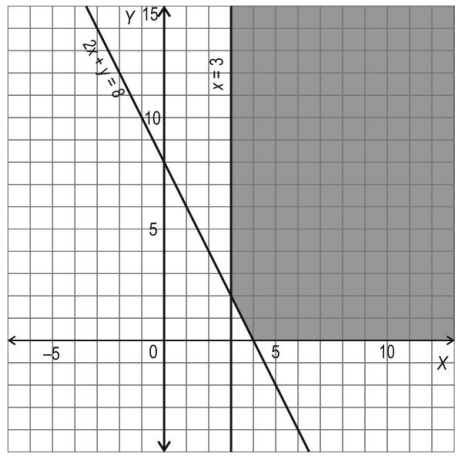
Reece says that the objective function Z = x + y will give an optimal solution when maximized. Is he correct or incorrect? Justify your answer.

Answer. Writes that he is incorrect.

Finds the value of the objective function at the corner points (2, 3) and (4, 0) as 5 and 4 respectively, and writes that x + y > 5 is overlapping with the feasible region and hence, no maximum value exists.

Q: 11 State whether the following statement is true or false. Justify your answer.

A linear programming problem can have infinitely many optimal solutions.

Answer. Writes true.

Justifies that in certain linear programming problems, the maximum/minimum value is obtained at 2 distinct corner points of the feasible region. In such cases, every point on the line joining those two points will be an optimal solution. Hence, a linear programming problem can have infinitely many optimal solutions.

(Award full marks for any equivalent justification.)

Q: 12 State whether the following statement is true or false. Justify your answer.

A linear programming problem whose feasible region is unbounded does not have an optimal solution.

Answer. Writes False(F).

Writes that, if on graphing the objective function, the open half-plane does not have any points common with the feasible region then the linear programming problem has an optimal solution.

Case Study

Answer the questions based on the given information.

Star Auto Private Limited (SAPL), an automobile company, manufactures and supplies precision machine components. Among other products, two products manufactured by SAPL are - Roller Bush and Hydraulic Valve shown below. These products are manufactured and packed in boxes of 25.

Each box of Roller Bush requires 2 kg of aluminium and 1 kg of steel. Each box of Hydraulic Valve requires 14 kg of aluminium and 2 kg of steel. SAPL has an available supply of 70 kg of aluminium and 20 kg of steel per day to manufacture these two products. The plant makes a profit of Rs 20 on each box of Roller Bush and Rs 50 on each box of Hydraulic Valve.

Q: 13 Write the mathematical formulation of the given scenario that gives the number of units of Roller Bush and Hydraulic Valve that SAPL must manufacture in order to maximize its profit.

Answer. Assumes the number of units of Roller Bush and Hydraulic Valve to be manufactured as x and y respectively and writes the mathematical formulation of the above scenario as:

Maximise Z = 20 x + 50 y

Subject to constraints:

2 x + 14 y ≤ 70
x + 2 y ≤ 20
X≥ 0
y ≥ 0

Q: 14 Determine the feasible region of the linear programming problem defined by the above scenario graphically.

Answer. Plots the graph of the constraints and shades the feasible region as follows:

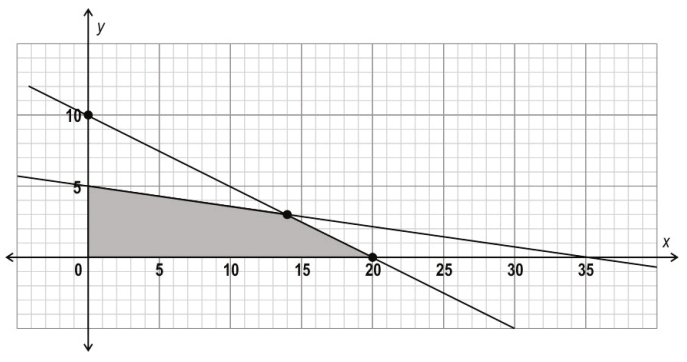
(Award only 1 mark if the constraints are plotted correctly but feasible region is not shaded/shaded incorrectly.)

Q: 15 Determine the number of units of Roller Bush and Hydraulic Valve that SAPL must manufacture in order to maximise its profit. Show your work.

Answer. Identifies the corner points and evaluates the value of Z at those points as follows:

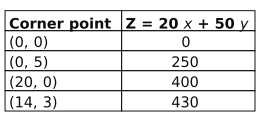
Writes that 430 is the largest value of Z and is obtained at (14, 3).

Concludes that 14 units of Roller Bush and 3 units of Hydraulic Valve must be manufactured by SAPL in order to maximize its profit.

👉 CBSE Class 12 Study Materials

CBSE Class 12 Syllabus 2024-25	CBSE Class 12 Previous Year Papers
NCERT Books For Class 12 Books	NCERT Class 12 Solutions
CBSE Class 12 Full Study Material	CBSE Class 12 Sample Paper 2024-25