CBSE Class 12 Maths 2024-25: Chapter 13 Probability Competency-Based Questions with Answers; Download Free PDF

As the CBSE Class 12 board exams get closer, students need to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.

This article explores Chapter 13 Probability highlights key competency-based questions and provides answers to help students succeed.

Understanding Competency-Based Questions in Chapter 13 Probability

Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.

These questions are different from regular memorization. They encourage students to think critically and solve problems, helping them better understand Chapter 13 Probability concepts.

CBSE Class 12 Maths Chapter 13 Probability Competency-Based Questions

Q: 1 Which of the following represents a Bernoulli trial?

1. Tossing a coin until a tail is obtained.
2. Recording eye colours found in a group of 500 people.
3. Asking a random sample of 50 people if they have ever been to Germany.
4. A bag contains 8 red marbles and 5 blue marbles. A marble is picked from the bag 5 times without replacement.

Answer. (3)

Q: 2 Study the following experiments.
Experiment 1:
A fair coin is flipped 7 times with the objective of getting heads each time. The outcome is heads 5 times out of 7.
Experiment 2:
A pen is selected at random from a box 4 times with the objective of getting a red pen. The box contains 2 blue, 2 red and 2 black pens and the selected pen is replaced after each trial.
In which experiment(s) is/are the trials Bernoulli trials?

1. Experiment 1
2. Experiment 2
3. both Experiment 1 and Experiment 2
4. Neither Experiment 1 nor Experiment 2

Answer. (3)

Q.3

Answer. (2)

Download PDF
CBSE Class 12 Maths Chapter 1: Relations and Functions Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 2 : Inverse Trigonometric Functions Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 3 : Matrices Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 4: Determinants Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 5: Continuity & Differentiability Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 6: Application of Derivatives Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 7: Integrals Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 8: Application of Integrals Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 9: Differential Equations Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 10: Vector Algebra Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 11: Vector Algebra Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 12: Linear Programming Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 13: Probability Important Competency-Based Questions	Click Here

Q: 4 A dog has six puppies. Assume that each puppy is equally likely to be a male or a female puppy.

What is the probability that the dog has exactly 4 female puppies?

Answer. (2)

Q: 5 Which of the following statements is true?

Answer. (3)

Q: 6 Which of the following is the probability of the seat being a side berth as well as a lower berth?

Answer. (1)

Q: 7 Which of the following is the probability of Raj getting an upper berth as well as a side berth?

Answer. (1)

Q: 8 Which of the following is the probability of Raj getting a side berth given that he has got an upper berth?

Answer. (2)

Q: 9 X and Y are the two events such that P(XY) = 0.2 and P(Y) = 0.5.

Find the value of P(X' n Y). Show your steps.

Answer. Writes that P(X' n Y) = P(X'|Y) × P(Y).

Uses the property of conditional probability and simplifies the above equation as:
P(X' n Y) = [1 - P(XY)] × P(Y)

Substitutes the given values in the above equation to find P(X' n Y) as:
P(X' n Y) = 0.8 x 0.5 = 0.4

Q: 10 Sukriti is playing a game with 16 identical white balls such that she can paint them as many times as she wants. She has the same set of balls in both the rounds. In the first round, she randomly spray paints 4 balls green. In the second round, she randomly spray paints 8 balls green.

At the end of the second round, what is the probability that a ball chosen at random is white? Show your steps.

Answer.

Q: 11 If a patient is selected at random, find the probability that he/she DOES NOT have migraine given that he/she has fever. Show your work.

Answer. Assumes the set of patients having fever and migraine to be F and M respectively.

Finds the required probability as:

P(M'|F) = 1 - P(M/F)

Q: 12 If a patient is selected at random, what is the probability that he/she has cold or fever or both, given that he/she has migraine? Show your work.

Answer. Assumes the set of patients having cold, fever and migraine to be C, F and M respectively.

Writes that the required probability is given by,

P(CUF❘M) = P(CM) + P(FM) - P(CnF|M)

Finds the probability that a patient selected at random has cold or fever, provided he/she has migraine as:

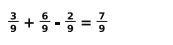
(Award 1.5 marks if the problem is solved correctly without explicitly writing the formula in step 1.)

Q.13 A and B are events in the sample space S such that P(A) > 0 and P(B) > 0.

Check whether the following statement is true or false. If true, justify your conclusion; if false, state the right expression.

“If A and B are mutually exclusive, the probability of at least one of them occurring is: P(A).P(B)”

Answer. Writes false.

Writes the correct expression. For example, since A and B are mutually exclusive, A ∩ B = Φ, which means that P(A ∩ B) = 0. Hence, the probability that at least one of them occurs is P(A ∪ B) = P(A) + P(B).

(Award full marks if just P(A ∪ B) = P(A) + P(B) is written without any explanation.)

Q.14 A survey says that approximately 30% of all products ordered online across various e-commerce websites are returned. Two products that are ordered online are selected at random.

If X represents the number of products that are returned,

i) find the probability distribution of X.

ii) find the mean or expectation of X. Show your work.

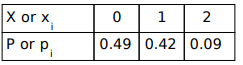
Answer. i) Writes that the possible values of X are 0, 1 and 2. Takes R to be the event that the product is returned and N to be the event that the product is not returned.

Uses the given information and finds the probability that the product is returned as P(R) = 0.3 and the probability that the product is not returned as P(N) = 1 - 0.3 = 0.7.

Finds the probability of each possible values of the random variable X as:

2 P(X = 0) = P(NN) = (0.7)(0.7) = 0.49

P(X = 1) = P(RN, NR) = (0.3)(0.7) + (0.7)(0.3) = 0.21 + 0.21 = 0.42

P(X = 2) = P(RR) = (0.3)(0.3) = 0.09

Finds the probability distribution of X as:

ii) Finds the mean or expectation of X as:

E(X) = ∑x_ip_i= (0 × 0.49) + (1 × 0.42) + (2 × 0.09) = 0.6

Q.15 Akshay is solving an exam paper with 50 multiple choice questions, each for 1 mark. In the paper, each multiple choice question has 4 options and exactly one correct answer.

Akshay solves only 30 questions, and randomly guesses the answers for the rest.

If exactly 40% of the questions Akshay solved are solved correctly, then what is the probability that Akshay scores at least 30 marks on the exam? Show your work.

Answer. Finds the number of questions Akshay solved correctly as 40% of 30 = 12.

Finds the number of questions Akshay randomly guessed the answer for as 20.

∴ The number of trials, n = 20

Assumes p as the probability that the answer is correct, and q as the probability that the answer is incorrect.

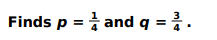
Finds that the required probability, P(at least 30 marks) = P(at least 18 correct guesses) = P(exactly 18 correct guesses) + P(exactly 19 correct guesses) + P(exactly 20 correct guesses).

Evaluates this using the Binomial Distribution as follows:

👉 CBSE Class 12 Study Materials

CBSE Class 12 Syllabus 2024-25	CBSE Class 12 Previous Year Papers
NCERT Books For Class 12 Books	NCERT Class 12 Solutions
CBSE Class 12 Full Study Material	CBSE Class 12 Sample Paper 2024-25