CBSE Class 12 Maths 2024-25: Chapter 5 Continuity & Differentiability Important Competency-Based Questions with Answers; Download Free PDF

As the CBSE Class 12 board exams get closer, students need to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.

This article explores Chapter 5 Continuity & Differentiability highlights key competency-based questions and provides answers to help students succeed.

Understanding Competency-Based Questions in Chapter 5 Continuity & Differentiability

Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.

These questions are different from regular memorization. They encourage students to think critically and solve problems, helping them understand the concepts in Chapter 5 Continuity & Differentiability better.

CBSE Class 12 Maths Chapter 5 Continuity & Differentiability Important Competency-Based Questions

Q.1 Shown below are the graphs of two functions.

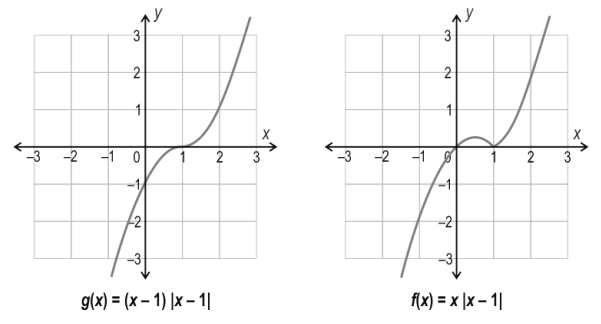
What can one conclude from the above graphs?

1. Product of a differentiable function and a non-differentiable function is ALWAYS differentiable.
2. Product of a differentiable function and a non-differentiable function is ALWAYS NOT differentiable.
3. Product of a differentiable function and a non-differentiable function MAY BE differentiable.
4. (cannot conclude anything from the given graphs.)

Answer. 3

Q.2 For what real value of a, is the function given below continuous for x E (-∞, +∞)?

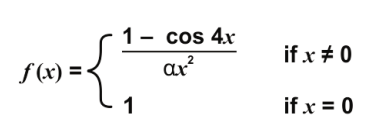
1. 2
2. 4
3. 8
4. (such a value of a does not exist)

Answer. 3

Q: 3 Which of the following is INCORRECT about a function f : R -> R?

1. If f is differentiable at x = c, then f is continuous at x = c.
2. If f is not differentiable at x = c, then f is not continuous at x = c.
3. If f is not continuous at x = c, then f is not differentiable at x = c.
4. If f is continuous at x = c, then f may or may not be differentiable at x = c.

Answer. 2

Q: 4 In which of these sets is the function f ( x ) = x | x - 22 differentiable twice?

1. R
2. R - {2}
3. R - {0, 2}
4. (the function cannot be differentiated twice in R)

Answer. 1

Q.5 The function f : R -> R is defined by:

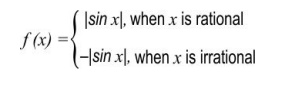
Read the statements carefully and then choose the option that correctly describes them.

Statement 1 : f ( x ) is continuous at x = 0.
Statement 2 : f ( x ) is discontinuous for all x ∈ R - {0}.

1. Statement 1 is true but Statement 2 is false.
2. Statement 1 is false but Statement 2 is true.
3. Both Statement 1 and Statement 2 are true.
4. Both Statement 1 and Statement 2 are false.

Answer. 4

Download PDF
CBSE Class 12 Maths Chapter 1: Relations and Functions Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 2 : Inverse Trigonometric Functions Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 3 : Matrices Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 4: Determinants Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 5: Continuity & Differentiability Important Competency-Based Questions	Click Here

Q.6 The Signum function f : R -> R, defined below, is discontinuous at x = 0. The identity function g : R -> R, defined below, is continuous everywhere.

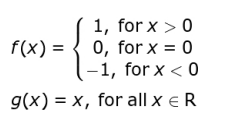
Which of these is true about the product of two functions ( f . g )?

1. ( f.g ) is discontinuous at x = 0 but continuous elsewhere in R.
2. ( f.g ) is not differentiable anywhere in R.
3. ( f.g ) is differentiable everywhere in R.
4. ( f.g ) is continuous everywhere in R.

Answer. 4

Q.7 Look at an inverse function below.

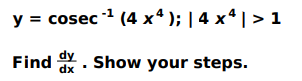
Answer. Differentiates the given function as:

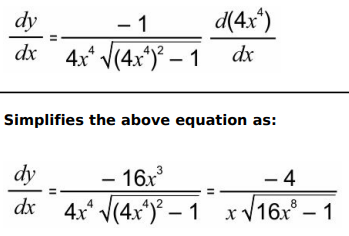
Q.8 Shown below are the graphs of two functions y = cos^-1 x and y = [cos ^-1 x ], where [cos ^-1 x ] denotes the greatest integer function.

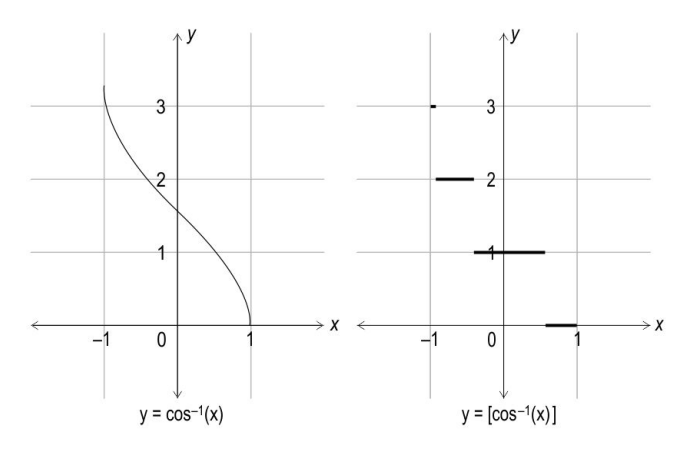
Find the points of discontinuity of the function y = [cos^-1 x ]. Show your work.

Answer. With the help of the graphs, finds the values of x for which cos 1.5 -1 x attains integer values as:

cos ^-1 x = 3
=> x = cos 3

cos ^-1 x = 2
=> x = cos 2

cos ^-1 x = 1
=> x = cos 1

Concludes that the points of discontinuity of the function y = [cos 0.5^-1 x ] are cos 3, cos 2 and cos 1.

Q.9

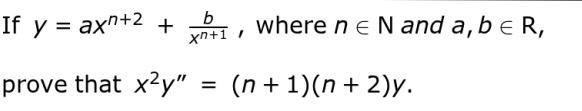
Answer. Finds the first derivative of y as:

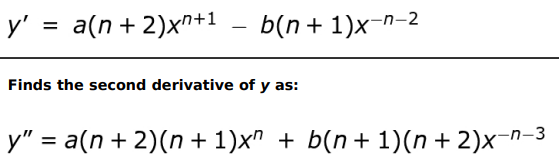
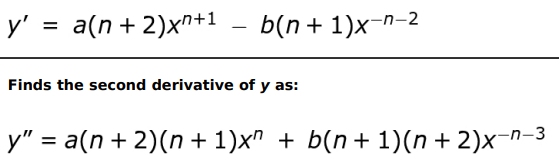
Q.10 Find the value of ( f o g )' at x = 4 if f ( u ) = u ³ + 1 and u = g ( x ) = √ x. Show your work.

Answer. Finds ( f o g )( x ) as:

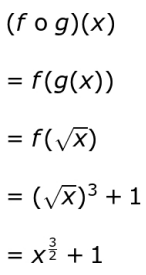
Finds the derivative of ( f o g )( x ) as:

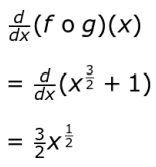
Uses the above step to find the value of ( f o g )' at x = 4 as 3.

Q.11

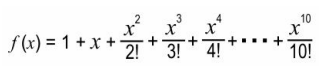
If f ( x ) is differentiated successively 10 times, what is f (10) ( x )? Show your work.

Answer. Differentiates f ( x ) once to get:

(Award full marks if the expression is correctly generalised at the second derivative stage.)
Finds the value of f 0.5 ⁽¹⁰⁾ ( x ) as f ⁽¹⁰⁾ = 1.

Q.12

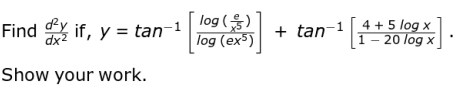
Answer.

Simplifies above step to get:
y = tan -1 1 + tan -1 4

Differentiates the above equation to get y' = 0.
Differentiates y' to get y '' = 0.

Q.13

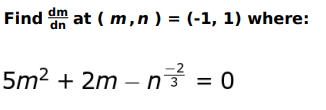
Answer. Differentiates the equation given in the question with respect to n as follows:

Simplifies the previous step as:

Case Study

Answer the questions based on the information given below.

Ambika, a mathematics teacher is conducting a practice session on calculus where she is discussing continuity and differentiability of several functions in their domains. Shown below are four cards that contain a function each along with their domains and graphs.

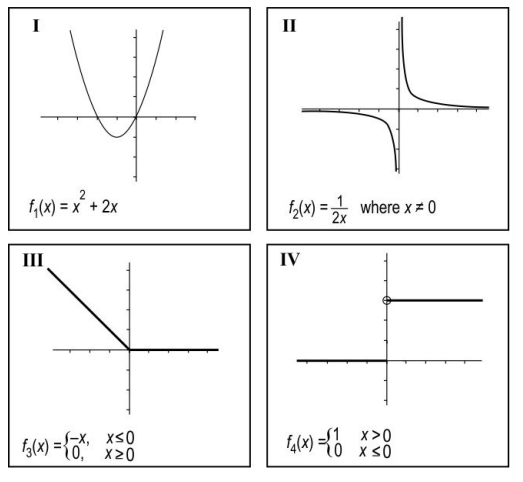
While discussing in the group, four students claimed as follows:

♦ Leela: "As the function on card I is both continuous and differentiable, we can say that every continuous function is differentiable."
♦ Irfan: "As the graph is not in one piece, the function on card II is discontinuous."
♦ Deepak: "The function on card III is continuous."
♦ Kiran: "The function on card IV is discontinuous."

Answer.

Q.14 Check whether Deepak and Kiran's claims are correct. Justify your answer.

Answer. Writes that Deepak is right and justifies it as follows

As f ₃ (x) satisfies all the 3 conditions given below, it is continuous.

♦ f ₃ ( x ) is defined for all real numbers.
♦ At x = 0, left hand limit = right hand limit = 0
♦ f (0) = 0

Writes that Kiran is right and justifies it as follows:

As f ₄ ( x ) fails to satisfy that at x = 0, left hand limit (0) is not equal to the right hand limit (1), it is discontinuous.

Q.15 Is Leela's claim true for all continuous functions? Justify with a valid reason or provide a counterexample.

The table below gives the correct answer for each multiple-choice question in this test.

Answer. Writes that Leela's claim is not true for all continuous functions

Gives an example. Foe example: f₃ ( x ) is continuous, but not differentiable as it it has a corner point. (Award full marks if any other valid examples are given.)

----

👉 CBSE Class 12 Study Materials

CBSE Class 12 Syllabus 2024-25	CBSE Class 12 Previous Year Papers
NCERT Books For Class 12 Books	NCERT Class 12 Solutions
CBSE Class 12 Full Study Material	CBSE Class 12 Sample Paper 2023-24