CBSE Class 12 Maths 2024-25: Chapter 6 Applications of Derivatives Important Competency-Based Questions with Answers; Download Free PDF

As the CBSE Class 12 board exams get closer, students need to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.

This article explores Chapter 6 Applications of Derivatives highlights key competency-based questions and provides answers to help students succeed.

Understanding Competency-Based Questions in Chapter 6 Applications of Derivatives

Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.

These questions are different from regular memorization. They encourage students to think critically and solve problems, helping them understand the concepts in Chapter 6 Applications of Derivatives better.

CBSE Class 12 Maths Chapter 6 Applications of Derivatives Important Competency-Based Questions

Q.1 The sub-tangent of a curve at a point is the projection on the x -axis of the portion of the tangent to the curve between the x -axis and the point of tangency. The sub-tangent of a curve y = f (x) at a point P( x_o ,y_o ) is illustrated below.

Answer.

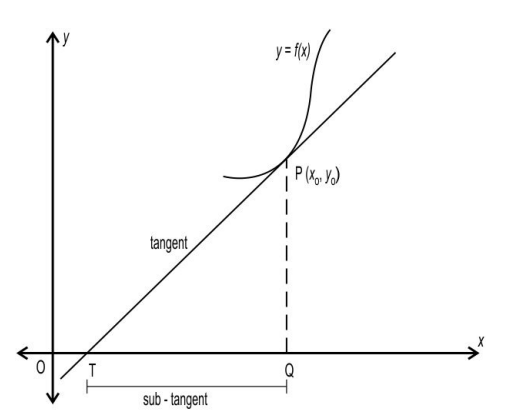
Among the given slopes of tangents of a curve at a given point, which will result in the longest sub-tangent?

1. 30°
2. 45°
3. 60°
4. 90°

Answer. (1)

Q: 2 The diagonal of a square, of side 3√2 cm, is increasing at a rate of 2 cm/s.

Which of the following is the rate at which its area is increasing?

1. √2 cm²/s
3. 12 cm²/s
2. 6√2 cm²/s
4. 24 cm²/s

Answer. (3)

Q: 3 Sameer wants to find the area of his garden. He measures the side of his square garden as 10 m with an error of 0.05 m.

Which of the following is the approximate error that Sam will have in calculating its area?

1. 0.05 m²
2. 0.5 m²
3. 1 m²
4. 10.05 m²

Answer. (3)

Q: 4 Gagan wants to calculate the capacity of a cylindrical water tank. He precisely measures the height of the tank as 7 m. Next, he measures the radius of the tank as 2 m, with an error of 0.05 m. The error occured while measuring the radius results in an error in calculating the capacity.

What is the approximate error in calculating the capacity of the water tank?

1. 2.2 m³
2. 2. 4.4 m³
3. 44 m³
4. 88 m³

Answer. (2)

Q: 5 Study the function below.

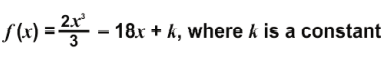
Which of the following is true about the nature of the function in the interval [-3, 3]?

1. f(x) is increasing
2. f(x) is decreasing
3. f(x) is neither increasing nor decreasing
4. (cannot say without knowing the value of k )

Answer. (2)

Download PDF
CBSE Class 12 Maths Chapter 1: Relations and Functions Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 2 : Inverse Trigonometric Functions Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 3 : Matrices Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 4: Determinants Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 5: Continuity & Differentiability Important Competency-Based Questions	Click Here
CBSE Class 12 Maths Chapter 6: Application of Derivatives Important Competency-Based Questions	Click Here

Q: 6 The normal to the curve y = f ( x ) at the point (5, 7) makes an angle of π/4 with the x -axis in the positive direction.

Find f'(5). Show your work.

Answer.

Q: 7 Aditi is making a circular dosa. She is spreading the dosa batter such that its radius is increasing at a rate of 2 cm/s.

Find the rate of change of the area of the dosa, in terms of π, when its radius is 9 cm. Show your steps.

Answer. Finds the expression for the rate of change of the area of the dosa as:

Q.8

Answer.

Q.9

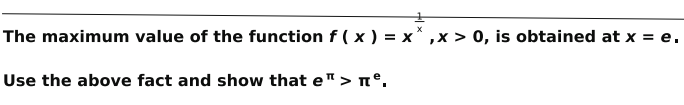
Answer. Writes that, as the maximum value of f ( x ) is obtained at x = e, f (e) > f ( x ), for every x > 0.

Uses the above step to write:

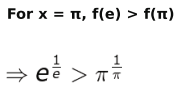
Raises the power on both sides of the above inequality by (e π) and simplifies the same to get:

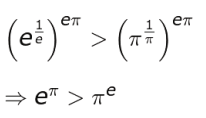
Q: 10 A circular metallic plate is expanding such that its area is constantly increasing with respect to time.

Milind claims that the rate of increase of its perimeter with respect to time is inversely proportional to its radius.

Is Milind's claim correct? Justify your answer.

Answer. Finds the rate of change of area of the circular plate with respect to time and equates it to a constant k as:

Q: 11 A particle is moving such that its distance s from a fixed point at any time t is given by
s = Asin t + Bcos t, where A, B ∈ R.

Show that the particle's acceleration is always numerically equal to its distance from the fixed point.

Answer. Differentiates s to find velocity as:
s' = Acos t - Bsin t

Differentiates s' to find acceleration as:
s" -Asin t - Bcos t

Rewrites acceleration in terms of distance as s" = (-s) and writes that the
magnitudes of distance and acceleration are the same.

Hence, concludes that acceleration is always numerically equal to the distance of the particle from the fixed point.

Q: 12 A solid sphere of gold, of radius 5 cm, is being melted in a furnace such that the radius is decreasing uniformly.

When its radius is 1 cm, show that the rate at which its surface area is decreasing with respect to time is twice the rate at which its volume is decreasing with respect to time.

Answer.

Q: 13 A basketball has a tiny hole that leads to it getting deflated while maintaining a spherical shape.

Find the ratio of the rate of loss of the volume of air to the rate of loss of the surface area of the ball when the radius of the ball is 8 cm. Show your steps.

Answer.

Q: 14 A cylindrical disk of radius R and height H is pressed by a hydraulic press. During the process, the radius and the height of the disk change such that the cylindrical shape is retained and the volume of the disk remains constant.

What is the ratio of the rate of change of height to the rate of change of radius in terms of R? Show your steps and give valid reasons.

Answer.

Q: 15 Simran cuts a metallic wire of length a m into two pieces. She uses both pieces to create two squares of different side lengths.

Find the side lengths of the squares (in terms of a ) for which the combined area will be MINIMUM? Show your steps and give reasons.

Answer.

----

👉 CBSE Class 12 Study Materials

CBSE Class 12 Syllabus 2024-25	CBSE Class 12 Previous Year Papers
NCERT Books For Class 12 Books	NCERT Class 12 Solutions
CBSE Class 12 Full Study Material	CBSE Class 12 Sample Paper 2023-24