CBSE Class 12 Maths 2024-25: Chapter 11 Three Dimensional Geometry Competency-Based Questions with Answers; Download Free PDF

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
As the CBSE Class 12 board exams get closer, students need to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.
This article explores Chapter 11 Three Dimensional Geometry highlights key competency-based questions and provides answers to help students succeed.
Understanding Competency-Based Questions in Chapter 11 Three Dimensional Geometry
Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.
These questions are different from regular memorization. They encourage students to think critically and solve problems, helping them better understand Chapter 11 Three Dimensional Geometry concepts.
CBSE Class 12 Maths Chapter 11 Three Dimensional Geometry Competency-Based Questions
Multiple Choice Questions
Q.1 Given below are the vector equations of two planes.
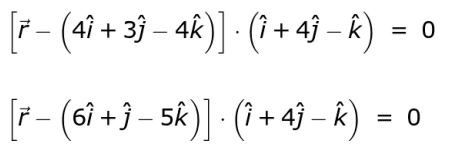
Which of the following is true about these planes?
1. They coincide with each other.
2. They are parallel to each other.
3. They are perpendicular to each other.
4. They are not perpendicular but intersect each other along a unique line.
Answer. (2)
Q.2 Shown below are equations of four planes.
P1 : -2 x - 3 y - 4 z - 20 = 0
P2 : 2x + 3y + 4z - 9 = 0
P3 : -4 x - 6 y + 8 z = 0
P4 : 4 x + 6 y + 8 z = 0
Which of the provided planes does NOT share parallelism with the rest?
1. P 1
2. P 2
3. P 3
4. P 4
Answer. (3)
Q: 3 A line passes through (2, -1, -3) and (0, 2, 3).
Which of the following are the direction cosines of a line parallel to the given line at a distance of 3 units from the given line?
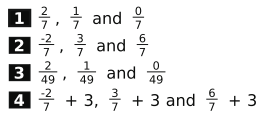
Answer. (2)
Q: 4 The direction ratios of two parallel lines are 3,λ , (-10) and (-5), 7, δ respectively. Which of the following are the values of λ and δ ?

Answer. (3)
| Download PDF | |
| CBSE Class 12 Maths Chapter 1: Relations and Functions Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 2 : Inverse Trigonometric Functions Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 3 : Matrices Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 4: Determinants Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 5: Continuity & Differentiability Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 6: Application of Derivatives Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 7: Integrals Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 8: Application of Integrals Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 9: Differential Equations Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 10: Vector Algebra Important Competency-Based Questions | Click Here |
| CBSE Class 12 Maths Chapter 11: Vector Algebra Important Competency-Based Questions | Click Here |
Q: 5 Which of the following is the sum of the direction cosines of the y-axis?
1.0
2.1
3.80°
4.(cannot say without being given two points on the y-axis)
Answer. (2)
Free Response Questions
Q.6 There are three points P, Q and R. The direction ratios of line PQ are (-2), 1 and 3 and that of line QR are 6, (-3) and (-9).
Is there a unique plane that contains the points P, Q and R? Justify your answer.
Answer. Finds that the direction ratios of PQ and QR are proportional. The working may look 0.5 as follows:

States that there is no unique plane because P, Q and R are collinear and infinitely many planes that contain three collinear points exist.
Q.7 The equations for line m and line n are given below.

Answer. Since the two lines are perpendicular, writes the equation
3(2) + 2(1) + 2(- k ) = 0
Solves the above equation to find the value of k as 4.
Q.8 Line m and line n are two lines which are not parallel, and do not intersect each other.
Asha, Ravi and Saquib tried to find the shortest distance between lines m and n .
♦ Asha found a line k parallel to line m on the same plane as line n. She found the shortest distance as the distance between lines k and n .
♦ Ravi found the length of a line segment that is perpendicular to both line m and line n as the shortest distance.
♦ Saquib said that it is impossible to find the distance between the two lines, since the lines are not parallel, and do not intersect.
Which of them is/are using the correct approach? Justify your answer
Answer. Writes that only Ravi is using the correct approach. Gives a reason.
For example, lines m and n are skew lines, and the distance between skew lines is given by the length of a line segment that is perpendicular to both lines. Hence, Saquib is incorrect.
Asha is incorrect as the shortest distance between two non-parallel lines on the same plane is 0.
Q.9 Shown below are the equations of two planes.
P 1 : 3 x - 3 y - 3 z = 1
P 2 : -3 x + ny - z = 4
If P 1 is perpendicular to P 2 , find the value of n . Show your work.
Answer. Writes that since P1 is perpendicular to P2 , their normals are also perpendicular. Thus equates the dot product of the normals to zero and finds the value of n as (-2). The working may look as follows.
3(-3) + (-3) n + (-3)(-1) =
0 => -9 - 3n + 3 = 0
=> n = -2
Q.10

Find the value of G. Show your steps.
Answer. Writes the equation of the line in vector form as follows:

Case Study
Read the information given below and answer the questions that follow.
A supply ship left a port to replenish food and equipment for the Indian navy. Enemies used a submarine to track the ship and scout the port.
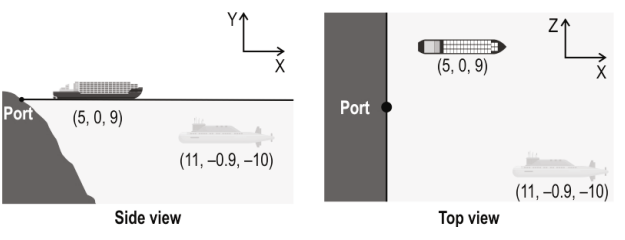
Assuming the port to be at the origin, the position of the ship is (5 km, 0 km, 9 km) and the position of the submarine is (11 km, -0.9 km, -10 km).
Q: 11 What angle does the line joining the ship and the port make with the z axis?

Answer. (3)
Q.12 Which of the following is the cartesian equation of the line joining the ship to the submarine?

Answer. (2)
Q: 13 The submarine squad wants to find the direction cosines of the line joining the submarine to the port.
The captain of the submarine says that the direction cosines are:
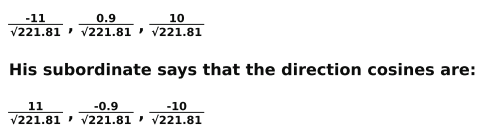
Who is correct?
1. The captain
2. The subordinate
3. Both of them
4. Neither of them
Answer. (3)
Q: 14 The distance between the port and the ship is √106 km, the distance between the submarine and the port is √221.81 km and the distance between the ship and the submarine is √397.81 km.
Which of the following represents the angle between the lines joining the submarine to the ship and the line joining the submarine to the port?

Answer. (3)
Q: 15 Which of the following is the equation of the line joining the submarine and the port?
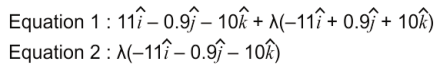
1. Equation 1
3. Both equation 1 and equation 2
2. Equation 2
4. Neither equation 1 nor equation 2
Answer. (1)
👉 Read Also - CBSE Class 12 Half-Yearly/Mid Term 2024-25 : Most Important Questions with Answers; PDF Download (All Subjects)
👉 Read Also - How CBSE’s New Exam Pattern Will Impact Class 11 and 12 Students
👉 CBSE Class 12 Study Materials
| CBSE Class 12 Syllabus 2024-25 | CBSE Class 12 Previous Year Papers |
| NCERT Books For Class 12 Books | NCERT Class 12 Solutions |
| CBSE Class 12 Full Study Material | CBSE Class 12 Sample Paper 2024-25 |







 Profile
Profile Signout
Signout












 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










